Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-19T15:05:01.169Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure of the 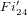$Fi_{24}^{\prime }$ maximal $2$-local geometry point-line collinearity graph

Part of: Structure and classification of infinite or finite groups Graph theory

Published online by Cambridge University Press:  01 March 2016

Peter Rowley  and
Ben Wright
Peter Rowley
Affiliation:
The School of Mathematics, Alan Turing Building, The University of Manchester, Oxford Road, Manchester M13 9PL, United Kingdom email peter.j.rowley@manchester.ac.uk
Ben Wright
Affiliation:
The School of Mathematics, Alan Turing Building, The University of Manchester, Oxford Road, Manchester M13 9PL, United Kingdom email ben.t.wright@gmail.com

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The point-line collinearity graph 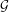${\mathcal{G}}$ of the maximal 2-local geometry for the largest simple Fischer group, 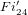$Fi_{24}^{\prime }$, is extensively analysed. For an arbitrary vertex $a$ of 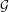${\mathcal{G}}$, the 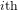$i\text{th}$-disc of $a$ is described in detail. As a consequence, it follows that 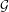${\mathcal{G}}$ has diameter $5$. The collapsed adjacency matrix of 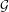${\mathcal{G}}$ is given as well as accompanying computer files which contain a wealth of data about 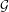${\mathcal{G}}$.

Supplementary materials are available with this article.

MSC classification

Primary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.) 20E32: Simple groups
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Issue 1 , 2016 , pp. 105 - 154
Copyright
© The Author(s) 2016 

References

Buekenhout, F., ‘The geometry of diagrams’, Geom. Dedicata 8 (1979) 253–257.CrossRefGoogle Scholar
Buekenhout, F., ‘Diagrams for geometries and groups’, J. Combin. Theory Ser. A 27 (1979) 121–151.CrossRefGoogle Scholar
Buekenhout, F., ‘Finite groups and geometries: a view on the present state and on the future’, Groups of Lie type and their geometries (Como, 1993) , London Mathematical Society Lecture Note Series 207 (Cambridge University Press, Cambridge, 1995) 35–42.CrossRefGoogle Scholar
Buekenhout, F., Dehon, M. and Leemans, D., ‘An atlas of residually weakly primitive geometries for small groups’, Acad. Roy. Belg. Cl. Sci. Mém. Collect. 8 14 (1999) no. 3.Google Scholar
Cannon, J. J. and Playoust, C., An introduction to algebraic programming with Magma (Springer, 1997).Google Scholar
Conway, J. H., Curtis, R. T., Norton, S. P., Parker, R. A. and Wilson, R. A., Atlas of finite groups (Clarendon Press, Oxford, 1985).Google Scholar
The GAP group, ‘GAP—Groups, algorithms, and programming, version 4.4’, 2005,http://www.gap-system.org.Google Scholar
J. I., Hall and Shpectorov, S. V., ‘A characterization of the P-geometry for M 23 ’, Adv. Geom. 5 (2005) no. 3, 421–430.Google Scholar
Ivanov, A. A., ‘A geometric characterization of the Monster’, Groups, combinatorics and geometry (Durham, 1990) , London Mathematical Society Lecture Note Series 165 (Cambridge University Press, Cambridge, 1992) 46–62.CrossRefGoogle Scholar
Ivanov, A. A., ‘Geometric approach to the problem of uniqueness for sporadic simple groups’, Dokl. Akad. Nauk SSSR 316 (1991) no. 5, 1043–1046; (in Russian); translation in Soviet Math. Dokl. 43 (1991), no. 1, 226–229.Google Scholar
Ivanov, A. A., Geometry of sporadic groups. I. Petersen and tilde geometries , Encyclopedia of Mathematics and its Applications 76 (Cambridge University Press, Cambridge, 1999).CrossRefGoogle Scholar
Ivanov, A. A. and Shpectorov, S. V., ‘Geometries for sporadic groups related to the Petersen graph. I’, Comm. Algebra 16 (1988) no. 5, 925–953.CrossRefGoogle Scholar
Ivanov, A. A. and Shpectorov, S. V., ‘Geometries for sporadic groups related to the Petersen graph. II’, European J. Combin. 10 (1989) no. 4, 347–361.CrossRefGoogle Scholar
Ivanov, A. A. and Shpectorov, S. V., ‘ P-geometries of J 4 -type have no natural representations. Algebra, groups and geometry’, Bull. Soc. Math. Belg. Ser. A 42 (1990) no. 3, 547–560.Google Scholar
Ivanov, A. A. and Shpectorov, S. V., ‘The flag-transitive tilde and Petersen-type geometries are all known’, Bull. Amer. Math. Soc. (N.S.) 31 (1994) no. 2, 173–184.CrossRefGoogle Scholar
Ivanov, A. A. and Shpectorov, S. V., Geometry of sporadic groups. II. Representations and amalgams , Encyclopedia of Mathematics and its Applications 91 (Cambridge University Press, Cambridge, 2002).CrossRefGoogle Scholar
Ivanov, A. A. and Wiedorn, C., ‘More on geometries of the Fischer group Fi 22 ’, J. Algebraic Combin. 16 (2002) no. 2, 111–150.CrossRefGoogle Scholar
Mason, G. and Smith, S. D., ‘Minimal 2-local geometries for the Held and Rudvalis sporadic groups’, J. Algebra 79 (1982) no. 2, Part 1, 286–306.CrossRefGoogle Scholar
Ronan, M. A. and Smith, S. D., ‘2-Local geometries for some sporadic groups’, Proc. Sympos. Pure Math. 37 (1980) 283–289.CrossRefGoogle Scholar
Ronan, M. A. and Stroth, G., ‘Minimal parabolic geometries for the sporadic groups’, European J. Combin. 5 (1984) no. 1, 59–91.CrossRefGoogle Scholar
Rowley, P., ‘On the minimal parabolic system related to M 24 ’, J. Lond. Math. Soc. (2) 40 (1989) no. 1, 40–56.CrossRefGoogle Scholar
Rowley, P., ‘On the minimal parabolic system related to the Monster simple group’, J. Combin. Theory Ser. A 96 (2001) no. 2, 199–260.CrossRefGoogle Scholar
Rowley, P., ‘A monster graph. I’, Proc. Lond. Math. Soc. (3) 90 (2005) no. 1, 42–60.CrossRefGoogle Scholar
Rowley, P. and Walker, L., ‘A note on the M 23 - and Fi 23 -minimal parabolic geometries’, Proc. Amer. Math. Soc. 121 (1994) no. 2, 317–322.Google Scholar
Rowley, P. and Walker, L., ‘A characterization of the Co2 -minimal parabolic geometry’, Nova J. Algebra Geom. 3 (1994) no. 2, 97–155.Google Scholar
Rowley, P. and Walker, L., ‘On the Fi 22 -minimal parabolic geometry’, Geom. Dedicata 61 (1996) no. 2, 121–167.CrossRefGoogle Scholar
Rowley, P. and Walker, L., ‘A 11,707,448,673,375 vertex graph related to the baby monster. I’, J. Combin. Theory Ser. A 107 (2004) no. 2, 181–213.CrossRefGoogle Scholar
Rowley, P. and Walker, L., ‘A 11,707,448,673,375 vertex graph related to the baby monster. II’, J. Combin. Theory Ser. A 107 (2004) no. 2, 215–261.CrossRefGoogle Scholar
Rowley, P. and Walker, L., ‘The maximal 2-local geometry for J 4 . I’, JP J. Algebra Number Theory Appl. 9 (2007) no. 2, 145–213.Google Scholar
Rowley, P. and Walker, L., ‘The maximal 2-local geometry for J 4 . II’, JP J. Algebra Number Theory Appl. 10 (2008) no. 1, 9–49.Google Scholar
Rowley, P. and Walker, L., ‘The maximal 2-local geometry for J 4 . III’, JP J. Algebra Number Theory Appl. 10 (2008) no. 2, 129–167.Google Scholar
Rowley, P. J. and Walker, L. A., ‘A 195, 747, 435 vertex graph related to the Fischer group Fi 23 I ’, JP J. Algebra Number Theory Appl. 23 (2011) no. 1, 87–129.Google Scholar
Rowley, P. J. and Walker, L. A., ‘Octad orbits for certain subgroups of $M_{24}$ ’, MIMS Preprint 2015.96.Google Scholar
Rowley, P. J. and Walker, L. A., ‘The point-line collinearity graph of the $Fi_{24}^{\prime }$ maximal $2$ -local geometry — the first three discs’, MIMS Preprint 2015.97.CrossRefGoogle Scholar
Segev, Y., ‘On the uniquenss of the Co 1  2-local geometry’, Geom. Dedicata 25 (1988) 159–219.CrossRefGoogle Scholar
Shpektorov, S. V., ‘Geometric characterization of the group M 22 ’, Investigations in the algebraic theory of combinatorial objects (Vsesoyuz. Nauchno-Issled. Inst. Sistem. Issled., Moscow, 1985) 112–123.Google Scholar
Shpectorov, S. V., ‘The universal 2-cover of the P-geometry G(Co2)’, European J. Combin. 13 (1992) no. 4, 291–312.CrossRefGoogle Scholar
Smith, S. D., ‘Residual geometries for sporadic and classical groups, a survey’, Finite groups, coming of age (Montreal, Quebec, 1982) , Contemporary Mathematics 45 (American Mathematical Society, Providence, RI, 1985) 315–334.CrossRefGoogle Scholar
Stroth, G., ‘Some geometry for McL’, Comm. Algebra 17 (1989) no. 11, 2825–2833.CrossRefGoogle Scholar
Stroth, G., ‘Some sporadic geometries’, Groups, difference sets, and the Monster (Columbus, OH, 1993) , Ohio State University Mathematical Research Institute Publications 4 (de Gruyter, Berlin, 1996) 99–116.CrossRefGoogle Scholar
Tits, J., Buildings of spherical type and finite BN-pairs , Lecture Notes in Mathematics 386 (Springer, Berlin–New York, 1974).Google Scholar
Tits, J., ‘A local approach to buildings’, The geometric vein (eds Davis, C., Grünbaum, B. and Sherk, F. A.; Springer, 1981) 517–522.Google Scholar
Weiss, R., ‘A geometric characterization of the groups McL and Co3 ’, J. Lond. Math. Soc. (2) 44 (1991) no. 2, 261–269.CrossRefGoogle Scholar
Weiss, R. and Yoshiara, S., ‘A geometric characterization of the groups Suz and HS’, J. Algebra 133 (1990) no. 1, 182–196.CrossRefGoogle Scholar
Yoshiara, S., ‘Some geometries for J 3 and O’N’, European J. Combin. 10 (1989) no. 5, 499–506.CrossRefGoogle Scholar
Supplementary material: File

Rowley and Wright supplementary material

Rowley and Wright supplementary material 1

Download Rowley and Wright supplementary material(File)
File 17.8 MB