Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-23T13:35:09.646Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffusive logistic equations with indefinite weights: population models in disrupted environments

Published online by Cambridge University Press:  14 November 2011

Robert Stephen Cantrell  and
Chris Cosner
Robert Stephen Cantrell
Affiliation:
Department of Mathematics and Computer Science, The University of Miami, Coral Gables, Florida 33124, U.S.A.
Chris Cosner
Affiliation:
Department of Mathematics and Computer Science, The University of Miami, Coral Gables, Florida 33124, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

The dynamics of a population inhabiting a strongly heterogeneous environment are modelledby diffusive logistic equations of the form ut = d Δu + [m(x) — cu]u in Ω × (0, ∞), where u represents the population density, c, d > 0 are constants describing the limiting effects of crowding and the diffusion rate of the population, respectively, and m(x) describes the local growth rate of the population. If the environment ∞ is bounded and is surrounded by uninhabitable regions, then u = 0 on ∂∞× (0, ∞). The growth rate m(x) is positive on favourablehabitats and negative on unfavourable ones. The object of the analysis is to determine how the spatial arrangement of favourable and unfavourable habitats affects the population being modelled. 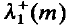The models are shown to possess a unique, stable, positive steady state (implying persistence for the population) provided l/d> where 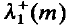is the principle positive eigenvalue for the problem — Δϕ=λm(x)ϕ in Χ,ϕ=0 on ∂Ω. Analysis of how 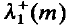depends on m indicates that environments with favourable and unfavourable habitats closely intermingled are worse for the population than those containing large regions of uniformly favourable habitat. In the limit as the diffusion rate d ↓ 0, the solutions tend toward the positive part of m(x)/c, and if m is discontinuous develop interior transition layers. The analysis uses bifurcation and continuation methods, the variational characterisation of eigenvalues, upper and lower solution techniques, and singular perturbation theory.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 112 , Issue 3-4 , 1989 , pp. 293 - 318
Copyright
Copyright © Royal Society of Edinburgh 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alexander, J. C. and Antman, S. S.. Global behavior of solutions of nonlinear equations depending on infinite-dimensional parameters. Indiana Univ. Math. J. 32 (1983), 39–62.CrossRefGoogle Scholar
2Amann, H., Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces. SIAM Rev. 18 (1976), 620–709.CrossRefGoogle Scholar
3Aronson, D. G., Ludwig, D. and Weinberger, H. F.. Spatial patterning of the spruce budworm. J. Math. Biol. 8 (1979), 217–258.Google Scholar
4Beltramo, A. and Hess, P.. On the principal eigenvalue of a periodic-parabolic operator. Comm. Partial Differential Equations 9 (1984), 919–941.CrossRefGoogle Scholar
5Berestycki, H. and Lions, P. L.. Some Applications of the Method of Super and Subsolutions. Springer Lecture Notes in Mathematics 782, pp. 16–41 (Berlin: Springer-Verlag, 1980).Google Scholar
6Brown, K. J. and Lin, C. C.. On the existence of positive eigenfunctions for an eigenvalue problem with indefinite weight-function. J. Math. Anal. Appl. 75 (1980), 112–120.CrossRefGoogle Scholar
7Cantrell, R. S. and Cosner, C.. On the positone problem for elliptic systems. Indiana Univ. Math. J. 34 (1985), 517–532.CrossRefGoogle Scholar
8Cantrell, R. S. and Cosner, C.. On the steady-state problem for the Volterra-Lotka competition model with diffusion. Houston J. Math 13 (1987), 337–352.Google Scholar
9Cantrell, R. S. and Schmitt, K.. On the eigenvalue problem for coupled elliptic systems. SIAM J. Math. Anal. 17 (1986), 850–862.CrossRefGoogle Scholar
10Cosner, C. and Lazer, A. C.. Stable coexistence states in the Volterra-Lotka competitionmodel with diffusion. SIAM J. Appl. Math. 44 (1984), 1112–1132.CrossRefGoogle Scholar
11Cosner, C. and Schindler, F.. Upper and lower solutions for systems of second order equations with nonnegative characteristic form and discontinuous coefficients. Rocky Mountain J. Math. 14 (1984), 549–557.CrossRefGoogle Scholar
12Crandall, M. and Rabinowitz, P. H.. Bifurcation from simple eigenvalues. J. Funct. Anal. 8 (1971), 321–340.CrossRefGoogle Scholar
13deFigueiredo, D. G.. Positive Solutions of Semilinear Elliptic Problems. Springer Lecture Notes in Mathematics 957, pp. 34–88 (Berlin, Springer-Verlag, 1982).Google Scholar
14DeSanti, A. J.. Boundary and interior layer behavior of solutions of some singularly perturbed semilinear elliptic boundary value problems. J. Math. Pures Appl. 65 (1986), 227–262.Google Scholar
15Fife, P.. Mathematical Aspects of Reacting and Diffusing Systems. Lecture Notes in Biomathematics 28 (Berlin: Springer-Verlag, 1979).CrossRefGoogle Scholar
16Fleckinger, J. and Lapidus, M. L.. Eigenvalues of elliptic boundary value problems with an indefinite weight function. Trans. Amer. Math. Soc. 295 (1986), 305–324.CrossRefGoogle Scholar
17Fleckinger, J. and Mingarelli, A. B.. On the eigenvalues of non-definite elliptic operators. In Differential Equations, ed. Knowles, I. W. & Lewis, R. T., pp. 219–227. (Amsterdam: Elsevier, 1984).Google Scholar
18Fleming, W. H.. A selection-migration model in population genetics. J. Math. Biol. 2 (1975), 219–233.CrossRefGoogle Scholar
19Frankel, O. H. and Soulé, M. E.. Conservation and Evolution (Cambridge: Cambridge University Press, 1981).Google Scholar
20Gilbarg, D. and Trudinger, N. S.. Elliptic Partial Differential Equations of Second Order (Berlin: Springer-Verlag, 1977).CrossRefGoogle Scholar
21Gossez, J. P. and LamiDozo, E.. On the principal eigenvalue of second order elliptic problem. Arch. Rational Mech. Anal. 89 (1985), 169–175.CrossRefGoogle Scholar
22Hallam, T. G.. Population dynamics in a homogeneous environment. In Mathematical Ecology, eds Hallam, T. G. and Levin, S.. Biomathematics 17 (Berlin: Springer-Verlag, 1986).CrossRefGoogle Scholar
23Hallam, T. G. and Clark, C. E.. Nonautonomous logistic equations as models of populations in a deteriorating environment. J. Theoret. Biol. 93 (1981), 303–311.CrossRefGoogle Scholar
24Hallam, T. G., Clark, C. E. and Lassiter, R. R.. Effects of toxicants on populations: a qualitative approach I. Equilibrium environmental exposure. Ecological Modelling 18(1983), 291–304.CrossRefGoogle Scholar
25Hallam, T. G., Clark, C. E. and Jordan, S., Effects of toxicants on populations: a qualitative approach II. First order kinetics. J. Math. Biol. 18 (1983), 25–37.CrossRefGoogle ScholarPubMed
26Hallam, T. G. and Luna, J. T. de. Effects of toxicants on populations: a qualitative approach III. Environmental and food chain pathways. J. Theoret. Biol. 109 (1984), 411–429.CrossRefGoogle Scholar
27Hallam, T. G. and Zhien, Ma. On density and extinction in continuous population models. J. Math. Biol. 25 (1987), 191–201.CrossRefGoogle ScholarPubMed
28Hallam, T. G. and Zhien, Ma. Persistence in population models with demographic fluctuations. J. Math. Biol. 24 (1986), 327–339.CrossRefGoogle ScholarPubMed
29Henry, D.. Geometric Theory of Semilinear Parabolic Equations. Lecture Notes in Mathematics 840 (Berlin: Springer-Verlag, 1981).CrossRefGoogle Scholar
30Hess, P.. On the eigenvalue problem for weakly coupled elliptic systems. Arch. Rational Mech. Anal. 81 (1983), 151–159.CrossRefGoogle Scholar
31Hess, P.. On bifurcation and stability of positive solutions of nonlinear elliptic eigenvalue problems. In Dynamical Systems II., ed. Bednarek, A. R. & Cesari, L., pp. 103–119 (New York: Academic Press, 1982).Google Scholar
32Hess, P. and Kato, T.. On some linear and nonlinear eigenvalue problems with an indefinite weight function. Comm. Partial Differential Equations 5 (1980), 999–1030.CrossRefGoogle Scholar
33Lazer, A. C.. Personal communication.Google Scholar
34Levin, S.. Population models and community structure in heterogeneous environments. In Mathematical Ecology, eds Hallam, T. G. and Levin, S.. Biomathematics 17 (Berlin: SpringerVerlag, 1986).Google Scholar
35MacArthur, R. H. and Wilson, E. O.. The Theory of Island Biogeography. (Princeton: Princeton University Press, 1967).Google Scholar
36Manes, A. and Micheletti, A.-M.. Un'estensione della teoria variazionale classicadegli antovaloriper operatori ellittici del secondo ordine. Boll. Un. Mat. Ital. 7(1973), 285–301.Google Scholar
37Mingarelli, A. B.. Personal communication.Google Scholar
38Newmark, W. D.. Species-area relationship and its determinants for mammals in western North American national parks. Biol. J. Linnean Soc. 28 (1986), 83–98.CrossRefGoogle Scholar
39Nussbaum, R. D.. Positive operators and elliptic eigenvalue problems. Math. Z. 186 (1984), 247–264.CrossRefGoogle Scholar
40Rabinowitz, P. H.. Some global results for nonlinear eigenvalue problems. J. Fund. Anal. 7 (1971), 487–513.CrossRefGoogle Scholar
41Rudin, W.. Real and Complex Analysis (New York: McGraw-Hill, 1987).Google Scholar
42Saut, J. C. and Scheurer, B.. Remarks on a non-linear equation arising in population genetics. Comm. Partial Differential Equations 3 (1978), 907–931.CrossRefGoogle Scholar
43Smoller, J.. Shock Waves and Reaction-Diffusion Equations (Berlin: Springer-Verlag, 1983).CrossRefGoogle Scholar
44Verhulst, P. E.. Notice sur la loi que la population suit dans sou accroissment. Correspondences Math. Phys. 10 (1838), 113–121.Google Scholar
45Verhulst, P. F.. Deuxieme me'moire sur la loi d'accroissement de la population. Mem. Acad. Roy. Belg. 20 (1847), 1–32.Google Scholar
46Weinberger, H. F.. Personal communication.Google Scholar