Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-18T23:20:26.726Z Has data issue: false hasContentIssue false
  • English
  • Français

On the free time minimizers of the Newtonian N-body problem

Published online by Cambridge University Press:  26 November 2013

ADRIANA DA LUZ  and
EZEQUIEL MADERNA
ADRIANA DA LUZ
Affiliation:
Centro de Matemática, Universidad de la Repüblica, Iguá 4225, CP 11400 Montevideo, Uruguay. e-mail: emaderna@cmat.edu.uy
EZEQUIEL MADERNA
Affiliation:
Centro de Matemática, Universidad de la Repüblica, Iguá 4225, CP 11400 Montevideo, Uruguay. e-mail: emaderna@cmat.edu.uy
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the existence and the dynamics of a very special class of motions, which satisfy a strong global minimization property. More precisely, we call a free time minimizer a curve which satisfies the least action principle between any pair of its points without the constraint of time for the variations. An example of a free time minimizer defined on an unbounded interval is a parabolic homothetic motion by a minimal central configuration. The existence of a large amount of free time minimizers can be deduced from the weak KAM theorem. In particular, for any choice of x0, there should be at least one free time minimizer x(t) defined for all t ≥ 0 and satisfying x(0)=x0. We prove that such motions are completely parabolic. Using Marchal's theorem we deduce as a corollary that there are no entire free time minimizers, i.e. defined on 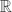$\mathbb{R}$. This means that the Mañé set of the Newtonian N-body problem is empty.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 156 , Issue 2 , March 2014 , pp. 209 - 227
Copyright
Copyright © Cambridge Philosophical Society 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abbondandolo, A. and Schwarz, M.A smooth pseudo-gradient for the Lagrangian action functional. Adv. Nonlinear Stud. 9 (2009), no. 4, 597–623.CrossRefGoogle Scholar
[2]Barutello, V., Terracini, S. and Verzini, G. Entire parabolic trajectories as minimial phase transitions. Calc. Var. Partial Differential Equations, to appear (2011).CrossRefGoogle Scholar
[3]Barutello, V., Terracini, S. and Verzini, G. Entire parabolic trajectories: the planar anisotropic Kepler problem. phArch. Ration. Mech. Anal., to appear (2011).CrossRefGoogle Scholar
[4]Chenciner, A.Action minimizing solutions of the Newtonian n-body problem: from homology to symmetry. Proceedings of the International Congress of Mathematicians, Vol. III (Beijing, 2002), 279–294 (Higher Ed. Press, Beijing, 2002).Google Scholar
[5]Chenciner, A.Collisions totales, mouvements complètement paraboliques et réduction des homothéties dans le problème des n corps. (French) J. Moser at 70 (Russian). Regul. Chaotic Dyn. 3 (1998), no. 3, 93–106.CrossRefGoogle Scholar
[6]Contreras, G.Action potential and weak KAM solutions. Calc. Var. Partial Differential Equations 13 (2001), no. 4, 427–458.CrossRefGoogle Scholar
[7]Contreras, G. and Paternain, G. P.Connecting orbits between static classes for generic Lagrangian systems. Topology 41 (2002), no. 4, 645–666.CrossRefGoogle Scholar
[8]Fathi, A. and Maderna, E.Weak KAM theorem on non compact manifolds. NoDEA Nonlinear Differential Equations Appl. 14 (2007), no. 1–2, 1–27.CrossRefGoogle Scholar
[9]Ferrario, D. and Terracini, S.On the existence of collisionless equivariant minimizers for the classical n-body problem. Invent. Math. 155 (2004), no. 2, 305–362.CrossRefGoogle Scholar
[10]Maderna, E.On weak KAM theory for N-body problems. Ergodic Theory Dynam. Systems 32 (2012) no. 3, 1019–1041.Google Scholar
[11]Maderna, E.Translation invariance of weak KAM solutions of the Newtonian N-body problem. (2011) phProc. Amer. Math. Soc. 141 (2013), 2809–2816.CrossRefGoogle Scholar
[12]Maderna, E. and Venturelli, A.Globally minimizing parabolic motions in the Newtonian N-body Problem. Arch. Ration. Mech. Anal. 194 (2009), no. 1, 283–313.CrossRefGoogle Scholar
[13]Mañé, R.Lagrangian flows: the dynamics of globally minimizing orbits. Bol. Soc. Brasil. Mat. (N.S.) 28 (1997), no. 2, 141–153.CrossRefGoogle Scholar
[14]Marchal, C.How the method of minimization of action avoids singularities. Celestial Mech. Dynam. Astronom. 83 (2002), no. 1–4, 325–353.CrossRefGoogle Scholar
[15]Marchal, C. and Saari, D.On the final evolution of the n-body problem. J. Differential Equations 20 (1976), no. 1, 150–186.CrossRefGoogle Scholar
[16]Mather, J.Action minimizing invariant measures for positive definite Lagrangian systems. Math. Z. 207 (1991) no. 2, 169–207.CrossRefGoogle Scholar
[17]Pollard, H.The behavior of gravitational systems. J. Math. Mech. 17 (1967), 601–611.Google Scholar
[18]Saari, D.Expanding gravitational systems. Trans. Amer. Math. Soc. 156 (1971), 219–240.CrossRefGoogle Scholar
[19]Wintner, A.The analytical foundations of Celestial Mechanics. Princeton Mathematical Series, Vol. 5 (Princeton University Press, Princeton, N. J., 1941).Google Scholar