Article contents
Random walk and electric currents in networks
Published online by Cambridge University Press: 24 October 2008
Abstract
Let G be a locally finite connected graph and c be a positive real-valued function defined on its edges. Let D(ξ) denote the sum of the values of c on the edges incident with a vertex ξ. A particle starts at some vertex α and performs an infinite random walk
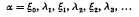
in which (i) the ξj are vertices of G, (ii), λj. is an edge joining ξj–1 to ξj (j = 1, 2, 3, …), (iii) if λ is any edge incident with ξj, then
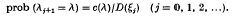
Let υ be a set of vertices of G such that the complementary set of vertices is finite and includes α. A geometrical characterization is given of the probability (τ, say) that the particle will visit some element of υ without first returning to α. An essentially equivalent problem is obtained by regarding G as an electrical network and c(λ) as the conductance of an edge λ; the current flowing through the network from α to υ when an external agency maintains α at potential I and all elements of υ at potential 0 is found to be τD(α).
A necessary and sufficient condition (of a geometrical character) for the particle to be certain to return to α. is obtained; and, as an application, a new proof is given of a conjecture of Gillis (3) regarding centrally biased random walk on an n–dimensional lattice.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 55 , Issue 2 , April 1959 , pp. 181 - 194
- Copyright
- Copyright © Cambridge Philosophical Society 1959
References
REFERENCES
- 136
- Cited by




