Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-25T05:40:55.829Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling laws and flow structures of double diffusive convection in the finger regime

Published online by Cambridge University Press:  08 August 2016

Yantao Yang Open the ORCID record for Yantao Yang [Opens in a new window] ,
Roberto Verzicco  and
Detlef Lohse
Yantao Yang*
Affiliation:
Physics of Fluids Group, MESA$+$ Research Institute, and J. M. Burgers Centre for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Roberto Verzicco
Affiliation:
Physics of Fluids Group, MESA$+$ Research Institute, and J. M. Burgers Centre for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands Dipartimento di Ingegneria Industriale, University of Rome ‘Tor Vergata’, Via del Politecnico 1, Roma 00133, Italy
Detlef Lohse
Affiliation:
Physics of Fluids Group, MESA$+$ Research Institute, and J. M. Burgers Centre for Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands Max-Planck Institute for Dynamics and Self-Organization, 37077 Göttingen, Germany
*
†Email address for correspondence: yantao.yang@utwente.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations are conducted for double diffusive convection (DDC) bounded by two parallel plates. The Prandtl numbers, i.e. the ratios between the viscosity and the molecular diffusivities of scalars, are similar to the values of seawater. The DDC flow is driven by an unstable salinity difference (here across the two plates) and stabilized at the same time by a temperature difference. For these conditions the flow can be in the finger regime. We develop scaling laws for three key response parameters of the system: the non-dimensional salinity flux 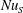$\mathit{Nu}_{S}$ mainly depends on the salinity Rayleigh number 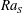$\mathit{Ra}_{S}$, which measures the strength of the salinity difference and exhibits a very weak dependence on the density ratio $\unicode[STIX]{x1D6EC}$, which is the ratio of the buoyancy forces induced by two scalar differences. The non-dimensional flow velocity 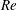$Re$ and the non-dimensional heat flux 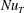$\mathit{Nu}_{T}$ are dependent on both 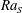$\mathit{Ra}_{S}$ and 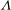$\unicode[STIX]{x1D6EC}$. However, the rescaled Reynolds number $Re\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D6FC}_{u}^{eff}}$ and the rescaled convective heat flux 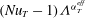$(\mathit{Nu}_{T}-1)\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D6FC}_{T}^{eff}}$ depend only on 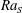$\mathit{Ra}_{S}$. The two exponents are dependent on the fluid properties and are determined from the numerical results as $\unicode[STIX]{x1D6FC}_{u}^{eff}=0.25\pm 0.02$ and $\unicode[STIX]{x1D6FC}_{T}^{eff}=0.75\pm 0.03$. 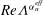Moreover, the behaviours of $\mathit{Nu}_{S}$ and $Re\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D6FC}_{u}^{eff}}$ agree with the predictions of the Grossmann–Lohse theory which was originally developed for the Rayleigh–Bénard flow. The non-dimensional salt-finger width and the thickness of the velocity boundary layers, after being rescaled by 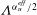$\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D6FC}_{u}^{eff}/2}$, collapse and obey a similar power-law scaling relation with 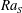$\mathit{Ra}_{S}$. When 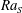$\mathit{Ra}_{S}$ is large enough, salt fingers do not extend from one plate to the other and horizontal zonal flows emerge in the bulk region. We then show that the current scaling strategy can be successfully applied to the experimental results of a heat–copper–ion system (Hage & Tilgner, Phys. Fluids, vol. 22, 2010, 076603). The fluid has different properties and the exponent 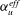$\unicode[STIX]{x1D6FC}_{u}^{eff}$ takes a different value 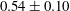$0.54\pm 0.10$.

JFM classification

Convection: Convection Convection: Double diffusive convection Geophysical and Geological Flows: Geophysical and Geological Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , pp. 667 - 689
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86 (15), 3316–3319.Google Scholar
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66 (1), 016305.Google Scholar
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16 (12), 4462–4472.Google Scholar
Hage, E. & Tilgner, A. 2010 High Rayleigh number convection with double diffusive fingers. Phys. Fluids 22 (7), 076603.Google Scholar
Holyer, J. Y. 1981 On the collective instability of salt fingers. J. Fluid Mech. 110, 195–207.Google Scholar
Kellner, M. & Tilgner, A. 2014 Transition to finger convection in double-diffusive convection. Phys. Fluids 26 (9), 094103.Google Scholar
Krishnamurti, R. 2003 Double-diffusive transport in laboratory thermohaline staircases. J. Fluid Mech. 483, 287–314.Google Scholar
Krishnamurti, R. 2009 Heat, salt and momentum transport in a laboratory thermohaline staircase. J. Fluid Mech. 638, 491–506.Google Scholar
Kunze, E. 2003 A review of oceanic salt-fingering theory. Prog. Oceanogr. 56, 399–417.Google Scholar
Linden, P. F. 1978 The formation of banded salt finger structure. J. Geophys. Res. Oceans 83 (C6), 2902–2912.Google Scholar
McDougall, T. J. & Taylor, J. R. 1984 Flux measurements across a finger interface at low values of the stability ratio. J. Mar. Res. 42, 1–14.Google Scholar
Ostilla-Mónico, R., Yang, Y., van der Poel, E. P., Lohse, D. & Verzicco, R. 2015 A multiple resolutions strategy for direct numerical simulation of scalar turbulence. J. Comput. Phys. 301, 308–321.Google Scholar
Radko, T. 2013 Double-Diffusive Convection. Cambridge University Press.Google Scholar
Radko, T., Flanagan, J. D., Stellmach, S. & Timmermans, M.-L. 2014 Double-diffusive recipes. Part II. Layer-merging events. J. Phys. Oceanogr. 44, 1285–1305.Google Scholar
Radko, T. & Smith, D. P. 2012 Equilibrium transport in double-diffusive convection. J. Fluid Mech. 692, 5–27.Google Scholar
Schmitt, R. W. 1979 Flux measurements on salt fingers at an interface. J. Mar. Res. 37, 419–436.Google Scholar
Schmitt, R. W. 1994 Double diffusion in oceanography. Annu. Rev. Fluid Mech. 26 (1), 255–285.Google Scholar
Schmitt, R. W. 2011 Thermohaline convection at density ratios below one: a new regime for salt fingers. J. Mar. Res. 69 (4–6), 779–795.Google Scholar
Schmitt, R. W., Ledwell, J. R., Montgomery, E. T., Polzin, K. L. & Toole, J. M. 2005 Enhanced diapycnal mixing by salt fingers in the thermocline of the tropical atlantic. Science 308 (5722), 685–688.Google Scholar
Shen, C. Y. 1993 Heatsalt finger fluxes across a density interface. Phys. Fluids A 5, 2633–2643.Google Scholar
Stellmach, S., Traxler, A., Garaud, P., Brummell, N. & Radko, T. 2011 Dynamics of fingering convection. Part 2. The formation of thermohaline staircases. J. Fluid Mech. 677, 554–571.Google Scholar
Stern, M. E. 1969 Collective instability of salt fingers. J. Fluid Mech. 35, 209–218.CrossRefGoogle Scholar
Stern, M. E., Radko, T. & Simeonov, J. 2001 Salt fingers in an unbounded thermocline. J. Mar. Res. 59, 355–390.Google Scholar
Stern, M. E. 1960 The salt-fountain and thermohaline convection. Tellus 12 (2), 172–175.Google Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.Google Scholar
Tait, R. I. & Howe, M. R. 1971 Thermohaline staircase. Nature 231, 178–179.Google Scholar
Taylor, J. & Bucens, P. 1989 Laboratory experiments on the structure of salt fingers. Deep Sea Res. 36 (11), 1675–1704.Google Scholar
Traxler, A., Stellmach, S., Garaud, P., Radko, T. & Brummell, N. 2011 Dynamics of fingering convection. Part 1. Small-scale fluxes and large-scale instabilities. J. Fluid Mech. 677, 530–553.Google Scholar
Turner, J. S. 1967 Salt fingers across a density interface. Deep Sea Res. 14, 599–611.Google Scholar
Yang, Y., van der Poel, E. P., Ostilla-Mónico, R., Sun, C., Verzicco, R., Grossmann, S. & Lohse, D. 2015 Salinity transfer in bounded double diffusive convection. J. Fluid Mech. 768, 476–491.Google Scholar
Yang, Y., Verzicco, R. & Lohse, D. 2016a From convection rolls to finger convection in double-diffusive turbulence. Proc. Natl Acad. Sci. USA 113 (1), 69–73.Google Scholar
Yang, Y., Verzicco, R. & Lohse, D.2016b Vertically bounded double diffusive convection in the fingering regime: comparing no-slip versus free-slip boundary conditions. Phys. Rev. Lett. (submitted) arXiv:1602.07718.Google Scholar