Hostname: page-component-76fb5796d-2lccl Total loading time: 0 Render date: 2024-04-25T07:43:41.690Z Has data issue: false hasContentIssue false
  • English
  • Français

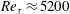Direct numerical simulation of turbulent channel flow up to $\mathit{Re}_{{\it\tau}}\approx 5200$

Published online by Cambridge University Press:  10 June 2015

Myoungkyu Lee  and
Robert D. Moser
Myoungkyu Lee
Affiliation:
Department of Mechanical Engineering, The University of Texas at Austin, TX 78712, USA
Robert D. Moser*
Affiliation:
Department of Mechanical Engineering, The University of Texas at Austin, TX 78712, USA Center for Predictive Engineering and Computational Sciences, Institute for Computational Engineering and Sciences, The University of Texas at Austin, TX 78712, USA
*
†Email address for correspondence: rmoser@ices.utexas.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

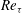A direct numerical simulation of incompressible channel flow at a friction Reynolds number ($\mathit{Re}_{{\it\tau}}$) of 5186 has been performed, and the flow exhibits a number of the characteristics of high-Reynolds-number wall-bounded turbulent flows. For example, a region where the mean velocity has a logarithmic variation is observed, with von Kármán constant 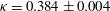${\it\kappa}=0.384\pm 0.004$. There is also a logarithmic dependence of the variance of the spanwise velocity component, though not the streamwise component. A distinct separation of scales exists between the large outer-layer structures and small inner-layer structures. At intermediate distances from the wall, the one-dimensional spectrum of the streamwise velocity fluctuation in both the streamwise and spanwise directions exhibits 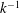$k^{-1}$ dependence over a short range in wavenumber 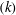$(k)$. Further, consistent with previous experimental observations, when these spectra are multiplied by 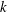$k$ (premultiplied spectra), they have a bimodal structure with local peaks located at wavenumbers on either side of the 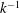$k^{-1}$ range.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 774 , 10 July 2015 , pp. 395 - 415
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afzal, N. 1976 Millikan’s argument at moderately large Reynolds number. Phys. Fluids 19 (4), 600–602.CrossRefGoogle Scholar
Afzal, N. 1982 Fully developed turbulent flow in a pipe: an intermediate layer. Ing.-Arch. 52, 355–377.CrossRefGoogle Scholar
Afzal, N. & Yajnik, K. 1973 Analysis of turbulent pipe and channel flows at moderately large Reynolds number. J. Fluid Mech. 61, 23–31.CrossRefGoogle Scholar
Bailey, S. C. C., Vallikivi, M., Hultmark, M. & Smits, A. J. 2014 Estimating the value of von Kármán’s constant in turbulent pipe flow. J. Fluid Mech. 749, 79–98.CrossRefGoogle Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to $Re_{{\it\tau}}$ = 4000. J. Fluid Mech. 742, 171–191.CrossRefGoogle Scholar
Borrell, G., Sillero, J. A. & Jiménez, J. 2013 A code for direct numerical simulation of turbulent boundary layers at high Reynolds numbers in BG/P supercomputers. Comput. Fluids 80, 37–43.CrossRefGoogle Scholar
Botella, O. & Shariff, K. 2003 B-spline methods in fluid dynamics. Intl J. Comput. Fluid Dyn. 17 (2), 133–149.CrossRefGoogle Scholar
Buschmann, M. H. & Gad-el-Hak, M. 2003 Generalized logarithmic law and its consequences. AIAA J. 41 (1), 40–48.CrossRefGoogle Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.CrossRefGoogle Scholar
Comte-Bellot, G.1963 Contribution à l’étude de la turbulence de conduite. PhD thesis, University of Grenoble, France.Google Scholar
Dean, R. B. & Bradshaw, P. 1976 Measurements of interacting turbulent shear layers in a duct. J. Fluid Mech. 78, 641–676.Google Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
Del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Dixit, S. A. & Ramesh, O. N. 2013 On the $k_{1}^{-1}$ scaling in sink-flow turbulent boundary layers. J. Fluid Mech. 737, 329–348.Google Scholar
Durbin, P. A. & Pettersson Reif, B. A. 2010 Statistical Theory and Modeling for Turbulent Flows. Wiley.CrossRefGoogle Scholar
El Khoury, G. K., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91 (3), 475–495.Google Scholar
Fernholz, H. H. & Finley, P. J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci. 32 (8), 245–311.CrossRefGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Hinze, J. O. 1975 Turbulence. McGraw-Hill.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $Re_{{\it\tau}}=2003$ . Phys. Fluids 18 (1), 011702.Google Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20 (10), 101511.Google Scholar
Hultmark, M., Bailey, S. C. C. & Smits, A. J. 2010 Scaling of near-wall turbulence in pipe flow. J. Fluid Mech. 649, 103–113.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108, 094501.CrossRefGoogle ScholarPubMed
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.CrossRefGoogle Scholar
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145 (2), 273–306.Google Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google ScholarPubMed
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Jiménez, J. & Moser, R. D. 2007 What are we learning from simulating wall turbulence? Phil. Trans. R. Soc. Lond. A 365 (1852), 715–732.Google ScholarPubMed
Johansson, A. V. & Alfredsson, P. H. 1982 On the structure of turbulent channel flow. J. Fluid Mech. 122, 295–314.CrossRefGoogle Scholar
Johnson, R. W. 2005 Higher order B-spline collocation at the Greville abscissae. Appl. Numer. Maths 52 (1), 63–75.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417.CrossRefGoogle Scholar
Kulandaivelu, V.2011 Evolution and structure of zero pressure gradient turbulent boundary layer. PhD thesis, University of Melbourne.Google Scholar
Kunkel, G. J. & Marusic, I. 2006 Study of the near-wall-turbulent region of the high-Reynolds-number boundary layer using an atmospheric flow. J. Fluid Mech. 548, 375–402.CrossRefGoogle Scholar
Kwok, W. Y., Moser, R. D. & Jiménez, J. 2001 A critical evaluation of the resolution properties of B-spline and compact finite difference methods. J. Comput. Phys. 174 (2), 510–551.CrossRefGoogle Scholar
Lee, M., Malaya, N. & Moser, R. D. 2013 Petascale direct numerical simulation of turbulent channel flow on up to 786K cores. In Proceedings of SC13: International Conference for High Performance Computing, Networking, Storage and Analysis. ACM.Google Scholar
Lee, M., Ulerich, R., Malaya, N. & Moser, R. D. 2014 Experiences from leadership computing in simulations of turbulent fluid flows. Comput. Sci. Engng 16 (5), 24–31.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to $Re_{{\it\tau}}$ = 4200. Phys. Fluids 26 (1), 011702.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010a High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31 (3), 418–428.CrossRefGoogle Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010b Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Millikan, C. B. 1938 A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of the 5th International Congress for Applied Mechanics, pp. 386–392. Wiley.Google Scholar
Mizuno, Y. & Jiménez, J. 2011 Mean velocity and length-scales in the overlap region of wall-bounded turbulent flows. Phys. Fluids 23 (8), 085112.CrossRefGoogle Scholar
Moin, P. 2009 Revisiting Taylor’s hypothesis. J. Fluid Mech. 640, 1–4.Google Scholar
Monty, J. P.2005 Developments in smooth wall turbulent duct flows. PhD thesis, University of Melbourne.Google Scholar
Monty, J. P. & Chong, M. S. 2009 Turbulent channel flow: comparison of streamwise velocity data from experiments and direct numerical simulation. J. Fluid Mech. 633, 461–474.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.CrossRefGoogle Scholar
Morrison, J. F., McKeon, B. J., Jiang, W. & Smits, A. J. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.CrossRefGoogle Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to $Re_{{\it\tau}}=590$ . Phys. Fluids 11 (4), 943–945.Google Scholar
Nagib, H., Christophorou, C., Reudi, J.-D., Monkewitz, P., Österlun, J. & Gravante, S.2004 Can we ever rely on results from wall-bounded turbulent flows without direct measurements of wall shear stress. In 24th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Portland, Oregon, p. 2392. American Institute of Aeronautics and Astronautics (AIAA).CrossRefGoogle Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20 (10), 101518.Google Scholar
Nickels, T., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the $k_{1}^{-1}$ law in a high-Reynolds-number turbulent boundary layer. Phys. Rev. Lett. 95 (7), 074501.CrossRefGoogle Scholar
Nickels, T. B., Marusic, I., Hafez, S., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. Lond. A 365 (1852), 807–822.Google ScholarPubMed
Oliver, T. A., Malaya, N., Ulerich, R. & Moser, R. D. 2014 Estimating uncertainties in statistics computed from direct numerical simulation. Phys. Fluids 26 (3), 035101.CrossRefGoogle Scholar
Österlund, J. M., Johansson, A. V., Nagib, H. M. & Hites, M. H. 2000 A note on the overlap region in turbulent boundary layers. Phys. Fluids 12 (1), 1–4.Google Scholar
Panton, R. L. 2007 Composite asymptotic expansions and scaling wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 733–754.Google ScholarPubMed
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Rosenberg, B. J., Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers. J. Fluid Mech. 731, 46–63.CrossRefGoogle Scholar
Schultz, M. P. & Flack, K. A. 2013 Reynolds-number scaling of turbulent channel flow. Phys. Fluids 25 (2), 025104.CrossRefGoogle Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to ${\it\delta}^{+}\approx 2000$ . Phys. Fluids 25, 105102.CrossRefGoogle Scholar
Smits, A. J. & Marusic, I. 2013 Wall-bounded turbulence. Phys. Today 66 (9), 25–30.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43 (1), 353–375.CrossRefGoogle Scholar
Spalart, P. R. & Allmaras, S. R. 1992 A one-equation turbulence model for aerodynamic flows. In 30th Aerospace Sciences Meeting and Exhibit, p. 439. American Institute of Aeronautics and Astronautics.Google Scholar
Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and two periodic directions. J. Comput. Phys. 96 (2), 297–324.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Vreman, A. W. & Kuerten, J. G. M. 2014 Comparison of direct numerical simulation databases of turbulent channel flow at $Re_{{\it\tau}}=180$ . Phys. Fluids 26 (1), 015102.CrossRefGoogle Scholar
Wei, T. & Willmarth, W. W. 1989 Reynolds-number effects on the structure of a turbulent channel flow. J. Fluid Mech. 204, 57–95.Google Scholar
Westerweel, J., Elsinga, G. E. & Adrian, R. J. 2013 Particle image velocimetry for complex and turbulent flows. Annu. Rev. Fluid Mech. 45 (1), 409–436.Google Scholar
Winkel, E. S., Cutbirth, J. M., Ceccio, S. L., Perlin, M. & Dowling, D. R. 2012 Turbulence profiles from a smooth flat-plate turbulent boundary layer at high Reynolds number. Exp. Therm. Fluid Sci. 40, 140–149.CrossRefGoogle Scholar
Wosnik, M., Castillo, L. & George, W. K. 2000 A theory for turbulent pipe and channel flows. J. Fluid Mech. 421, 115–145.CrossRefGoogle Scholar
Wu, X., Baltzer, J. R. & Adrian, R. J. 2012 Direct numerical simulation of a 30R long turbulent pipe flow at $R^{+}=685$ : large- and very large-scale motions. J. Fluid Mech. 698, 235–281.CrossRefGoogle Scholar
Zanoun, E.-S., Durst, F. & Nagib, H. 2003 Evaluating the law of the wall in two-dimensional fully developed turbulent channel flows. Phys. Fluids 15 (10), 3079.CrossRefGoogle Scholar
Zanoun, E.-S., Nagib, H. & Durst, F. 2009 Refined $c_{f}$ relation for turbulent channels and consequences for high- $Re$ experiments. Fluid Dyn. Res. 41 (2), 021405.CrossRefGoogle Scholar