Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-18T22:54:52.275Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON SIMULTANEOUS AND MULTIPLICATIVE DIOPHANTINE APPROXIMATION ON PLANAR CURVES

Published online by Cambridge University Press:  09 August 2007

DZMITRY BADZIAHIN  and
JASON LEVESLEY
DZMITRY BADZIAHIN
Affiliation:
Department of Mathematics, University of York, Heslington, York, YO10 5DD, United Kingdom e-mails: db528@york.ac.uk, jl107@york.ac.uk
JASON LEVESLEY
Affiliation:
Department of Mathematics, University of York, Heslington, York, YO10 5DD, United Kingdom e-mails: db528@york.ac.uk, jl107@york.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

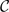Let be a non-degenerate planar curve. We show that the curve is of Khintchine-type for convergence in the case of simultaneous approximation in 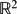with two independent approximation functions; that is if a certain sum converges then the set of all points (x,y) on the curve which satisfy simultaneously the inequalities ||qx|| < ψ1(q) and ||qy|| < ψ2(q) infinitely often has induced measure 0. This completes the metric theory for the Lebesgue case. Further, for multiplicative approximation ||qx|| ||qy|| < ψ(q) we establish a Hausdorff measure convergence result for the same class of curves, the first such result for a general class of manifolds in this particular setup.

Keywords

Primary 11J83Secondary 11J1311K60
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 49 , Issue 2 , May 2007 , pp. 367 - 375
Copyright
Copyright © Glasgow Mathematical Journal Trust 2007

References

REFERENCES

1. Beresnevich, V., Dickinson, D. and Velani, S., Measure theoretic laws for lim sup sets, Mem. Amer. Math. Soc. 179 (2006), no. 846.Google Scholar
2. Beresnevich, V., Dickinson, H. and Velani, S.. Diophantine approximation on planar curves and the distribution of rational points, with an Appendix, Sums of two squares near perfect squares, by Vaughan, R. C., Ann Math., to appear: Preprint (53pp) arXiv:math.NT/0401148.Google Scholar
3. Beresnevich, V. and Velani, S., A note on simultaneous Diophantine approximation on planar curves. Preprint (23pp) arXiv:math.NT/0412141.Google Scholar
4. Falconer, K., Fractal geometry: mathematical foundations and applications (Wiley, 1990).Google Scholar
5. Falconer, K., Techniques in fractal geometry (Wiley, 1997).Google Scholar
6. Mattila, P., Geometry of sets and measures in Euclidean space, Cambridge Studies in Advanced Mathematics, No. 44, (Cambridge University Press, 1995).CrossRefGoogle Scholar
7. Vaughan, R. C. and Velani, S., Diophantine approximation on planar curves: the convergence theory, Invent. Math 166 (2006), 103–124.Google Scholar