Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-24T04:56:16.311Z Has data issue: false hasContentIssue false
  • English
  • Français

In-homogenous self-similar measures and their Fourier transforms

Published online by Cambridge University Press:  01 March 2008

L. OLSEN  and
N. SNIGIREVA
L. OLSEN
Affiliation:
Department of Mathematics, University of St. Andrews, St. Andrews, Fife KY16 9SS, Scotland. e-mail: lo@st-and.ac.uk
N. SNIGIREVA
Affiliation:
Department of Mathematics, University of St. Andrews, St. Andrews, Fife KY16 9SS, Scotland. e-mail: ns93@st-and.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Sj: ℝd → ℝd for j = 1, . . ., N be contracting similarities. Also, let (p1,. . ., pN, p) be a probability vector and let ν be a probability measure on ℝd with compact support. We show that there exists a unique probability measure μ such that 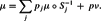The measure μ is called an in-homogenous self-similar measure. In this paper we study the asymptotic behaviour of the Fourier transforms of in-homogenous self-similar measures. Finally, we present a number of applications of our results. In particular, non-linear self-similar measures introduced and investigated by Glickenstein and Strichartz are special cases of in-homogenous self-similar measures, and as an application of our main results we obtain simple proofs of generalizations of Glickenstein and Strichartz's results on the asymptotic behaviour of the Fourier transforms of non-linear self-similar measures.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 2 , March 2008 , pp. 465 - 493
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ba1]Barnsley, M. F.Fractals Everywhere, 2nd ed. (Academic Press, 1993).Google Scholar
[Ba2]Barnsley, M. F. Existence and uniqueness of orbital measures. Preprint, http://arxiv.org/abs/ math.DS/0508010.Google Scholar
[Ba3]Barnsley, M. F.Superfractals (Cambridge University Press, 2006).CrossRefGoogle Scholar
[BD]Barnsley, M. F. and Demko, S.. Iterated function systems and the global construction of fractals. Proc. Roy. Soc. London Ser. A 399 (1985), 243–275.Google Scholar
[Bl]Bluhm, C.Fourier asymptotics of statistically self-similar measures. J. Fourier Anal. Appl. 5 (1999), 355–362.CrossRefGoogle Scholar
[Fa]Falconer, K. J.Techniques in Fractal Geometry (John Wiley & Sons Ltd., 1997).Google Scholar
[GS]Glickenstein, D. and Strichartz, R. S.. Nonlinear self-similar measures and their Fourier transforms. Indiana U. Math. J. 45 (1996), 205–220.CrossRefGoogle Scholar
[HL]Hu, T.-Y. and Lau, K.-S.. Fourier asymptotics of Cantor type measures at infinity. Proc. Amer. Math. Soc. 130 (2002), 2711–2717.CrossRefGoogle Scholar
[Hu]Hu, T.-Y.. Asymptotic behavior of Fourier transforms of self-similar measures. Proc. Amer. Math. Soc. 129 (2001), 1713–1720.CrossRefGoogle Scholar
[Hut]Hutchinson, J. E.Fractals and self-similarity. Indiana U. Math. J. 30 (1981), 713–747.CrossRefGoogle Scholar
[Lal1]Lalley, S.The packing and covering functions of some self-similar fractals. Indiana Univ. Math. J. 37 (1988), 699–710.CrossRefGoogle Scholar
[Lal2]Lalley, S. Probabilistic methods in certain counting problems of ergodic theory. Ergodic theory, symbolic dynamics, and hyperbolic spaces. Papers from the Workshop on Hyperbolic Geometry and Ergodic Theory held in Trieste (April 17–28, 1989). pp. 223–257. Edited by Bedford, T., Keane, M. and Series, C.. Oxford Science Publications (The Clarendon Press, Oxford University Press, 1991).Google Scholar
[Lal1]Lau, K.-S.. Fractal measures and mean p-variations. J. Funct. Anal. 108 (1992), 427–457.CrossRefGoogle Scholar
[Lal2]Lau, K.-S.. L p-spectrum and multifractal formalism. Fractal geometry and stochastics (Finsterbergen, 1994), 55–90, Progr. Probab. 37 (Birkhäuser, 1995).Google Scholar
[LW]Lau, K.-S. and Wang, J.. Mean quadratic variations and Fourier asymptotics of self-similar measures. Monatsh. Math. 115 (1993), 99–132.CrossRefGoogle Scholar
[OS]Olsen, L. and Snigireva, N.. Multifractal spectra of in-homogenous self-similar measures, preprint.Google Scholar
[Pe]Peruggia, M.Discrete Iterated Function Systems (A. K. Peters, 1994).CrossRefGoogle Scholar
[Sn]Snigireva, N. In-homogenous self-similar sets and measures. Doctoral Dissertation (University of St Andrews) in preparation.Google Scholar
[S1]Strichartz, R. S.Fourier asymptotics of fractal measures. J. Funct. Anal. 89 (1990), 154–187.CrossRefGoogle Scholar
[S2]Strichartz, R. S.Self-similar measures and their Fourier transforms. Indiana U. Math. J. 39 (1990), 797–817.CrossRefGoogle Scholar
[S3]Strichartz, R. S.Self-similar measures and their Fourier transforms. II. Trans. Amer. Math. Soc. 336 (1993), 335–361.CrossRefGoogle Scholar
[S4]Strichartz, R. S.Self-similar measures and their Fourier transforms, III. Indiana Univ. Math. J. 42 (1993), 367–411.CrossRefGoogle Scholar