Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-15T19:00:42.393Z Has data issue: false hasContentIssue false
  • English
  • Français

The multi-mode stretched spiral vortex in homogeneous isotropic turbulence

Published online by Cambridge University Press:  08 January 2008

KIYOSI HORIUTI  and
TAKEHARU FUJISAWA
KIYOSI HORIUTI
Affiliation:
Department of Mechano-Aerospace Engineering, I1-64, Tokyo Institute of Technology, 2-12-1 O-okayama, Meguro-ku, Tokyo 152-8552, Japankhoriuti@mes.titech.ac.jp
TAKEHARU FUJISAWA
Affiliation:
Department of Mechano-Aerospace Engineering, I1-64, Tokyo Institute of Technology, 2-12-1 O-okayama, Meguro-ku, Tokyo 152-8552, Japankhoriuti@mes.titech.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

The stretched spiral vortex is identified using direct numerical simulation (DNS) data for homogeneous isotropic turbulence and its properties are studied. Its genesis, growth and annihilation are elucidated, and its role in the generation of turbulence is shown. Aside from the two symmetric modes of configurations with regard to the vorticity alignment along two spiral sheets and the vortex tube in the core region studied in previous works, a third asymmetric mode is found. One of the two symmetric modes and the asymmetric mode are created not by a conventional rolling-up of a single vortex sheet but through the interaction among several sheets. The stagnation flow caused by the two sheets converges to form recirculating flow through its interaction with the vortex along the third sheet. This recirculating flow strains and stretches the sheets. The vortex tube is formed by axial straining, lowering of pressure and the intensification of the swirling motion in the recirculating region. As a result of the differential rotation induced by the tube and that self-induced by the sheet, the vortex sheets are entrained by the tube and form spiral turns. The transition between the three modes is examined. The initial configuration is in one of two symmetric modes, but it is transformed into another set of two modes due to the occurrence of reorientation in the vorticity direction along the stretched sheets. The symmetric mode tends to be more persistent than the asymmetric mode, among the two transformed modes. The tightening of the spiral turns of the spiral sheets produces a cascade of velocity fluctuations to smaller scales and generates a strongly intermittent dissipation field. To precisely capture the spiral turns, a grid resolution with at least 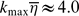(kmax is the largest wavenumber, 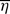is the averaged Kolmogorov scale) is required. At a higher Reynolds number, self-similar spiral vortices are successively produced by the instability cascade along the stretched vortex sheets. A cluster consisting of spiral vortices with an extensive range of length scales is formed and this cluster induces an energy cascade.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 595 , 25 January 2008 , pp. 341 - 366
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andreotti, B. 1997 Studying Burgers' models to investigate the physical meaning of the alignments statistically observed in turbulence. Phys. Fluids 9, 735–742.CrossRefGoogle Scholar
Beronov, K. N. & Kida, S. 1996 Linear two-dimensional stability of a Burgers vortex layer. Phys. Fluids 8, 1024–1035.CrossRefGoogle Scholar
Brachet, M. E., Meneguzzi, M., Vincent, A., Politano, H. & Sulem, P. L. 1992 Numerical evidence of smooth self-similar dynamics and possibility of subsequent collapse for three-dimensional ideal flows. Phys. Fluids A 4, 2845–2854.CrossRefGoogle Scholar
Burgers, J. M. 1948 A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1, 171.CrossRefGoogle Scholar
Chasnov, J. R. 1991 Simulation of the Kolmogorov inertial subrange using an improved subgrid model. Phys. Fluids A 3, 188–200.CrossRefGoogle Scholar
Childress, S. 1984 A vortex-tube model of eddies in the inertial range. Geophys. Astrophys. Fluid Dyn. 29, 29–64.CrossRefGoogle Scholar
Dávila, J. & Vassilicos, J. C. 2003 Richardson's pair diffusion and the stagnation point structure of turbulence. Phys. Rev. Lett. 91, 144501.CrossRefGoogle ScholarPubMed
Gilbert, A. D. 1993 A cascade interpretation of Lundgren's stretched spiral vortex model for turbulent fine structure. Phys. Fluids A 5, 2831–2834.CrossRefGoogle Scholar
Herring, J. R. & Kerr, R. M. 1993 Development of enstrophy and spectra in numerical turbulence. Phys. Fluids A 5, 2792–2798.CrossRefGoogle Scholar
Holm, D. D. & Kerr, R. M. 2002 Transient vortex events in the initial value problem for turbulence. Phys. Rev. Lett. 88, 244501.CrossRefGoogle ScholarPubMed
Horiuti, K. 2001 A classification method for vortex sheet and tube structures in turbulent flows. Phys. Fluids 13, 3756–3774.CrossRefGoogle Scholar
Horiuti, K. 2003 Roles of nonaligned eigenvectors of strain-rate and subgrid-scale stress tensors in turbulence generation. J. Fluid Mech. 491, 65–100.CrossRefGoogle Scholar
Horiuti, K. & Takagi, Y. 2005 Identification method for vortex sheet structures in turbulent flows. Phys. Fluids 17, 121703.CrossRefGoogle Scholar
Jiménez, J. & Wray, A. A. 1998 On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech. 373, 255–285.CrossRefGoogle Scholar
Kawahara, G. 2005 Energy dissipation in spiral vortex layers wrapped around a straight vortex tube. Phys. Fluids 17, 055111.CrossRefGoogle Scholar
Kawahara, G., Kida, S., Tanaka, M. & Yanase, S. 1997 Wrap, tilt and stretch of vorticity lines around a strong thin straight vortex tube in a simple shear flow. J. Fluid Mech. 353, 115–162.CrossRefGoogle Scholar
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–325.CrossRefGoogle Scholar
Kerr, O. S. & Dold, J. W. 1994 Periodic steady vortices in a stagnation-point flow. J. Fluid Mech. 491, 307–325.CrossRefGoogle Scholar
Kida, S. & Miura, H. 1998 Identification and analysis of vortical structures Eur. J. Mech. B Fluids 17, 471–488.CrossRefGoogle Scholar
Kida, S. & Miura, H. 2000 Double spirals around a tubular vortex in turbulence. J. Phys. Soc. Japan 69, 3466–3467.CrossRefGoogle Scholar
Lundgren, T. S. 1982 Strained spiral vortex model for turbulent structures. Phys. Fluids 25, 2193–2203.CrossRefGoogle Scholar
Lundgren, T. S. 1993 A small-scale turbulence model. Phys. Fluids A 5, 1472–1483.CrossRefGoogle Scholar
Lundgren, T. S. & Mansour, N. N. 1996 Transition to turbulence in an elliptic vortex. J. Fluid Mech. 307, 43–62.CrossRefGoogle Scholar
Malik, N. A. & Vassilicos, J. C. 1996 Eulerian and Lagrangian scaling properties of randomly advected vortex tubes. J. Fluid Mech. 326, 417–436.CrossRefGoogle Scholar
Moore, D. W. 1985 The interaction of a diffusing vortex and an aligned shear flow. Proc. R. Soc. Lond. A 399, 367–375.Google Scholar
Neu, J. C. 1984 The dynamics of stretched vortices. J. Fluid Mech. 143, 253–276.CrossRefGoogle Scholar
Nomura, K. K. & Post, G. K. 1998 The structure and dynamics of vorticity and rate of strain in incompressible homogeneous turbulence. J. Fluid Mech. 377, 65–97.CrossRefGoogle Scholar
Passot, T., Politano, H., Sulem, P.-L. & Meneguzzi, M. 1995 Instability of strained vortex layers and vortex tube formation in homogeneous turbulence. J. Fluid Mech. 282, 313–338.CrossRefGoogle Scholar
Pearson, C. F. & Abernathy, F. H. 1984 Evolution of the flow field associated with a streamwise diffusing vortex. J. Fluid Mech. 146, 271–283.CrossRefGoogle Scholar
Pullin, D. I. & Lundgren, T. S. 2001 Axial motion and scalar transport in stretched spiral vortices. Phys. Fluids 13, 2553–2563.CrossRefGoogle Scholar
Pumir, A. 1996 A numerical study of pressure fluctuations in three-dimensional, incompressible, homogeneous, isotropic turbulence. Phys. Fluids 6, 2071–2083.CrossRefGoogle Scholar
Rosales, C. & Meneveau, C. 2006 A minimal multiscale Lagrangian map approach to systhesize non-Gaussian turbulent vector fields. Phys. Fluids 18, 075104.CrossRefGoogle Scholar
Ruetsh, G. R. & Maxey, M. R. 1992 The evolution of small-scale structures in homogeneous turbulence. Phys. Fluids A 4, 2747–2760.CrossRefGoogle Scholar
Schumacher, J., Sreenivasan, K. R. & Yeung, P. K. 2005 Very fine structures in scalar mixing. J. Fluid Mech. 531, 113–122.CrossRefGoogle Scholar
Sreenivasan, K. R. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10, 528–529.CrossRefGoogle Scholar
Sreenivasan, K. R. 2004 Possible effects of small-scale intermittency in turbulent reacting flows. Flow, Turbulence Combust. 72, 115–131.CrossRefGoogle Scholar
Sulem, C., Sulem, P. L. & Frisch, H. 1983 Tracing complex singularities with spectral methods. J. Comput Phys. 50, 138–161.CrossRefGoogle Scholar
Verzicco, R., Jiménez, J. & Orlandi, P. 1995 On steady columnar vortices under local compression. J. Fluid Mech. 299, 367–388.CrossRefGoogle Scholar
Vincent, A. & Meneguzzi, M. 1994 The dynamics of vorticity tubes in homogeneous turbulence. J. Fluid Mech. 258, 245–254.CrossRefGoogle Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15, 1517–1534.CrossRefGoogle Scholar