Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-25T10:57:52.933Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillatory motion and wake of a bubble rising in a thin-gap cell

Published online by Cambridge University Press:  30 July 2015

Audrey Filella ,
Patricia Ern  and
Véronique Roig
Audrey Filella
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse); Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT; F-31400 Toulouse, France
Patricia Ern
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse); Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT; F-31400 Toulouse, France
Véronique Roig*
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse); Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT; F-31400 Toulouse, France
*
†Email address for correspondence: roig@imft.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the characteristics of the oscillatory motion and wake of confined bubbles freely rising in a thin-gap cell (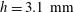$h=3.1~\text{mm}$ width). Once the diameter 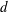$d$ of the bubble in the plane of the cell is known, the mean vertical velocity of the bubble 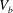$V_{b}$ is proportional to the gravitational velocity 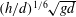$(h/d)^{1/6}\sqrt{gd}$, where 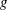$g$ is the gravitational acceleration. This velocity is used to build the Reynolds number 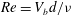$Re=V_{b}d/{\it\nu}$ that characterizes the flow induced by the bubble in the surrounding liquid (of kinematic viscosity ${\it\nu}$), and which determines at leading order the mean deformation of the bubble given by the aspect ratio 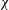${\it\chi}$ of the ellipse equivalent to the bubble contour. We then show that in the reference frame associated with the bubble (having a fixed origin and axes corresponding to the minor and major axes of the equivalent ellipse) the characteristics of its oscillatory motion in the plane of the cell display remarkable properties in the range 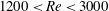$1200<Re<3000$ and 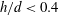$h/d<0.4$. In particular, the velocity of the bubble presents along its path an almost constant component along its minor axis (fluctuations in time of approximately 5 %), given by 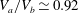$V_{a}/V_{b}\simeq 0.92$ for all 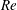$Re$. The dimensionless amplitude of oscillation of the angular velocity is also constant for all 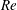$Re$, 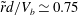$\tilde{r}d/V_{b}\simeq 0.75$, while that of the transverse velocity of the bubble (along its major axis) is given by 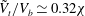$\tilde{V}_{t}/V_{b}\simeq 0.32{\it\chi}$, reaching values comparable to those of the axial velocity 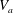$V_{a}$ for the most deformed bubbles (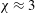${\it\chi}\approx 3$). Furthermore, the frequency 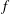$f$ of oscillation scales with the inertial time scale based on the transverse velocity of the bubble 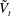$\tilde{V}_{t}$, corresponding to a constant Strouhal number 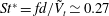$St^{\ast }=fd/\tilde{V}_{t}\simeq 0.27$. Using high-frequency particle image velocimetry, we investigate in detail the properties of the wake associated with the oscillatory motion of sufficiently confined bubbles. We observe that vortex shedding occurs for a maximal transverse velocity 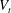$V_{t}$ of the bubble, corresponding to a maximal drift angle of the bubble. Furthermore, the measured vorticity of the vortex at detachment corresponds to the estimation 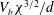$V_{b}{\it\chi}^{3/2}/d$ of the vorticity produced at the bubble surface. Three stages then emerge concerning the evolution in time of the wake generated by the bubble. For one to two periods of oscillation 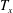$T_{x}$ following the release of a vortex, a rapid decay of the vorticity of the released vortex is observed. Meanwhile, the released vortex located initially at a distance of approximately one diameter from the bubble centre moves outwards from the bubble path and expands. At intermediate times, the vortex street undergoes vortex pairing. When viscous effects become predominant at a time of the order of the viscous time scale 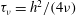${\it\tau}_{{\it\nu}}=h^{2}/(4{\it\nu})$, the vortex street becomes frozen and decays exponentially in place.

JFM classification

Drops and Bubbles: Bubble dynamics Drops and Bubbles: Drops and Bubbles
Type
Papers
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , pp. 60 - 88
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersen, A., Pesavento, U. & Wang, Z. J. 2005 Unsteady aerodynamics of fluttering and tumbling plates. J. Fluid Mech. 541, 65–90.CrossRefGoogle Scholar
Aussillous, P. & Quéré, D. 2000 Quick deposition of a fluid on the wall of a tube. Phys. Fluids 12 (10), 1070–6631.CrossRefGoogle Scholar
Bessler, W. F. & Littman, H. 1987 Experimental studies of wakes behind circularly capped bubbles. J. Fluid Mech. 185, 137–151.Google Scholar
Bush, J. W. M. & Eames, I. 1998 Fluid displacement by high Reynolds number bubble motion in a thin gap. Intl J. Multiphase Flow 24 (3), 411–430.CrossRefGoogle Scholar
Cimbala, J. M., Nagib, H. M. & Roshko, A. 1988 Large structure in the far wakes of two-dimensional bluff bodies. J. Fluid Mech. 190, 265–298.CrossRefGoogle Scholar
Collins, R. 1965 A simple model of the plane gas bubble in a finite liquid. J. Fluid Mech. 22, 763–771.CrossRefGoogle Scholar
Ellingsen, K. & Risso, F. 2001 On the rise of an ellipsoidal bubble in water: oscillatory paths and liquid-induced velocity. J. Fluid Mech. 440, 235–268.Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of freely rising or falling bodies. Annu. Rev. Fluid Mech. 44, 97–121.CrossRefGoogle Scholar
Ern, P., Risso, F., Fernandes, P. C. & Magnaudet, J. 2009 A dynamical model for the buoyancy-driven zigzag motion of oblate bodies. Phys. Rev. Lett. 102, 134505.Google Scholar
Fernandes, P. C., Ern, P., Risso, F. & Magnaudet, J. 2005 On the zigzag dynamics of freely moving axisymmetric bodies. Phys. Fluids 17, 098107.CrossRefGoogle Scholar
Fernandes, P. C., Ern, P., Risso, F. & Magnaudet, J. 2008 Dynamics of axisymmetric bodies rising along a zigzag path. J. Fluid Mech. 606, 209–223.CrossRefGoogle Scholar
Figueroa Espinoza, B., Zenit, R. & Legendre, D. 2008 The effect of confinement on the motion of a single clean bubble. J. Fluid Mech. 616, 419–443.Google Scholar
Filella, A.2015 Mouvement et sillage de bulles isolées ou en interaction confinées entre deux plaques. PhD thesis, Institut National Polytechnique de Toulouse, France.Google Scholar
Gondret, P. & Rabaud, M. 1997 Shear instability of two-fluid parallel flow in a Hele-Shaw cell. Phys. Fluids 9 (11), 3267–3274.Google Scholar
Graftieaux, L., Michard, M. & Grosjean, N. 2001 Combining PIV POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas. Sci. Technol. 12, 1422–1429.Google Scholar
Lazarek, G. M. & Littman, H. 1974 The pressure field due to large circular capped air bubble rising in water. J. Fluid Mech. 66, 673–687.CrossRefGoogle Scholar
Lunde, K. & Perkins, R. J. 1997 Observations on wakes behind spheroidal bubbles and particles. ASME Fluids Eng. Division Summer Meeting paper 97-3530.Google Scholar
Lunde, K. & Perkins, R. J. 1998 Shape oscillations of rising bubbles. In Fascination of Fluid Dynamics, pp. 387–408. Springer.Google Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32, 659–708.Google Scholar
Moore, D. W. 1965 The velocity of rise of distorted gas bubbles in a liquid of small viscosity. J. Fluid Mech. 23, 749–766.CrossRefGoogle Scholar
Mougin, G. & Magnaudet, J. 2002 a The generalized Kirchhoff equations and their application to the interaction between a rigid body and an arbitrary time-dependent viscous flow. Intl J. Multiphase Flow 28, 1837–1851.Google Scholar
Mougin, G. & Magnaudet, J. 2002b Path instability of a rising bubble. Phys. Rev. Lett. 88, 014502.Google Scholar
Mougin, G. & Magnaudet, J. 2006 Wake-induced forces and torques on a zigzagging/spiralling bubble. J. Fluid Mech. 567, 185–194.Google Scholar
Prosperetti, A. 2004 Bubbles. Phys. Fluids 16, 1852–1865.CrossRefGoogle Scholar
Roig, V., Roudet, M., Risso, F. & Billet, A.-M. 2012 Dynamics of a high-Reynolds-number bubble rising within a thin gap. J. Fluid Mech. 707, 444–466.Google Scholar
Roudet, M., Billet, A. M., Risso, F. & Roig, V. 2011 PIV with volume lighting in a narrow cell: An efficient method to measure large velocity fields of rapidly varying flows. Exp. Therm. Fluid Sci. 35 (6), 1030–1037.CrossRefGoogle Scholar
Satijn, M. P., Cense, A. W., Verzicco, R., Clercx, H. J. H. & van Heijst, G. J. F. 2001 Three-dimensional structure and decay properties of vortices in shallow fluid layers. Phys. Fluids 13 (7), 1932.Google Scholar
Shew, W., Poncet, S. & Pinton, J. F. 2006 Force measurements on rising bubbles. J. Fluid Mech. 569, 51–60.CrossRefGoogle Scholar
Tchoufag, J., Magnaudet, J. & Fabre, D. 2014 Linear instability of the path of a freely rising spheroidal bubble. J. Fluid Mech. 751, R4, 1–12.CrossRefGoogle Scholar
Veldhuis, C., Biesheuvel, A. & Van Wijngaarden, L. 2008 Shape oscillations on bubbles rising in clean and in tap water. Phys. Fluids 20 (4), 040705.CrossRefGoogle Scholar
Wang, X., Klaasen, B., Degreve, J., Blanpain, B. & Verhaeghe, F. 2014 Experimental and numerical study of buoyancy-driven single bubble dynamics in a vertical Hele-Shaw cell. Phys. Fluids 26, 123303; doi:10.1063/1.4903488.Google Scholar
Whittaker, E. T. & Watson, G. N. 1927 A Course of Modern Analysis, Cambridge Mathematical Library.Google Scholar
Zenit, R. & Magnaudet, J. 2008 Path instability of spheroidal rising bubbles: a shape-controlled process. Phys. Fluids 20, 061702.Google Scholar
Zenit, R. & Magnaudet, J. 2009 Measurements of the streamwise vorticity in the wake of an oscillating bubble. Intl J. Multiphase Flow 35, 195–203.CrossRefGoogle Scholar