Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-23T23:45:19.486Z Has data issue: false hasContentIssue false
  • English
  • Français

Eigenvalue sensitivity, singular values and discrete frequency selection mechanism in noise amplifiers: the case of flow induced by radial wall injection

Published online by Cambridge University Press:  26 September 2014

Stéphane Cerqueira  and
Denis Sipp
Stéphane Cerqueira*
Affiliation:
ONERA, The French AerospaceLab, 8 rue des Vertugadins, 92190 Meudon, France
Denis Sipp
Affiliation:
ONERA, The French AerospaceLab, 8 rue des Vertugadins, 92190 Meudon, France
*
†Email address for correspondence: stephane.cerqueira@airbus.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We have performed linearized direct numerical simulations (DNS) of flow induced by radial wall injection forced by white-noise Gaussian forcings. We have shown that the frequency spectrum of the flow exhibits low-frequency discrete peaks in the case of a spatial structure of the forcing that is large scale. On the other hand, we observed that the spectrum becomes smooth (with no discrete peaks) if the spatial structure of the forcing is of a smaller extent. We have then tried to analyse these results in the light of global stability analyses. We have first computed the eigenvalue spectrum of the Jacobian and shown that the computed eigenvalues in the frequency range of interest were strongly damped and extremely sensitive to numerical discretization choices if large domains in the axial direction were considered. If shorter domains are used, then the eigenvalues are more robust but still extremely sensitive to the location of the upstream and downstream boundaries. 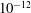Analysis of the $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\epsilon $-pseudo-spectrum showed that eigenvalues located in a region displaying ‘background’ values of $ \epsilon $ below $10^{-12}$ were extremely sensitive and confirmed that all values in this region of the spectrum were actually quasi-eigenvalues. The eigenvalues are therefore ill-behaved and cannot be invoked to explain the observed discrete frequency selection mechanism. We have then performed a singular value decomposition of the global resolvent matrix to compute the leading optimal gains, optimal forcings and optimal responses, which are robust quantities, insensitive to numerical discretization details. We showed that the frequency response of the flow with the large-scale forcing can accurately be reproduced by an approximation based on the leading optimal gain/forcing/response. Analysis of this approximation showed that it is the projection coefficient of the forcing onto the leading optimal forcing that is responsible for the discrete frequency selection mechanism in the case of the large-scale forcing. From a more physical point of view, such a discrete behaviour stems from the streamwise oscillations of the leading optimal forcings, whose wavelengths vary with frequency, in combination with finite extent forcings (which start or end at locations where the leading optimal forcings are strong). Experimental results in the literature are finally discussed in light of these findings.

JFM classification

Instability: Instability Wakes/Jets: Shear layers Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 770 - 799
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akervik, E., Ehrenstein, U., Gallaire, F. & Henningson, D. S. 2008 Global two-dimensional stability measures of the flat plate boundary-layer flow. Eur. J. Mech. (B/Fluids) 27 (5), 501–513.CrossRefGoogle Scholar
Alizard, F. & Robinet, J.-C. 2007 Spatially convective global modes in a boundary layer. Phys. Fluids 19 (11), 114105.CrossRefGoogle Scholar
Amestoy, P. R., Duff, I. S., Koster, J. & L’Excellent, J.-Y. 2001 A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J. Matrix Anal. Applic. 23 (1), 15–41.CrossRefGoogle Scholar
Barbagallo, A., Sipp, D. & Schmid, P. J. 2009 Closed-loop control of an open cavity flow using reduced-order models. J. Fluid Mech. 641, 1–50.CrossRefGoogle Scholar
Barbagallo, A., Sipp, D. & Schmid, P. J. 2011 Input–output measures for model reduction and closed-loop control: application to global modes. J. Fluid Mech. 685, 23–53.CrossRefGoogle Scholar
Blackburn, H. M., Barkley, D. & Sherwin, S. J. 2008 Convective instability and transient growth in flow over a backward-facing step. J. Fluid Mech. 603, 271–304.CrossRefGoogle Scholar
Blesbois, O., Chernyshenko, S. I., Touber, E. & Leschziner, M. A. 2013 Pattern prediction by linear analysis of turbulent flow with drag reduction by wall oscillation. J. Fluid Mech. 724, 607–641.CrossRefGoogle Scholar
Boyer, G., Casalis, G. & Estivalèzes, J. L. 2013a Stability analysis and numerical simulation of simplified solid rocket motors. Phys. Fluids 25, 084109.CrossRefGoogle Scholar
Boyer, G., Casalis, G. & Estivalèzes, J. L. 2013b Stability and sensitivity analysis in a simplified solid rocket motor flow. J. Fluid Mech. 722, 618–644.CrossRefGoogle Scholar
Cantwell, C. D., Barkley, D. & Blackburn, H. M. 2010 Transient growth analysis of flow through a sudden expansion in a circular pipe. Phys. Fluids 22, 034101.CrossRefGoogle Scholar
Casalis, G., Avalon, G. & Pineau, J. P. 1998 Spatial instability of planar channel flow with fluid injection through porous walls. Phys. Fluids 10, 2558–2568.CrossRefGoogle Scholar
Cerqueira, S., Avalon, G. & Feyel, F.2009 An experimental investigation of fluid–structure interaction inside solid propellant rocket motors. AIAA Paper 2009-5427, Proceedings of the AIAA/ASME/SAE/ASEE, 45th Joint Propulsion Conference and Exhibit, Denver, Colorado.CrossRefGoogle Scholar
Chedevergne, F.2007 Instabilités intrinsèques des moteurs à propergol solide. PhD thesis, Ecole Nationale Supérieure de l’Aéronautique et de l’Espace (ENSAE), Toulouse, France.Google Scholar
Chedevergne, F., Casalis, G. & Féraille, T. 2006 Biglobal linear stability analysis of the flow induced by wall injection. Phys. Fluids 18, 014103.CrossRefGoogle Scholar
Chedevergne, F., Casalis, G. & Majdalani, J. 2012 Direct numerical simulation and biglobal stability investigations of the gaseous motion in solid rocket motors. J. Fluid Mech. 706, 190–218.CrossRefGoogle Scholar
Chernyshenko, S. I. & Baig, M. F. 2005 The mechanism of streak formation in near-wall turbulence. J. Fluid Mech. 544, 99–131.CrossRefGoogle Scholar
Crouch, J. D. 1992 Localized receptivity of boundary layers. Phys. Fluids A 4 (7), 1408–1414.CrossRefGoogle Scholar
Culick, F. E. C. 1966 Rotational axisymmetric mean flow and damping of acoustic waves in a solid propellant rocket. AIAA J. 4 (8), 1462–1464.CrossRefGoogle Scholar
Culick, F. E. C.2006 Unsteady motions in combustion chambers for propulsion systems. NATO Science and Technology Organization – RTO AGARDograph RTO-AG-AVT-039 AC/323(AVT-039)TP/103.Google Scholar
Davis, T. A. & Duff, I. S. 1997 An unsymmetric-pattern multifrontal method for sparse LU factorization. SIAM J. Matrix Anal. Applics. 18 (1), 140–158.CrossRefGoogle Scholar
Dergham, G., Sipp, D. & Robinet, J.-C. 2013 Stochastic dynamics and model reduction of amplifier flows: the backward facing step flow. J. Fluid Mech. 719, 406–430.CrossRefGoogle Scholar
Dunlap, R., Blackner, A. M., Waugh, R. C., Brown, R. S. & Willoughby, P. G. 1990 Internal flow field studies in a simulated cylindrical port rocket chamber. J. Propul. Power 6 (6), 690–704.CrossRefGoogle Scholar
Ehrenstein, U. & Gallaire, F. 2005 On two-dimensional temporal modes in spatially evolving open flows: the flat-plate boundary layer. J. Fluid Mech. 536, 209–218.CrossRefGoogle Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013a Modal and transient dynamics of jet flows. Phys. Fluids 25 (4), 044103.CrossRefGoogle Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013b The preferred mode of incompressible jets: linear frequency response analysis. J. Fluid Mech. 716, 189–202.CrossRefGoogle Scholar
Griffond, J., Casalis, G. & Pineau, J. P. 2000 Spatial instability of flow in a semiinfinite cylinder with fluid injection through its porous walls. Eur. J. Mech. (B/Fluids) 19, 69–87.CrossRefGoogle Scholar
Ilak, M., Schlatter, P., Bagheri, S. & Henningson, D. S. 2012 Bifurcation and stability analysis of a jet in cross-flow: onset of global instability at a low velocity ratio. J. Fluid Mech. 696, 94–121.CrossRefGoogle Scholar
Majdalani, J. & Van Moorhem, W. 1998 Improved time-dependent flowfield solution for solid rocket motors. AIAA J. 36 (2), 241–248.CrossRefGoogle Scholar
Marquet, O., Lombardi, M., Chomaz, J.-M., Sipp, D. & Jacquin, L. 2009 Direct and adjoint global modes of a recirculation bubble: lift-up and convective non-normalities. J. Fluid Mech. 622, 1–21.CrossRefGoogle Scholar
Marquet, O., Sipp, D., Chomaz, J.-M. & Jacquin, L. 2008 Amplifier and resonator dynamics of a low-Reynolds-number recirculation bubble in a global framework. J. Fluid Mech. 605, 429–443.CrossRefGoogle Scholar
Matsumoto, J. & Kawahara, M. 2000 Stable shape identification for fluid–structure interaction problem using mini element. Trans. ASME J. Appl. Mech. 3, 263–274.CrossRefGoogle Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
Moarref, R. & Jovanović, M. R. 2012 Model-based design of transverse wall oscillations for turbulent drag reduction. J. Fluid Mech. 707, 205–240.CrossRefGoogle Scholar
Monokrousos, A., Akervik, E., Brandt, L. & Henningson, D. S. 2010 Global three-dimensional optimal disturbances in the blasius boundary-layer flow using time-steppers. J. Fluid Mech. 650, 181–214.CrossRefGoogle Scholar
Orr, W. M. F. 1907 Stability or instability of the steady motions of a perfect liquid. Proc. R. Irish Acad. 27, 9–69.Google Scholar
Sanmiguel-Rojas, E., del Pino, C. & Gutierrez-Montes, C. 2010 Global mode analysis of a pipe flow through a 1:2 axisymmetric sudden expansion. Phys. Fluids 22 (7), 071702.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Sharma, A. S. & McKeon, B. J. 2013 On coherent structure in wall turbulence. J. Fluid Mech. 728, 196–238.CrossRefGoogle Scholar
Sipp, D. & Marquet, O. 2012 Characterization of noise amplifiers with global singular modes: the case of the leading-edge flat-plate boundary layer. Theor. Comput. Fluid Dyn. 27, 617–635.CrossRefGoogle Scholar
Sipp, D., Marquet, O., Meliga, O. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open flows: a linearized approach. Appl. Mech. Rev. 63, 030801.CrossRefGoogle Scholar
Taylor, G. I. 1956 Fluid flow in regions bounded by porous surfaces. Proc. R. Soc. Lond. 234, 456–475.Google Scholar
Trefethen, L. N. & Embree, M. 2005 Spectra and Pseudospectra: The Behavior of Non-normal Matrices and Operators. Princeton University Press.CrossRefGoogle Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.CrossRefGoogle ScholarPubMed
Varapaev, V. N. & Yagodkin, V. I. 1969 Flow stability in a channel with porous walls. Izv. Akad. Nauk SSSR Mekh. Zhidk. Gaza 4 (5), 91–95.Google Scholar
Vuillot, F. 1995 Vortex shedding phenomena in solid rocket motors. J. Propul. Power 11, 626–639.CrossRefGoogle Scholar
Supplementary material: PDF

Cerqueira and Sipp supplementary material

Supplementary material

Download Cerqueira and Sipp supplementary material(PDF)
PDF 130 KB