Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-17T07:11:13.486Z Has data issue: false hasContentIssue false
  • English
  • Français

The planar X-junction flow: stability analysis and control

Published online by Cambridge University Press:  16 July 2014

Iman Lashgari ,
Outi Tammisola ,
Vincenzo Citro ,
Matthew P. Juniper  and
Luca Brandt
Iman Lashgari
Affiliation:
Linné FLOW Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden
Outi Tammisola*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
Vincenzo Citro
Affiliation:
DIIN, University of Salerno, via Ponte don Melillo, 84084 Fisciano (SA), Italy
Matthew P. Juniper
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
Luca Brandt
Affiliation:
Linné FLOW Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: outi@mech.kth.se
Get access Rights & Permissions [Opens in a new window]

Abstract

The bifurcations and control of the flow in a planar X-junction are studied via linear stability analysis and direct numerical simulations. This study reveals the instability mechanisms in a symmetric channel junction and shows how these can be stabilized or destabilized by boundary modification. We observe two bifurcations as the Reynolds number increases. They both scale with the inlet speed of the two side channels and are almost independent of the inlet speed of the main channel. Equivalently, both bifurcations appear when the recirculation zones reach a critical length. A two-dimensional stationary global mode becomes unstable first, changing the flow from a steady symmetric state to a steady asymmetric state via a pitchfork bifurcation. The core of this instability, whether defined by the structural sensitivity or by the disturbance energy production, is at the edges of the recirculation bubbles, which are located symmetrically along the walls of the downstream channel. The energy analysis shows that the first bifurcation is due to a lift-up mechanism. We develop an adjustable control strategy for the first bifurcation with distributed suction or blowing at the walls. The linearly optimal wall-normal velocity distribution is computed through a sensitivity analysis and is shown to delay the first bifurcation from 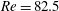$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}=82.5$ to 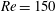$\mathit{Re}=150$. This stabilizing effect arises because blowing at the walls weakens the wall-normal gradient of the streamwise velocity around the recirculation zone and hinders the lift-up. At the second bifurcation, a three-dimensional stationary global mode with a spanwise wavenumber of order unity becomes unstable around the asymmetric steady state. Nonlinear three-dimensional simulations at the second bifurcation display transition to a nonlinear cycle involving growth of a three-dimensional steady structure, time-periodic secondary instability and nonlinear breakdown restoring a two-dimensional flow. Finally, we show that the sensitivity to wall suction at the second bifurcation is as large as it is at the first bifurcation, providing a possible mechanism for destabilization.

JFM classification

Flow Control: Flow Control Instability: Instability Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 753 , 25 August 2014 , pp. 1 - 28
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

The original version of this article was published with incorrect affiliations for O. Tammisola, V. Citro and M. P. Juniper. A notice detailing this has been published online and in print, and the error rectified in the print and the online PDF and HTML copies.

References

Albensoeder, S., Kuhlmann, H. C. & Rath, H. J. 2001 Three-dimensional centrifugal-flow instabilities in the lid-driven-cavity problem. Phys. Fluids 13, 121–135.Google Scholar
Barkley, D., Blackburn, H. M. & Sherwin, S. J. 2008 Direct optimal growth analysis for timesteppers. Intl J. Numer. Meth. Fluids 57, 1435–1458.Google Scholar
Barkley, D., Gomes, G. M. & Henderson, R. D. 2002 Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech. 473, 167–190.CrossRefGoogle Scholar
Best, J. L. 1987 Flow dynamics at river channel confluences: implications for sediment transport and bed morphology. In Recent Developments of Fluvial Sedimentology, pp. 27–35. Society of Economic Paleontologists and Mineralogists.CrossRefGoogle Scholar
Best, J. L. & Reid, I. 1984 Separation zone at open-channel junctions. J. Hydraul. Engng ASCE 110, 1588–1594.Google Scholar
Bourque, C. & Newman, B. G. 1960 Reattachment of a two-dimensional, incompressible jet to an adjacent flat plate. Aeronaut. Q. 11, 201–232.Google Scholar
Brandt, L. 2014 The lift-up effect: the linear mechanism behind transition and turbulence in shear flows. Eur. J. Mech. (B/Fluids) 47, 80–96.Google Scholar
Cherdron, W., Durst, F. & Whitelaw, J. H. 1978 Asymmetric flows and instabilities in symmetric ducts with sudden expansion. J. Fluid Mech. 84, 13–31.Google Scholar
Chiang, T. & Sheu, T. W. H. 2002 Bifurcations of flow through plane symmetric channel contraction. Trans. ASME: J. Fluids Engng 124, 444–451.Google Scholar
Chomaz, J. M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
Fani, A., Camarri, S. & Salvetti, M. V. 2012 Stability analysis and control of the flow in a symmetric channel with a sudden expansion. Phys. Fluids 24, 084102.Google Scholar
Fani, A., Camarri, S. & Salvetti, M. V. 2013 Investigation of the steady engulfment regime in a three-dimensional T-mixer. Phys. Fluids 25, 064102.Google Scholar
Fearn, R. M., Mullin, T. & Cliffe, K. A. 1990 Nonlinear flow phenomena in a symmetric sudden expansion. J. Fluid Mech. 211, 595–608.CrossRefGoogle Scholar
Gallaire, F., Marquillie, M. & Ehrenstein, U. 2007 Three-dimensional transverse instabilities in detached boundary layer. J. Fluid Mech. 571, 221–223.CrossRefGoogle Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
Håkansson, K.2012 Orientation of elongated particles in shear and extensional flow. Licentiate thesis in Engineering Mechanics, Stockholm, Sweden.Google Scholar
Håkansson, K., Fall, A., Lundell, F., Yu, S., Krywka, C., Roth, S. V., Santoro, G., Kvick, M., Prahl-Wittberg, L., Wågberg, L. & Söderberg, L. D. 2014 Hydrodynamic alignment and assembly of nanofibrils resulting in strong cellulose filaments. Nat. Commun. 5, 4018.Google Scholar
Haque, S., Lashgari, I., Giannetti, F. & Brandt, L. 2012 Stability of fluids with shear-dependent viscosity in the lid-driven cavity. J. Non-Newtonian Fluid Mech. 173, 49–61.Google Scholar
Hill, D. C.1992 A theoretical approach for analyzing the re-stabilization of wake. AIAA Paper 92-0067.CrossRefGoogle Scholar
Joanicot, M. & Ajdari, A. 2005 Droplet control for microfluidics. Science 309, 887–888.Google Scholar
Kinahan, M. E., Filippidi, E., Köster, S., Hu, X., Evans, H. M., Pfohl, T., Kaplan, D. L. & Wong, J. 2011 Tunable silk: using microfluidics to fabricate silk fibers with controllable properties. Biomacromolecules 12, 1504–1511.Google Scholar
Kockmann, N., Foll, C. & Woias, P. 2003 Flow regimes and mass transfer characteristics in static micromixers. Proc. SPIE 4982, 319–329.CrossRefGoogle Scholar
Landahl, M. T. 1975 Dynamics and control of global instabilities in open flows: a linearized approach. SIAM J. Appl. Maths 28, 735–756.Google Scholar
Lanzerstorfer, D. & Kuhlmann, H. 2011 Global stability of the two-dimensional flow over a backward-facing step. J. Fluid Mech. 693, 1–27.Google Scholar
Lanzerstorfer, D. & Kuhlmann, H. C. 2012 Global stability of multiple solutions in plane sudden-expansion flow. J. Fluid Mech. 702, 378–402.Google Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46, 493–517.Google Scholar
Maday, Y. & Patera, A. T. 1989 Spectral element methods for the Navier–Stokes equations. In State-of-the-Art Surveys in Computational Mechanics (ed. Noor, A. K.), vol. 18, pp. 71–143. ASME.Google Scholar
Marquet, O., Lombardi, M., Chomaz, J. M., Sipp, D. & Jacquin, L. 2009 Direct and adjoint global modes of a recirculation bubble: lift-up and convective non-normalities. J. Fluid Mech. 622, 1–21.Google Scholar
Marquet, O. & Sipp, D. 2010 Active, steady control of vortex shedding: an adjoint-based sensitivity approach. In Seventh IUTAM Symposium on Laminar–Turbulent Transition, IUTAM Bookseries, vol. 18, pp. 259–264. Springer.Google Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.Google Scholar
Meliga, P. & Chomaz, J. M. 2011 Global modes in a confined impinging jet: application to heat transfer and control. Theor. Comput. Fluid Dyn. 25, 179–193.Google Scholar
Mizushima, J. & Shiotani, Y. 2000 Transitions and instabilities of flow in a symmetric channel with a suddenly expanded and contracted part. J. Fluid Mech. 434, 355–369.Google Scholar
Nguyen, N. G. & Wu, Z. 2005 Micromixers – a review. J. Micromech. Microengng 15, R1.Google Scholar
Oliveira, M. S. N., Pinho, F. T. & Alves, M. A. 2012 Divergent streamlines and free vortices in Newtonian fluid flows in microfluidic flow-focusing devices. J. Fluid Mech. 711, 171–191.Google Scholar
Passaggia, P. Y., Leweke, T. & Ehrenstein, U. 2012 Transverse instability and low-frequency flapping in incompressible separated boundary layer flows: an experimental study. J. Fluid Mech. 703, 363–373.Google Scholar
Patera, A. T. 1984 A spectral element method for fluid dynamics: laminar flow in a channel expansion. J. Comput. Phys. 54, 468–488.Google Scholar
Pironneau, O., Hecht, F. & Morice, J.2013 FreeFEM $++$ . Available at: http://www.freefem.org.Google Scholar
Poole, R. J., Alves, M. A. & Oliveira, P. J. 2007 Purely elastic flow asymmetries. Phys. Rev. Lett. 99, 164503.CrossRefGoogle ScholarPubMed
Poole, R. J., Rocha, G. N. & Oliveira, P. J. 2014 A symmetry-breaking inertial bifurcation in a cross-slot flow. Comput. Fluids 93, 164503.CrossRefGoogle Scholar
Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.CrossRefGoogle Scholar
Rodriguez, D. & Theofilis, V. 2010 Structural changes of laminar separation bubbles induced by global linear instability. J. Fluid Mech. 655, 280–305.CrossRefGoogle Scholar
Shabayek, S., Steffler, P. & Hicks, F. 2002 Dynamic model for subcritical combining flows in channel junctions. J. Hydraul. Engng ASCE 128, 821–828.Google Scholar
Sherwin, S. J. & Blackburn, H. M. 2005 Three-dimensional instabilities and transition of steady and pulsatile axisymmetric stenotic flows. J. Fluid Mech. 533, 297–327.CrossRefGoogle Scholar
Sipp, D., Marquet, O., Meliga, P. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open flows: a linearized approach. Appl. Mech. Rev. 63, 030801.Google Scholar
Sobey, I. J. & Drazin, P. G. 1986 Bifurcations of the two-dimensional channel flows. J. Fluid Mech. 171, 263–287.Google Scholar
Tomas, S., Ameel, T. & Guilkey, J. 2010 Mixing kinematics of moderate Reynolds number flows in a T-channel. Phys. Fluids 22, 013601.Google Scholar
Tufo, H. M. & Fischer, P. F. 1999 Terascale spectral element algorithms and implementations. In Proceedings of the 1999 ACM/IEEE Conference on Supercomputing. ACM.Google Scholar