Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-19T05:59:26.962Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of complex singularities in high-Reynolds-number Navier–Stokes solutions

Published online by Cambridge University Press:  17 April 2014

F. Gargano ,
M. Sammartino ,
V. Sciacca  and
K. W. Cassel
F. Gargano
Affiliation:
Department of Mathematics, University of Palermo, Palermo, Italy
M. Sammartino*
Affiliation:
Department of Mathematics, University of Palermo, Palermo, Italy
V. Sciacca
Affiliation:
Department of Mathematics, University of Palermo, Palermo, Italy
K. W. Cassel
Affiliation:
Fluid Dynamics Research Centre, Department of Mechanical, Materials, and Aerospace Engineering, Illinois Institute of Technology, Chicago, IL 60616, USA
*
†Email address for correspondence: marco@math.unipa.it
Get access Rights & Permissions [Opens in a new window]

Abstract

Numerical solutions of the laminar Prandtl boundary-layer and Navier–Stokes equations are considered for the case of the two-dimensional uniform flow past an impulsively-started circular cylinder. The various viscous–inviscid interactions that occur during the unsteady separation process are investigated by applying complex singularity analysis to the wall shear and streamwise velocity component of the two solutions. This is carried out using two different methodologies, namely a singularity-tracking method and the Padé approximation. It is shown how the van Dommelen and Shen singularity that occurs in solutions of the Prandtl boundary-layer equations evolves in the complex plane before leading to a separation singularity in finite time. Navier–Stokes solutions, computed at different Reynolds numbers in the range 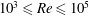$10^3 \leq Re \leq 10^5$, are characterized by the presence of various complex singularities that can be related to different physical interactions acting over multiple spatial scales. The first interaction developing in the separation process is large-scale interaction that is visible for all the Reynolds numbers considered, and it signals the first relevant differences between the Prandtl and Navier–Stokes solutions. For 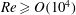$Re\geq O(10^4)$, a small-scale interaction follows the large-scale interaction. The onset of these interactions is related to the characteristic changes of the streamwise pressure gradient on the circular cylinder. Even if these interactions physically differ from that prescribed by the Prandtl solution, and they set a possible limit on the comparison of Prandtl solutions with Navier–Stokes solutions, it is shown how the asymptotic validity of boundary-layer theory is strongly supported by the results that have been obtained through the complex singularity analysis.

JFM classification

Boundary Layers: Boundary layer separation Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 747 , 25 May 2014 , pp. 381 - 421
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bailey, D. H., Yozo, H., Li, X. S. & Thompson, B.2002 ARPREC: an arbitrary precision computation package Lawrence Berkeley National Laboratory. Paper LBNL-53651.Google Scholar
Baker, G. A. & Graves-Morris, P. 1996 Padé Approximants. Cambridge University Press.Google Scholar
Blasius, H. 1908 Grenzschichten in Flussigketein mit kleiner Reibung. Z. Math. Phys. 56, 1–37.Google Scholar
Bowles, R. I. 2006 Lighthill and the triple-deck, separation and transition. J. Engng Maths 56, 445–460.Google Scholar
Bowles, R. I., Davies, C. & Smith, F. T. 2003 On the spiking stages in deep transition and unsteady separation. J. Engng Maths 45, 227–245.CrossRefGoogle Scholar
Brinckman, K. W. & Walker, J. D. A. 2002 Instability in a viscous flow driven by streamwise vortices. J. Fluid Mech. 432, 127–166.Google Scholar
Caflisch, R. E. 1993 Singularity formation for Caflisch complex solutions of the 3D incompressible Euler equations. Physica D 67, 1–18.Google Scholar
Caflisch, R. & Sammartino, M. 1997 Navier–Stokes equations on an exterior circular domain: construction of the solution and the zero viscosity limit. C. R. Acad. Sci. Ser. I – Math. 324 (8), 861–866.Google Scholar
Caflisch, R. E. & Sammartino, M. 2000 Existence and singularities for the Prandtl boundary layer equations. Z. Angew. Math. Mech. 80 (11–12), 733–744 (Special issue on the occasion of the 125th anniversary of the birth of Ludwig Prandtl).Google Scholar
Cannone, M., Lombardo, M. C. & Sammartino, M. 2013 Well-posedness of Prandtl equations with non-compatible data. Nonlinearity 26 (3), 3077–3100.Google Scholar
Carrier, G. F., Krook, M. & Pearson, C. E. 1966 Functions of A Complex Variable: Theory and Technique. McGraw-Hill.Google Scholar
Cassel, K. W. 2000 A comparison of Navier–Stokes solutions with the theoretical description of unsteady separation. Phil. Trans. R. Soc. Lond. A 358, 3207–3227.Google Scholar
Cassel, K. W. & Obabko, A. V. 2010 A Rayleigh instability in a vortex-induced unsteady boundary layer. Phys. Scr. 2010 (T142), 014006.Google Scholar
Chapman, D. R., Kuehn, D. M. & Larson, H. K.1958 Investigation of separated flows in supersonic and subsonic streams with emphasis on the effect of transition NACA Rep. (1356).Google Scholar
Cheng, W. & Wang, X. 2007 Discrete Kato-type theorem on inviscid limit of Navier–Stokes flows. J. Math. Phys. 48 (1), 065303.Google Scholar
Clercx, H. J. H. & Bruneau, C. -H. 2006 The normal and oblique collision of a dipole with a no-slip boundary. Comput. Fluids 35 (3), 245–279.Google Scholar
Clercx, H. J. H. & van Heijst, G. J. F. 2002 Dissipation of kinetic energy in two-dimensional bounded flows. Phys. Rev. E 65 (6), 066305.CrossRefGoogle ScholarPubMed
Clopeau, T., Mikelic, A. & Robert, R. 1998 On the vanishing viscosity limit for the 2D incompressible Navier–Stokes equations with the friction type boundary conditions. Nonlinearity 11 (6), 1625–1636.Google Scholar
Coclite, G. M., Gargano, F. & Sciacca, V. 2012 Analytic solutions and singularity formation for the peakon b-family equations. Acta Appl. Maths 122, 419–434.Google Scholar
Cowley, S. J. 1983 Computer extension and analytic continuation of Blasius’ expansion for impulsive flow past a circular cylinder. J. Fluid Mech. 135, 389–405.Google Scholar
Cowley, S. J.2001 Laminar boundary-layer theory: a 20th century paradox? Proceedings of ICTAM 2000 pp. 389–411.Google Scholar
Cowley, S. J., Baker, G. R. & Tanveer, S. 1999 On the formation of Moore curvature singularities in vortex sheets. J. Fluid Mech. 378, 233–267.Google Scholar
Della Rocca, G., Lombardo, M. C., Sammartino, M. & Sciacca, V. 2006 Singularity tracking for Camassa–Holm and Prandtl’s equations. Appl. Numer. Maths 56 (8), 1108–1122.Google Scholar
Doligalski, T. L. & Walker, J. D. A. 1984 The boundary layer induced by a convected two-dimensianal vortex. J. Fluid Mech. 139, 1–28.CrossRefGoogle Scholar
E, W. 2000 Boundary layer theory and the zero-viscosity limit of the Navier–Stokes equation. Acta Math. Sin. 16, 207–218.Google Scholar
E, W. & Engquist, B. 1997 Blowup of the solutions to the unsteady Prandtl’s equations. Commun. Pure Appl. Maths 50 (12), 1287–1293.Google Scholar
Elliott, J. W., Smith, F. T. & Cowley, S. J. 1983 Breakdown of boundary layers: (I) on moving surfaces; (II) in semisimilar unsteady flow; (III) in fully unsteady flow. Geophys. Astrophys. Fluid Dyn. 25 (1–2), 77–138.Google Scholar
Frisch, U., Matsumoto, T. & Bec, J. 2003 Singularities of Euler flow? Not out of the blue! J. Stat. Phys. 113, 761–781.Google Scholar
Gargano, F., Sammartino, M. & Sciacca, V. 2009 Singularity formation for Prandtl’s equations. Physica D 238 (19), 1975–1991.Google Scholar
Gargano, F., Sammartino, M. & Sciacca, V. 2011 High Reynolds number Navier–Stokes solutions and boundary layer separation induced by a rectilinear vortex. Comput. Fluids 52, 73–91.Google Scholar
Goldstein, R. E., Pesci, A. I. & Shelley, M. J. 1998 Instabilities and singularities in Hele–Shaw flow. Phys. Fluids 10 (11), 2701–2723.Google Scholar
Grenier, E. 2000 On the stability of boundary layers of incompressible Euler equations. J. Differ. Equ. 164, 180–222.CrossRefGoogle Scholar
Hoyle, J. M., Smith, F. T. & Walker, J. D. A. 1991 On sublayer eruption and vortex formation. Comput. Phys. Commun. 65, 151–157.Google Scholar
Iftimie, D. & Planas, G. 2006 Inviscid limits for the Navier–Stokes equations with Navier friction boundary conditions. Nonlinearity 19, 899–918.CrossRefGoogle Scholar
Kato, T. 1984 Remarks on zero viscosity limit for nonstationary Navier–Stokes flows with boundary. In Seminar on Partial Differential Equations., Math. Sci. Res. Inst. Publ., pp. 85–98.Google Scholar
Kelliher, J. P. 2006 Navier–Stokes equations with Navier boundary conditions for bounded domain in the plane. J. Math. Anal. 38, 210–232.Google Scholar
Kelliher, J. P. 2007 On Kato’s conditions for vanishing viscosity. Indiana Univ. Math. J. 56 (4), 1711–1721.Google Scholar
Kramer, W., Clercx, H. J. H. & van Heijst, G. J. F. 2007 Vorticity dynamics of a dipole colliding with a no-slip wall. Phys. Fluids 19 (12), 126603.Google Scholar
Kukavica, I. & Vicol, V. 2013 On the local existence of analytic solutions to the Prandtl boundary layer equations. Commun. Math. Sci. 11, 269–292.Google Scholar
Li, L., Walker, J. D. A., Bowles, R. I. & Smith, F. T. 1998 Short-scale break-up in unsteady interactive layers: local development of normal pressure gradients and vortex wind-up. J. Fluid Mech. 374, 335–378.Google Scholar
Lombardo, M. C., Caflisch, R. E. & Sammartino, M. 2001 Asymptotic analysis of the linearized Navier–Stokes equation on an exterior circular domain: explicit solution and the zero viscosity limit. Commun. Part. Diff. Equ. 26 (1–2), 335–354.Google Scholar
Lombardo, M. C., Cannone, M. & Sammartino, M. 2003 Well-posedness of the boundary layer equations. SIAM J. Math. Anal. 35 (4), 987–1004 (electronic).Google Scholar
Lopes Filho, M. C., Mazzucato, A. L. & Nussenzveig Lopes, H. J. 2008 Vanishing viscosity limit for incompressible flow inside a rotating circle. Physica D 237 (10–12), 1324–1333.Google Scholar
Lopes Filho, M. C., Nussenzveig Lopes, H. & Planas, G. 2005 On the inviscid limit for two-dimensional incompressible flow with Navier friction condition. SIAM J. Math. Anal. 36 (4), 1130–1141.Google Scholar
Matsumoto, T., Bec, J. & Frisch, U. 2005 The analytic structure of 2D Euler flow at short times. Fluid Dyn. Res. 36 (4–6), 221–237.Google Scholar
Obabko, A. V. & Cassel, K. W. 2002 Navier–Stokes solutions of unsteady separation induced by a vortex. J. Fluid Mech. 465, 99–130.Google Scholar
Obabko, A. V. & Cassel, K. W. 2005 On the ejection-induced instability in Navier–Stokes solutions of unsteady separation. Phil. Trans. R. Soc. A 363 (1830), 1189–1198.CrossRefGoogle ScholarPubMed
Oleinik, O. A. & Samokhin, V. N. 1999 Mathematical Models in Boundary Layer Theory, Applied Mathematics and Mathematical Computation, vol. 15. Chapman & Hall/CRC.Google Scholar
Orlandi, P. 1990 Vortex dipole rebound from a wall. Phys. Fluids A 2 (8), 1429–1436.Google Scholar
Pauls, W. & Frisch, U. 2007 A Borel transform method for locating singularities of Taylor and Fourier series. J. Stat. Phys. 127 (6), 1095–1119.Google Scholar
Pauls, W., Matsumoto, T., Frisch, U. & Bec, J. 2006 Nature of complex singularities for the 2D Euler equation. Physica D 219 (1), 40–59.Google Scholar
Peridier, V. J., Smith, F. T. & Walker, J. D. A. 1991a Vortex-induced boundary-layer separation. Part 1. The unsteady limit problem $Re\rightarrow \infty $ . J. Fluid Mech. 232, 99–131.Google Scholar
Peridier, V. J., Smith, F. T. & Walker, J. D. A. 1991b Vortex-induced boundary-layer separation. Part 2. Unsteady interacting boundary-layer theory. J. Fluid Mech. 232, 131–165.Google Scholar
Peyret, R. 2002 Spectral Methods for Incompressible Viscous Flow. Springer.CrossRefGoogle Scholar
Sammartino, M. & Caflisch, R. E. 1998a Zero viscosity limit for analytic solutions, of the Navier–Stokes equation on a half-space. I. Existence for Euler and Prandtl equations. Commun. Math. Phys. 192 (2), 433–461.Google Scholar
Sammartino, M. & Caflisch, R. E. 1998b Zero viscosity limit for analytic solutions of the Navier–Stokes equation on a half-space. II. Construction of the Navier–Stokes solution. Commun. Math. Phys. 192 (2), 463–491.Google Scholar
Scheichl, B., Kluwick, A. & Smith, F. T. 2011 Break-away separation for high turbulence intensity and large Reynolds number. J. Fluid Mech. 670, 260–300.Google Scholar
Shelley, M. J. 1992 A study of singularity formation in vortex–sheet motion by a spectrally accurate vortex method. J. Fluid Mech. 244, 493–526.Google Scholar
Smith, F. T. 1988 Finite-time break-up can occur in any unsteady interacting boundary layer. Mathematika 35, 256–273.Google Scholar
Smith, F. T. & Bodonyi, R. J. 1985 On short-scale inviscid instabilities in flow past surface-mounted obstacles and other non-parallel motions. Aeronaut. J. 89, 205–212.Google Scholar
Smith, F. T., Bowles, R. I. & Walker, J. D. A. 2000 Wind-up of a spanwise vortex in deepening transition and stall. J. Theor. Comput. Fluid Dyn. 14, 135–165.CrossRefGoogle Scholar
Sulem, C., Sulem, P. L. & Frisch, H. 1983 Tracing complex singularities with spectral methods. J. Comput. Phys. 50, 138–161.Google Scholar
Temam, R. & Wang, X. 1997 The convergence of the solutions of the Navier–Stokes equations to that of the Euler equations. Appl. Maths Lett. 10, 29–33.Google Scholar
Tutty, O. R. & Cowley, S. J. 1986 On the stability and the numerical solution of the unsteady interactive boundary-layer equation. J. Fluid Mech. 168, 431–456.Google Scholar
van der Hoeven, J. 2009 Algorithms for asymptotic extrapolation. J. Symb. Comput. 44 (8), 1000–1016.Google Scholar
van Dommelen, L. L. & Shen, S. F. 1980 The spontaneous generation of the singularity in a separating laminar boundary layer. J. Comput. Phys. 38, 125–140.Google Scholar
Weideman, J. A. C. 2003 Computing the dynamics of complex singularities of nonlinear PDEs. J. Appl. Dyn. Syst. 2 (2), 171–186.Google Scholar