Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-23T07:16:35.942Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing separable isogenies in quasi-optimal time

Part of: Arithmetic algebraic geometry Abelian varieties and schemes

Published online by Cambridge University Press:  01 February 2015

David Lubicz  and
Damien Robert
David Lubicz
Affiliation:
Université de Rennes 1, Campus de Beaulier, 35042 Rennes, France email david.lubicz@univ-rennes1.fr
Damien Robert
Affiliation:
INRIA Bordeaux Sud-Ouest, 200 avenue de la Vieille Tour, 33405 Talence, France email damien.robert@inria.fr

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 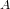$A$ be an abelian variety of dimension $g$ together with a principal polarization 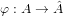${\it\phi}:A\rightarrow \hat{A}$ defined over a field $k$. Let 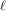$\ell$ be an odd integer prime to the characteristic of $k$ and let 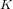$K$ be a subgroup of 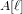$A[\ell ]$ which is maximal isotropic for the Riemann form associated to ${\it\phi}$. We suppose that 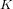$K$ is defined over $k$ and let 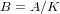$B=A/K$ be the quotient abelian variety together with a polarization compatible with ${\it\phi}$. Then 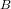$B$, as a polarized abelian variety, and the isogeny 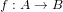$f:A\rightarrow B$ are also defined over $k$. In this paper, we describe an algorithm that takes as input a theta null point of 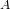$A$ and a polynomial system defining 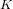$K$ and outputs a theta null point of 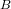$B$ as well as formulas for the isogeny 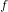$f$. We obtain a complexity of 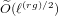$\tilde{O} (\ell ^{(rg)/2})$ operations in $k$ where 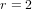$r=2$ (respectively, 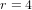$r=4$) if 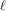$\ell$ is a sum of two (respectively, four) squares which constitutes an improvement over the algorithm described in Cosset and Robert (Math. Comput. (2013) accepted for publication). We note that the algorithm is quasi-optimal if $\ell$ is a sum of two squares since its complexity is quasi-linear in the degree of $f$.

MSC classification

Primary: 14K02: Isogeny 14K25: Theta functions 11G10: Abelian varieties of dimension $> 1$
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 18 , Issue 1 , 2015 , pp. 198 - 216
Copyright
© The Author(s) 2015 

References

Atkin, A., ‘The number of points on an elliptic curve modulo a prime’, manuscript, Chicago, IL, 1988.Google Scholar
Bardet, M., ‘Étude des systèmes algébriques surdéterminés. Applications aux codes correcteurs et à la cryptographie’, PhD Thesis, Université Paris 6, 2004.Google Scholar
Becker, E., Mora, T., Marinari, M. G. and Traverso, C., ‘The shape of the shape lemma’, Proceedings of the International Symposium on Symbolic and Algebraic Computation (ACM Press, 1994) 129–133.Google Scholar
Birkenhake, C. and Lange, H., Complex abelian varieties , 2nd edn, Grundlehren der Mathematischen Wissenschaften, Fundamental Principles of Mathematical Sciences 302 (Springer, Berlin, 2004).Google Scholar
Bisson, G., Cosset, R. and Robert, D., ‘AVIsogenies (Abelian Varieties and Isogenies). Magma package for explicit isogeny computation between abelian varieties’, 2010, http://avisogenies.gforge.inria.fr/.Google Scholar
Bisson, G. and Streng, M., ‘On polarised class groups of orders in quartic cm-fields’, Preprint, 2013, arXiv:1302.3756.Google Scholar
Bisson, G. and Sutherland, A. V., ‘Computing the endomorphism ring of an ordinary elliptic curve over a finite field’, J. Number Theory 131 (2011) no. 5, 815–831.Google Scholar
Bostan, A., Morain, F., Salvy, B. and Schost, E., ‘Fast algorithms for computing isogenies between elliptic curves’, Math. Comput. 77 (2008) no. 263, 1755–1778.Google Scholar
Bröker, R., Lauter, K. and Sutherland, A. V., ‘Modular polynomials via isogeny volcanoes’, Math. Comp. 81 (2012) 1201–1231, doi:10.1090/S0025-5718-2011-02508-1.Google Scholar
Cohen, H., Frey, G., Avanzi, R., Doche, C., Lange, T., Nguyen, K. and Vercauteren, F. (eds), Handbook of elliptic and hyperelliptic curve cryptography , Discrete Mathematics and its Applications (Chapman and Hall/CRC, Boca Raton, FL, 2006).Google Scholar
Cosset, R. and Robert, D., ‘An algorithm for computing (ℓ, ℓ)-isogenies in polynomial time on Jacobians of hyperelliptic curves of genus 2’, Math. Comput. (2013) accepted for publication.Google Scholar
Elkies, N., ‘Explicit isogenies’, manuscript, Boston, 1992.Google Scholar
Faugère, J. C., Gianni, P., Lazard, D. and Mora, T., ‘Efficient computation of zero-dimensional Gröbner bases by change of ordering’, J. Symbolic Comput. 16 (1993) no. 4, 329–344.Google Scholar
Faugère, J.-C., Lubicz, D. and Robert, D., ‘Computing modular correspondences for abelian varieties’, J. Algebra. 343 (2011) 248–277.Google Scholar
Fouquet, M. and Morain, F., ‘Isogeny volcanoes and the SEA algorithm’, Algorithmic number theory (Sydney, 2002) , Lecture Notes in Computer Science 2369 (Springer, Berlin, 2002) 276–291.Google Scholar
Gaudry, P. and Schost, É., ‘Construction of secure random curves of genus 2 over prime fields’, Advances in Cryptology – EUROCRYPT 2004 , Lecture Notes in Computer Science 3027 (eds Cachin, C. and Camenisch, J.; Springer, 2004) 239–256.Google Scholar
Igusa, J.-I., Theta functions , Die Grundlehren der mathematischen Wissenschaften, Band 194 (Springer, New York, 1972).CrossRefGoogle Scholar
Kohel, D., ‘Endomorphism rings of elliptic curves over finite fields’, PhD Thesis, University of California, 1996.Google Scholar
Koizumi, S., ‘Theta relations and projective normality of Abelian varieties’, Amer. J. Math. 98 (1976) no. 4, 865–889.Google Scholar
Lazard, D., ‘Gröbner bases, Gaussian elimination and resolution of systems of algebraic equations’, Computer algebra (London, 1983) , Lecture Notes in Computer Science 162 (Springer, Berlin, 1983) 146–156.Google Scholar
Lazard, D., ‘Ideal bases and primary primary decomposition: case of two variables’, J. Sci. Comput. 1 (1985) no. 3, 261–270.Google Scholar
Lazard, D., ‘Solving zero-dimensional algebraic systems’, J. Sci. Comput. 13 (1992) no. 2, 117–132.Google Scholar
Lubicz, D. and Robert, D., ‘Efficient pairing computation with theta functions’, Algorithmic number theory , Lecture Notes in Computer Science 6197 (Springer, Berlin, 2010) 251–269, doi:10.1007/978-3-642-14518-6_21.Google Scholar
Lubicz, D. and Robert, D., ‘Computing isogenies between abelian varieties’, Compos. Math. 148 (2012) no. 5, 1483–1515.Google Scholar
Lubicz, D. and Robert, D., ‘A generalisation of Miller’s algorithm and applications to pairing computations on abelian varieties’, J. Symbolic Comput. 67 (2015) 68–92, doi:10.1016/j.jsc.2014.08.001.Google Scholar
Mumford, D., ‘On the equations defining abelian varieties, I’, Invent. Math. 1 (1966) 287–354.Google Scholar
Mumford, D., Tata lectures on theta I , Progress in Mathematics 28 (Birkhäuser, Boston, 1983) , with the assistance of C. Musili, M. Nori, E. Previato and M. Stillman.Google Scholar
Schoof, R., ‘Elliptic curves over finite fields and the computation of square roots mod p ’, Math. Comput. 44 (1985) no. 170, 483–494.Google Scholar
Schoof, R., ‘Counting points on elliptic curves over finite fields’, J. Théor. Nombres Bordeaux 7 (1995) no. 1, 219–254.Google Scholar
Serre, J.-P., ‘Lettre à M. Tsfasman’, Astérisque 11 (1991) no. 198–200, 351–353.Google Scholar
Sutherland, A. V., ‘Computing Hilbert class polynomials with the Chinese remainder theorem’, Math. Comput. 80 (2011) no. 273, 501–538.Google Scholar