Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-18T02:10:24.742Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic moduli for unfoldings of germs of generic analytic diffeomorphisms with a codimension 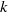$k$ parabolic point

Published online by Cambridge University Press:  28 June 2013

C. ROUSSEAU
C. ROUSSEAU*
Affiliation:
DMS and CRM, Université de Montréal, C.P. 6128, succ. Centre-ville, Montréal, Quebec, H3C 3J7, Canada email rousseac@dms.umontreal.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we provide a complete modulus of analytic classification for germs of generic analytic families of diffeomorphisms which unfold a parabolic fixed point of codimension 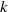$k$. We start by showing that a generic family can be ‘prepared’, i.e. brought to a prenormal form 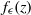${f}_{\epsilon } (z)$ in which the multi-parameter $\epsilon $ is almost canonical (up to an action of 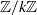$ \mathbb{Z} / k \mathbb{Z} $). As in the codimension one case treated in P. Mardešić, R. Roussarie and C. Rousseau [Modulus of analytic classification for unfoldings of generic parabolic diffeomorphisms. Mosc. Math. J. 4 (2004), 455–498], we show that the Ecalle–Voronin modulus can be unfolded to give a complete modulus for such germs. For this purpose, we define unfolded sectors in $z$-space that constitute natural domains on which the map 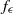${f}_{\epsilon } $ can be brought to normal form in an almost unique way. The comparison of these normalizing changes of coordinates on the different sectors forms the analytic part of the modulus. This construction is performed on sectors in the multi-parameter space $\epsilon $ such that the closure of their union provides a neighborhood of the origin in parameter space.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 1 , February 2015 , pp. 274 - 292
Creative Commons
Creative Common License - CCCreative Common License - BYCreative Common License - NCCreative Common License - SA
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution-NonCommercial-ShareAlike licence . The written permission of Cambridge University Press must be obtained for commercial re-use.
Copyright
© Cambridge University Press, 2013. The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution-NonCommercial-ShareAlike licence <http://creativecommons.org/licenses/by-nc-sa/3.0/>. The written permission of Cambridge University Press must be obtained for commercial re-use.

References

Christopher, C. and Rousseau, C.. The moduli space of germs of generic families of analytic diffeomorphisms unfolding a parabolic fixed point. Preprint, 2008, arXiv:0809.2167. Int. Math. Res. Not. to appear.CrossRefGoogle Scholar
Douady, A. and Sentenac, P.. Champs de vecteurs polynomiaux sur $ \mathbb{C} $. Preprint, 2005.Google Scholar
Glutsyuk, A. A.. Confluence of singular points and nonlinear Stokes phenomenon. Trans. Moscow Math. Soc. 62 (2001), 49–95.Google Scholar
Ilyashenko (Ed.), Y.. Nonlinear Stokes phenomena. Nonlinear Stokes Phenomena (Advances in Soviet Mathematics, 14). American Mathematical Society, Providence, RI, 1993, pp. 1–55.CrossRefGoogle Scholar
Kostov, V.. Versal deformations of differential forms of degree $\alpha $ on the line. Funct. Anal. Appl. 18 (1984), 335–337.CrossRefGoogle Scholar
Lambert, C. and Rousseau, C.. Complete system of analytic invariants for unfolded differential linear systems with an irregular singularity of Poincaré rank one. Mosc. Math. J. 12 (2012), 77–138.CrossRefGoogle Scholar
Mardešić, P., Roussarie, R. and Rousseau, C.. Modulus of analytic classification for unfoldings of generic parabolic diffeomorphisms. Mosc. Math. J. 4 (2004), 455–498.CrossRefGoogle Scholar
Martinet, J.. Remarques sur la bifurcation nœud-col dans le domaine complexe. Astérisque 150–151 (1987), 131–149.Google Scholar
Oudkerk, R.. The parabolic implosion for ${f}_{0} (z)= z+ {z}^{\nu + 1} + O({z}^{\nu + 2} )$. PhD Thesis, University of Warwick, 1999.Google Scholar
Rousseau, C.. Addendum to modulus of analytic classification for unfoldings of generic parabolic diffeomorphisms. Mosc. Math. J. 4 (2004), 499–502.Google Scholar
Rousseau, C.. Modulus of orbital analytic classification for a family unfolding a saddle-node. Mosc. Math. J. 5 (2005), 245–268.Google Scholar
Rousseau, C.. The root extraction problem. J. Differential Equations 234 (2007), 110–141.Google Scholar
Rousseau, C.. The moduli space of germs of generic families of analytic diffeomorphisms unfolding of a codimension one resonant diffeomorphism or resonant saddle. J. Differential Equations 248 (2010), 1794–1825.Google Scholar
Rousseau, C.. The modulus of unfoldings of cusps in conformal geometry. J. Differential Equations 252 (2012), 1562–1588.CrossRefGoogle Scholar
Rousseau, C. and Christopher, C.. Modulus of analytic classification for the generic unfolding of a codimension one resonant diffeomorphism or resonant saddle. Ann. Inst. Fourier (Grenoble) 57 (2007), 301–360.Google Scholar
Rousseau, C. and Teyssier, L.. Analytical moduli for unfoldings of saddle-node vector-fields. Mosc. Math. J. 8 (2008), 547–616.CrossRefGoogle Scholar
Shishikura, M.. Bifurcations of parabolic fixed points. The Mandelbrot Set, Theme and Variations (London Mathematical Society Lecture Note Series, 274). Ed. Lei, Tan. Cambridge University Press, Cambridge, 2000, pp. 325–363.CrossRefGoogle Scholar