Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-19T17:17:10.334Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular values of multiple eta-quotients for ramified primes

Part of: Abelian varieties and schemes Arithmetic algebraic geometry Computational number theory

Published online by Cambridge University Press:  07 November 2013

Andreas Enge  and
Reinhard Schertz
Andreas Enge
Affiliation:
INRIA, LFANTCNRS, IMB, UMR 5251 Université de Bordeaux, IMB33400 Talence France email andreas.enge@inria.fr
Reinhard Schertz
Affiliation:
Universität Augsburg Germany email schertz@math.uni-augsburg.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We determine the conditions under which singular values of multiple 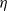$\eta $-quotients of square-free level, not necessarily prime to six, yield class invariants; that is, algebraic numbers in ring class fields of imaginary-quadratic number fields. We show that the singular values lie in subfields of the ring class fields of index 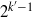${2}^{{k}^{\prime } - 1} $ when 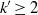${k}^{\prime } \geq 2$ primes dividing the level are ramified in the imaginary-quadratic field, which leads to faster computations of elliptic curves with prescribed complex multiplication. The result is generalised to singular values of modular functions on 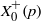${ X}_{0}^{+ } (p)$ for 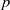$p$ prime and ramified.

MSC classification

Secondary: 14K22: Complex multiplication 11G15: Complex multiplication and moduli of abelian varieties 11Y40: Algebraic number theory computations
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 16 , October 2013 , pp. 407 - 418
Copyright
© The Author(s) 2013 

References

Belabas, K. et al. , PARI/GP. Bordeaux, Version 2.5.3, 2012, http://pari.math.u-bordeaux.fr/.Google Scholar
Elkies, N. D., ‘Elliptic and modular curves over finite fields and related computational issues’, Computational perspectives on number theory: proceedings of a conference in honor of A. O. L. Atkin, Studies in Advanced Mathematics 7 (eds Buell, D. A. and Teitelbaum, J. T.; American Mathematical Society, 1998) 21–76.Google Scholar
Enge, A., ‘Computing modular polynomials in quasi-linear time’, Math. Comp. 78 (2009) no. 267, 1809–1824.CrossRefGoogle Scholar
Enge, A. and Morain, F., Generalised Weber functions. Technical Report 385608, HAL-INRIA, 2009, http://hal.inria.fr/inria-00385608.Google Scholar
Enge, A. and Morain, F., ‘Fast decomposition of polynomials with known Galois group’, Applied algebra, algebraic algorithms and error-correcting codes — AAECC-15, Lecture Notes in Computer Science 2643 (eds Fossorier, M., Høholdt, T. and Poli, A.; Springer, Berlin, 2003) 254–264.Google Scholar
Enge, A. and Schertz, R., ‘Constructing elliptic curves over finite fields using double eta-quotients’, J. Théor. Nombres Bordeaux 16 (2004) 555–568.CrossRefGoogle Scholar
Enge, A. and Schertz, R., ‘Modular curves of composite level’, Acta Arith. 118 (2005) no. 2, 129–141.CrossRefGoogle Scholar
Enge, A. and Sutherland, A. V., ‘Class invariants by the CRT method’, Algorithmic number theory — ANTS-IX, Lecture Notes in Computer Science 6197 (eds Hanrot, G., Morain, F. and Thomé, E.; Springer, Berlin, 2010) 142–156.CrossRefGoogle Scholar
Hanrot, G. and Morain, F., ‘Solvability by radicals from an algorithmic point of view’, ISSAC 2001 — Proceedings of the 2001 International Symposium on Symbolic and Algebraic Computation (ed. Mourrain, B.; Association for Computing Machinery, New York, 2001) 175–182.CrossRefGoogle Scholar
Morain, F., ‘Calcul du nombre de points sur une courbe elliptique dans un corps fini: aspects algorithmiques’, J. Théor. Nombres Bordeaux 7 (1995) no. 1, 111–138.CrossRefGoogle Scholar
Morain, F., ‘Advances in the CM method for elliptic curves’, Slides of Fields Cryptography Retrospective Meeting, May 11–15, 2009, http://www.lix.polytechnique.fr/~morain/Exposes/fields09.pdf.Google Scholar
Schertz, R., ‘Weber’s class invariants revisited’, J. Théor. Nombres Bordeaux 14 (2002) no. 1, 325–343.CrossRefGoogle Scholar
Schertz, R., Complex multiplication (Cambridge University Press, 2010).CrossRefGoogle Scholar