Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Frijters, Stefan
Günther, Florian
and
Harting, Jens
2012.
Effects of nanoparticles and surfactant on droplets in shear flow.
Soft Matter,
Vol. 8,
Issue. 24,
p.
6542.
Huang, Wei-Xi
Chang, Cheong Bong
and
Sung, Hyung Jin
2012.
Three-dimensional simulation of elastic capsules in shear flow by the penalty immersed boundary method.
Journal of Computational Physics,
Vol. 231,
Issue. 8,
p.
3340.
Amini, Hamed
Sollier, Elodie
Weaver, Westbrook M.
and
Di Carlo, Dino
2012.
Intrinsic particle-induced lateral transport in microchannels.
Proceedings of the National Academy of Sciences,
Vol. 109,
Issue. 29,
p.
11593.
Lanauze, Javier A.
Walker, Lynn M.
and
Khair, Aditya S.
2013.
The influence of inertia and charge relaxation on electrohydrodynamic drop deformation.
Physics of Fluids,
Vol. 25,
Issue. 11,
Mukherjee, Swarnajay
and
Sarkar, Kausik
2013.
Effects of matrix viscoelasticity on the lateral migration of a deformable drop in a wall-bounded shear.
Journal of Fluid Mechanics,
Vol. 727,
Issue. ,
p.
318.
Farokhirad, Samaneh
Lee, Taehun
and
Morris, Jeffrey F.
2013.
Effects of Inertia and Viscosity on Single Droplet Deformation in Confined Shear Flow.
Communications in Computational Physics,
Vol. 13,
Issue. 3,
p.
706.
Pan, Dingyi
Phan-Thien, Nhan
and
Khoo, Boo Cheong
2014.
Dissipative particle dynamics simulation of droplet suspension in shear flow at low Capillary number.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 212,
Issue. ,
p.
63.
Singh, Rajesh Kumar
Li, Xiaoyi
and
Sarkar, Kausik
2014.
Lateral migration of a capsule in plane shear near a wall.
Journal of Fluid Mechanics,
Vol. 739,
Issue. ,
p.
421.
Horwitz, J.A.K.
Kumar, P.
and
Vanka, S.P.
2014.
Three-dimensional deformation of a spherical droplet in a square duct flow at moderate reynolds numbers.
International Journal of Multiphase Flow,
Vol. 67,
Issue. ,
p.
10.
Wang, Jingtao
Jing, Hefeng
and
Wang, Yan
2015.
Possible effects of complex internal structures on the apparent viscosity of multiple emulsions.
Chemical Engineering Science,
Vol. 135,
Issue. ,
p.
381.
Haddadi, Hamed
and
Morris, Jeffrey F.
2015.
Topology of pair-sphere trajectories in finite inertia suspension shear flow and its effects on microstructure and rheology.
Physics of Fluids,
Vol. 27,
Issue. 4,
Singh, Rajesh Kumar
and
Sarkar, Kausik
2015.
Hydrodynamic interactions between pairs of capsules and drops in a simple shear: Effects of viscosity ratio and heterogeneous collision.
Physical Review E,
Vol. 92,
Issue. 6,
Srivastava, Priyesh
Malipeddi, Abhilash Reddy
and
Sarkar, Kausik
2016.
Steady shear rheology of a viscous emulsion in the presence of finite inertia at moderate volume fractions: sign reversal of normal stress differences.
Journal of Fluid Mechanics,
Vol. 805,
Issue. ,
p.
494.
Haddadi, Hamed
Shojaei-Zadeh, Shahab
and
Morris, Jeffrey F.
2016.
Lattice-Boltzmann simulation of inertial particle-laden flow around an obstacle.
Physical Review Fluids,
Vol. 1,
Issue. 2,
Zhang, Yuzhou
Xu, Junbo
and
He, Xianfeng
2018.
Effect of surfactants on the deformation of single droplet in shear flow studied by dissipative particle dynamics.
Molecular Physics,
Vol. 116,
Issue. 14,
p.
1851.
Krishnamurthy, Deepak
and
Subramanian, Ganesh
2018.
Heat or mass transport from drops in shearing flows. Part 2. Inertial effects on transport.
Journal of Fluid Mechanics,
Vol. 850,
Issue. ,
p.
484.
Mwasame, Paul M.
Wagner, Norman J.
and
Beris, Antony N.
2019.
Micro-Inertia Effects in Material Flow.
Journal of Non-Equilibrium Thermodynamics,
Vol. 44,
Issue. 3,
p.
235.
Razavi Bazaz, Sajad
Mashhadian, Ali
Ehsani, Abbas
Saha, Suvash Chandra
Krüger, Timm
and
Ebrahimi Warkiani, Majid
2020.
Computational inertial microfluidics: a review.
Lab on a Chip,
Vol. 20,
Issue. 6,
p.
1023.
Jing, Wenyang
and
Han, Hee-Sun
2022.
Inertial Self-Assembly Dynamics of Interacting Droplet Ensembles in Microfluidic Flows.
Analytical Chemistry,
Vol. 94,
Issue. 9,
p.
3978.
Mukherjee, Swarnajay
Tarafder, Anik
Malipeddi, Abhilash Reddy
and
Sarkar, Kausik
2022.
Shear-induced migration of a viscous drop in a viscoelastic liquid near a wall at high viscosity ratio: Reverse migration.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 301,
Issue. ,
p.
104751.
 (the direction of maximum extension), critically affecting the interfacial stresses due to the drop. It changes the sign of first and second normal interfacial stress differences (and thereby these components of the effective stresses of an emulsion of such drops). Increasing viscosity ratio orients the drop towards the flow axis, which increases the critical Reynolds number above which the drop inclination reaches more than
(the direction of maximum extension), critically affecting the interfacial stresses due to the drop. It changes the sign of first and second normal interfacial stress differences (and thereby these components of the effective stresses of an emulsion of such drops). Increasing viscosity ratio orients the drop towards the flow axis, which increases the critical Reynolds number above which the drop inclination reaches more than 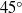 .
.



