Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-24T18:41:45.463Z Has data issue: false hasContentIssue false
  • English
  • Français

Gevrey spaces and their intersections

Part of: Lie groups

Published online by Cambridge University Press:  09 April 2009

A. F. M. Ter Elst
A. F. M. Ter Elst
Affiliation:
Department of MathematicsEindhoven University of TechnologyP.O. Box 513 5600 MB Eindhoven, The Netherlands
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For unbounded operators A1, …, Ad, Gevrey spaces Sλ1, …, λd (A1, …, Ad) of order (λ1, …, λd) are introduced, where the orders λ1, …, λd need not be equal. These extend the notion of Gevrey space defined by Goodman and Wallach where λ1 = … = λd. Several mild conditions on the operators A1, … Ad and the orders λ1, …, λd are presented such that the equality 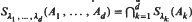is valid. Examples are included.

MSC classification

Secondary: 22E45: Representations of Lie and linear algebraic groups over real fields
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 54 , Issue 2 , April 1993 , pp. 263 - 286
Copyright
Copyright © Australian Mathematical Society 1993

References

[1]Browder, F. E., ‘Real analytic functions on product spaces and separate analyticity’, Canadian J. Math 13 (1961), 650–656.CrossRefGoogle Scholar
[2]van Eijndhoven, S. J. L., ‘Functional analytic characterizations of the Gelfand-Shiov spaces ’, Proc. Kon. Nederl. Akad. Wetensch. A 90 (1987), 133–144.CrossRefGoogle Scholar
[3]Fans, W. G., Self adfoint operators, Lecture Notes in Math. 433 (Springer, Berlin, 1975).Google Scholar
[4]Flato, M., and Simon, J., ‘Separate and joint analyticity in Lie groups representations’, J. Funct. Anal. 13 (1973), 268–276.CrossRefGoogle Scholar
[5]Gelfand, I. M., and Shiov, G. E., Generalized functions, vol. 2 (Academic Press, New York, 1968).Google Scholar
[6]Gevrey, M., ‘Sur la nature analytique des solutions des équations aux dérivées partielles’, Ann. Sci. École Norm. Sup. 35 (1918), 129–190.CrossRefGoogle Scholar
[7]Goodman, R., ‘Analytic and entire vectors for representations of Lie groups’, Trans. Amer. Math. Soc. 143 (1969), 55–76.CrossRefGoogle Scholar
[8]Goodman, R., ‘Complex Fourier analysis on a nilpotent Lie group’, Trans. Amer. Math. Soc. 160 (1971), 373–391.CrossRefGoogle Scholar
[9]Goodman, R., ‘Elliptic and subelliptic estimates for operators in an enveloping algebra’, Duke Math. J. 47 (1980), 819–833.CrossRefGoogle Scholar
[10]Goodman, R., and Waflach, N. R., ‘Whittaker vectors and conical vectors’, J. Funct. Anal. 39 (1980), 199–279.CrossRefGoogle Scholar
[11]Nelson, E., ‘Analytic vectors’, Ann. of Math. 70 (1959), 572–615.CrossRefGoogle Scholar
[12]Paley, R. E. A. C., and Wiener, N., Fourier transforms in the complex domain, Colloquium Publications 19 (Amer. Math. Soc., New York, 1934).Google Scholar
[13]Pukanszky, L., Leçons sur les représentations des groupes (Dunod, Paris, 1967).Google Scholar
[14]Taylor, M. E., Noncommutative harmonic analysis, Math. Surveys Monographs 22 (Amer. Math. Soc., Providence, 1986).CrossRefGoogle Scholar
[15]Varadarajan, V. S., Lie groups, Lie algebras, and their representations, Graduate Texts in Math. 102 (Springer, New York, 1984).CrossRefGoogle Scholar
[16]Wloka, J., Grundräume and verallgemeinerte Funktionen, Lecture Notes in Math. 82 (Springer, Berlin, 1969).CrossRefGoogle Scholar