Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kim, Henry H.
and
Yamauchi, Takuya
2018.
A Miyawaki type lift for $$\textit{GSpin}(2,10)$$ GSpin ( 2 , 10 ).
Mathematische Zeitschrift,
Vol. 288,
Issue. 1-2,
p.
415.
Kim, Henry H.
and
Yamauchi, Takuya
2019.
Non-vanishing of Miyawaki type lifts.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 89,
Issue. 2,
p.
117.
Pollack, Aaron
2020.
The Fourier expansion of modular forms on quaternionic exceptional groups.
Duke Mathematical Journal,
Vol. 169,
Issue. 7,
Li, Yingkun
Narita, Hiro-aki
and
Pitale, Ameya
2020.
An explicit construction of non-tempered cusp forms on $$O(1,8n+1)$$.
Annales mathématiques du Québec,
Vol. 44,
Issue. 2,
p.
349.
Yamana, Shunsuke
2020.
On the lifting of Hilbert cusp forms to Hilbert-Hermitian cusp forms.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 8,
p.
5395.
Katsurada, Hidenori
Kim, Henry H.
and
Yamauchi, Takuya
2022.
Period of the Ikeda type lift for the exceptional group of type $$E_{7,3}$$.
Mathematische Zeitschrift,
Vol. 302,
Issue. 1,
p.
559.
Kim, Henry H.
and
Yamauchi, Takuya
2023.
Higher level cusp forms on exceptional group of type E7.
Kyoto Journal of Mathematics,
Vol. 63,
Issue. 3,
Katsurada, Hidenori
and
Kim, Henry H.
2023.
Twisted Koecher-Maass series of the Ikeda type lift for the exceptional group of type E7,3.
Journal of Number Theory,
Vol. 248,
Issue. ,
p.
140.
Narita, Hiro-aki
Pitale, Ameya
and
Wagh, Siddhesh
2023.
An explicit lifting construction of CAP forms on O(1,5).
International Journal of Number Theory,
Vol. 19,
Issue. 06,
p.
1337.
Günaydin, Murat
and
Kidambi, Abhiram
2024.
Octonionic Magical Supergravity, Niemeier Lattices, and Exceptional & Hilbert Modular Forms.
Fortschritte der Physik,
Vol. 72,
Issue. 2,
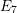 $E_{7}$
$E_{7}$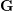 $\mathbf{G}$ be the connected reductive group of type
$\mathbf{G}$ be the connected reductive group of type 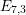 $E_{7,3}$ over
$E_{7,3}$ over  $\mathbb{Q}$ and
$\mathbb{Q}$ and 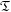 $\mathfrak{T}$ be the corresponding symmetric domain in
$\mathfrak{T}$ be the corresponding symmetric domain in 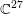 $\mathbb{C}^{27}$. Let
$\mathbb{C}^{27}$. Let 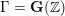 ${\rm\Gamma}=\mathbf{G}(\mathbb{Z})$ be the arithmetic subgroup defined by Baily. In this paper, for any positive integer
${\rm\Gamma}=\mathbf{G}(\mathbb{Z})$ be the arithmetic subgroup defined by Baily. In this paper, for any positive integer 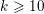 $k\geqslant 10$, we will construct a (non-zero) holomorphic cusp form on
$k\geqslant 10$, we will construct a (non-zero) holomorphic cusp form on 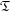 $\mathfrak{T}$ of weight
$\mathfrak{T}$ of weight 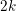 $2k$ with respect to
$2k$ with respect to 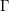 ${\rm\Gamma}$ from a Hecke cusp form in
${\rm\Gamma}$ from a Hecke cusp form in 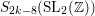 $S_{2k-8}(\text{SL}_{2}(\mathbb{Z}))$. We follow Ikeda’s idea of using Siegel’s Eisenstein series, their Fourier–Jacobi expansions, and the compatible family of Eisenstein series.
$S_{2k-8}(\text{SL}_{2}(\mathbb{Z}))$. We follow Ikeda’s idea of using Siegel’s Eisenstein series, their Fourier–Jacobi expansions, and the compatible family of Eisenstein series.



