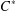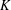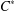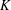Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Patterson, Quinn
Sierakowski, Adam
Sims, Aidan
and
Taylor, Jonathan
2021.
Graded K-theory and K-homology of relative Cuntz–Pimsner algebras and graph C⁎-algebras.
Journal of Mathematical Analysis and Applications,
Vol. 496,
Issue. 2,
p.
124822.