Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-17T22:54:32.263Z Has data issue: false hasContentIssue false
  • English
  • Français

Triadic resonances in precessing rapidly rotating cylinder flows

Published online by Cambridge University Press:  30 July 2015

T. Albrecht ,
H. M. Blackburn ,
J. M. Lopez ,
R. Manasseh  and
P. Meunier
T. Albrecht*
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
H. M. Blackburn
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
J. M. Lopez
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, Tempe, AZ 85287, USA
R. Manasseh
Affiliation:
Department of Mechanical and Product Design Engineering, Swinburne University of Technology, VIC 3122, Australia
P. Meunier
Affiliation:
IRPHE, CNRS, Aix–Marseille Université, 49 Rue Joliot-Curie, 13013 Marseille, France
*
†Email address for correspondence: thomas.albrecht@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations of flows in cylinders subjected to both rapid rotation and axial precession are presented and analysed in the context of a stability theory based on the triadic resonance of Kelvin modes. For a case that was chosen to provide a finely tuned resonant instability with a small nutation angle, the simulations are in good agreement with the theory and previous experiments in terms of mode shapes and dynamics, including long-time-scale regularization of the flow and recurrent collapses. Cases not tuned to the most unstable triad, but with the nutation angle still small, are also in quite good agreement with theoretical predictions, showing that the presence of viscosity makes the physics of the triadic-resonance model robust to detuning. Finally, for a case with 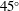$45^{\circ }$ nutation angle for which it has been suggested that resonance does not occur, the simulations show that a slowly growing triadic resonance predicted by theory is in fact observed if sufficient evolution time is allowed.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Instability: Nonlinear instability Geophysical and Geological Flows: Waves in rotating fluids
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , R1
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blackburn, H. M. & Sherwin, S. J. 2004 Formulation of a Galerkin spectral element–Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.Google Scholar
Craik, A. D. D. 1988 Wave Interactions and Fluid Flows. Cambridge University Press.Google Scholar
Fultz, D. 1959 A note on overstability and the elastoid-inertia oscillations of Kelvin, Solberg and Bjerknes. Meteorology 16, 199–208.2.0.CO;2>CrossRefGoogle Scholar
Gans, R. F. 1970 On the precession of a resonant cylinder. J. Fluid Mech. 476, 865–872.CrossRefGoogle Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Kelvin, L. 1880 Vibrations of a columnar vortex. Phil. Mag. 10, 155–168.Google Scholar
Kerswell, R. R. 1999 Secondary instabilities in rapidly rotating fluids: inertial wave breakdown. J. Fluid Mech. 382, 283–306.CrossRefGoogle Scholar
Kerswell, R. R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34, 83–113.Google Scholar
Kong, D., Cui, Z., Liao, X. & Zhang, K. 2015 On the transition from the laminar to disordered flow in a precessing spherical-like cylinder. Geophys. Astrophys. Fluid Dyn. 109, 62–83.Google Scholar
Lagrange, R., Eloy, C., Nadal, F. & Meunier, P. 2008 Instability of a fluid inside a precessing cylinder. Phys. Fluids 20, 081701.CrossRefGoogle Scholar
Lagrange, R., Meunier, P., Nadal, F. & Eloy, C. 2011 Precessional instability of a fluid cylinder. J. Fluid Mech. 666, 104–145.Google Scholar
Mahalov, A. 1993 The instability of rotating fluid columns subjected to a weak external Coriolis force. Phys. Fluids A 5, 891–900.Google Scholar
Manasseh, R. 1992 Breakdown regimes of inertia waves in a precessing cylinder. J. Fluid Mech. 243, 261–296.Google Scholar
Manasseh, R. 1994 Distortions of inertia waves in a rotating fluid cylinder forced near its fundamental mode resonance. J. Fluid Mech. 265, 345–370.CrossRefGoogle Scholar
Manasseh, R. 1996 Nonlinear behaviour of contained inertia waves. J. Fluid Mech. 315, 151–173.Google Scholar
McEwan, A. D. 1970 Inertial oscillations in a rotating fluid cylinder. J. Fluid Mech. 40, 603–640.CrossRefGoogle Scholar
Meunier, P., Eloy, C., Lagrange, R. & Nadal, F. 2008 A rotating fluid cylinder subject to weak precession. J. Fluid Mech. 599, 405–440.Google Scholar

Albrecht et al. supplementary movie

For the flow in figure 2 (b), Γ=1.62, α=1°, Po=-0.153, Re=7670, this movie shows positive (red) and negative (yellow) isosurfaces of helicity, visualised in the gimbal frame of reference, but with helicity computed after the background rotation was removed. As indicated by the vertical lines in figure 2 (b), the movie shows one cycle of the terminal low-frequency oscillation, over ≈40 cylinder rotations.

Download Albrecht et al. supplementary movie(Video)
Video 2 MB

Albrecht et al. supplementary movie

For the flow in figure 2 (b), Γ=1.62, α=1°, Po=-0.153, Re=7670, this movie shows positive (red) and negative (yellow) isosurfaces of helicity, visualised in the gimbal frame of reference, but with helicity computed after the background rotation was removed. As indicated by the vertical lines in figure 2 (b), the movie shows one cycle of the terminal low-frequency oscillation, over ≈40 cylinder rotations.

Download Albrecht et al. supplementary movie(Video)
Video 1.9 MB

Albrecht et al. supplementary movie

This shows axial vorticity for the flow represented in figure 2 (a): Γ=1.62, α=0.8°, Po=-0.153, Re=5310 after the final saturated state is reached. The flow was computed and visualised in the cylinder frame of reference. We filtered the velocity field to azimuthal wave number m=1 (a), m=5 (b), and m=6 (c). Then we extracted contours of axial vorticity at their maximum planes, i.e., one-quarter of the cylinder height for m=1 and m=5, and one-half form=6. As predicted for a triadic resonance, the forced mode rotates at -Ω1, while the parasitic modes m=5 and m=6 counter-rotate.

Download Albrecht et al. supplementary movie(Video)
Video 941.8 KB

Albrecht et al. supplementary movie

This shows axial vorticity for the flow represented in figure 2 (a): Γ=1.62, α=0.8°, Po=-0.153, Re=5310 after the final saturated state is reached. The flow was computed and visualised in the cylinder frame of reference. We filtered the velocity field to azimuthal wave number m=1 (a), m=5 (b), and m=6 (c). Then we extracted contours of axial vorticity at their maximum planes, i.e., one-quarter of the cylinder height for m=1 and m=5, and one-half form=6. As predicted for a triadic resonance, the forced mode rotates at -Ω1, while the parasitic modes m=5 and m=6 counter-rotate.

Download Albrecht et al. supplementary movie(Video)
Video 1.6 MB

Albrecht et al. supplementary movie

The same flow and equivalent data processing as for movie 2, but computed and visualised in the gimbal frame of reference, shows a steady forced mode and co-rotating parasitic modes.

Download Albrecht et al. supplementary movie(Video)
Video 1.3 MB

Albrecht et al. supplementary movie

The same flow and equivalent data processing as for movie 2, but computed and visualised in the gimbal frame of reference, shows a steady forced mode and co-rotating parasitic modes.

Download Albrecht et al. supplementary movie(Video)
Video 2.2 MB