Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-18T21:05:37.127Z Has data issue: false hasContentIssue false
  • English
  • Français

Skew products, quantitative recurrence, shrinking targets and decay of correlations

Published online by Cambridge University Press:  03 July 2014

STEFANO GALATOLO ,
JÉRÔME ROUSSEAU  and
BENOIT SAUSSOL
STEFANO GALATOLO
Affiliation:
Dipartimento di Matematica Applicata ‘U. Dini’, Universitá di Pisa, Via Buonarroti 1, Pisa, Italy email s.galatolo@ing.unipi.it
JÉRÔME ROUSSEAU
Affiliation:
Departamento de Matemática, Universidade Federal da Bahia, Av. Ademar de Barros s/n, 40170-110 Salvador, Brazil email jerome.rousseau@ufba.br
BENOIT SAUSSOL
Affiliation:
Université Européenne de Bretagne, Université de Brest, Laboratoire de Mathématiques CNRS UMR 6205, 6 avenue Victor le Gorgeu, CS93837, F-29238 Brest Cedex 3, France email benoit.saussol@univ-brest.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

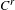We consider toral extensions of hyperbolic dynamical systems. We prove that its quantitative recurrence (also with respect to given observables) and hitting time scale behavior depend on the arithmetical properties of the extension. By this we show that those systems have a polynomial decay of correlations with respect to $C^{r}$ observables, and give estimations for its exponent, which depend on $r$ and on the arithmetical properties of the system. We also show examples of systems of this kind having no shrinking target property, and having a trivial limit distribution of return time statistics.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 6 , September 2015 , pp. 1814 - 1845
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abadi, M. and Galves, A.. Inequalities for the occurence time of rare events in mixing processes. The state of the art. Markov Process. Related Fields 7 (2001), 97–112.Google Scholar
Barreira, L.. Dimension and Recurrence in Hyperbolic Dynamics (Progress in Mathematics, 272). Birkhäuser, Basel, 2008.Google Scholar
Barreira, L. and Saussol, B.. Hausdorff dimension of measures via Poincaré recurrence. Comm. Math. Phys. 219(2) (2001), 443–463.CrossRefGoogle Scholar
Boshernitzan, M. D.. Quantitative recurrence results. Invent. Math. 113 (1993), 617–631.CrossRefGoogle Scholar
Boshernitzan, M. D. and Chaika, J.. Diophantine properties of IETs and general systems: quantitative proximality and connectivity. Invent. Math 192(2) (2013), 375–412.CrossRefGoogle Scholar
Cassels, J. W. S.. An Introduction to Diophantine Approximation (Cambridge Tracts in Mathematics and Mathematical Physics, 45). Cambridge University Press, Cambridge, 1957.Google Scholar
Chazottes, J.-R., Collet, P. and Schmitt, B.. Statistical consequences of the Devroye inequality for processes Applications to a class of non-uniformly hyperbolic dynamical systems. Nonlinearity 18(5) (2005).Google Scholar
Dolgopyat, D.. On mixing properties of compact group extensions of hyperbolic systems. Israel J. Math. 130 (2002), 157–205.CrossRefGoogle Scholar
Fayad, B.. Analytic mixing reparametrizations of irratonal flows. Ergod. Th. & Dynam. Sys. 22(2) (2002), 437–468.Google Scholar
Fayad, B.. Mixing in the absence of the shrinking target property. Bull. Lond. Math. Soc. 38(5) (2006), 829–838.CrossRefGoogle Scholar
Freitas, A. C. M., Freitas, J. M. and Todd, M.. Hitting time statistics and extreme value theory. Probab. Theory Related Fields 147(3–4) (2010), 675–710.CrossRefGoogle Scholar
Galatolo, S.. Dimension and hitting time in rapidly mixing systems. Math. Res. Lett. 14(5) (2007), 797–805.CrossRefGoogle Scholar
Galatolo, S.. Dimension via waiting time and recurrence. Math. Res. Lett. 12(3) (2005), 377–386.CrossRefGoogle Scholar
Galatolo, S.. Hitting time and dimension in axiom A systems, generic interval exchanges and an application to Birkoff sums. J. Stat. Phys. 123 (2006), 111–124.CrossRefGoogle Scholar
Galatolo, S.. Hitting time in regular sets and logarithm law for rapidly mixing dynamical systems. Proc. Amer. Math. Soc. 138(7) (2010), 2477–2487.CrossRefGoogle Scholar
Galatolo, S. and Kim, D. H.. The dynamical Borel–Cantelli lemma and the waiting time problems. Indag. Math. (N.S.) 18(3) (2007), 421–434.CrossRefGoogle Scholar
Galatolo, S. and Nisoli, I.. Shrinking targets in fast mixing flows and the geodesic flow on negatively curved manifolds. Nonlinearity 24 (2011), 3099–3113.CrossRefGoogle Scholar
Galatolo, S. and Pacifico, M. J.. Lorenz like flows: exponential decay of correlations for the Poincaré map, logarithm law, quantitative recurrence. Ergod. Th. & Dynam. Sys. 30(6) (2010), 1703–1737.CrossRefGoogle Scholar
Galatolo, S. and Peterlongo, P.. Long hitting time, slow decay of correlations and arithmetical properties. Discrete Contin. Dyn. Syst. 27(1) (2010), 185–204.CrossRefGoogle Scholar
Gouezel, S.. Local limit theorem for nonuniformly partially hyperbolic skew-products and Farey sequences. Duke Math. J. 147 (2009), 192–284.CrossRefGoogle Scholar
Hennion, H. and Hervé, L.. Limit Theorems for Markov Chains and Stochastic Properties of Dynamical Systems by Quasi-Compactness (Lecture Notes in Mathematics, 1766). Springer, Berlin, 2001.CrossRefGoogle Scholar
Hill, R. and Velani, S.. The ergodic theory of shrinking targets. Invent. Math. 119 (1995), 175–198.CrossRefGoogle Scholar
Kim, D. H. and Marmi, S.. The recurrence time for interval exchange maps. Nonlinearity 21 (2008), 2201–2210.CrossRefGoogle Scholar
Kim, D. H. and Seo, B. K.. The waiting time for irrational rotations. Nonlinearity 16 (2003), 1861–1868.CrossRefGoogle Scholar
Kleinbock, D. Y. and Margulis, G. A.. Logarithm laws for flows on homogeneous spaces. Invent. Math. 138 (1999), 451–494.CrossRefGoogle Scholar
Kuipers, L. and Niederreiter, H.. Uniform distribution of sequences. Pure and Applied Mathematics. Wiley-Interscience, 1974.Google Scholar
Marwan, N., Romano, M. C., Thiel, M. and Kurths, J.. Recurrence plots for the analysis of complex systems. Phys. Rep. 438 (2007), 237–329.CrossRefGoogle Scholar
Masur, H.. Logarithmic law for geodesics in moduli space. Mapping Class Groups and Moduli Spaces of Riemann Surfaces (Gottingen, 1991/Seattle, WA, 1991) (Contemporary Mathematics, 150). American Mathematical Society, Providence, RI, 1993, pp. 229–245.CrossRefGoogle Scholar
Ornstein, D. and Weiss, B.. Entropy and data compression schemes. IEEE Trans. Inform. Theory 39 (1993), 78–83.CrossRefGoogle Scholar
Philipp, W.. Some metrical theorems in number theory. Pacific J. Math. 20 (1967), 109–127.CrossRefGoogle Scholar
Rousseau, J.. Recurrence rates for observations of flows. Ergod. Th. & Dynam. Sys. 32 (2012), 1727–1751.CrossRefGoogle Scholar
Rousseau, J. and Saussol, B.. Poincaré recurrence for observations. Trans. Amer. Math. Soc. 362 (2010), 5845–5859.CrossRefGoogle Scholar
Saussol, B.. An introduction to quantitative Poincaré recurrence in dynamical systems. Rev. Math. Phys. 21(8) (2009), 949–979.CrossRefGoogle Scholar
Saussol, B.. Recurrence rate in rapidly mixing dynamical systems. Discrete Contin. Dyn. Syst. 15(1) (2006), 259–267.CrossRefGoogle Scholar
Su, F. E.. Convergence of random walks on the circle generated by an irrational rotation. Trans. Amer. Math. Soc. 350 (1998), 3717–3741.CrossRefGoogle Scholar
Sullivan, D.. Disjoint spheres, approximation by imaginary quadratic numbers, and the logarithm law for geodesics. Acta Math. 149 (1982), 215–237.CrossRefGoogle Scholar