Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-23T22:37:00.394Z Has data issue: false hasContentIssue false
  • English
  • Français

Loci of complex polynomials, part II: polar derivatives

Published online by Cambridge University Press:  19 June 2015

BLAGOVEST SENDOV  and
HRISTO SENDOV
BLAGOVEST SENDOV
Affiliation:
Bulgarian Academy of Sciences, Institute of Information and Communication Technologies, Acad. G. Bonchev Str., bl. 25A, 1113 Sofia, Bulgaria. e-mail: acad@sendov.com
HRISTO SENDOV
Affiliation:
Department of Statistical and Actuarial Sciences, Western University, 1151 Richmond Str., London, ON, N6A 5B7, Canada. e-mail: hssendov@stats.uwo.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

For every complex polynomial p(z), closed point sets are defined, called loci of p(z). A closed set Ω ⊆ 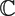${\mathbb C}$* is a locus of p(z) if it contains a zero of any of its apolar polynomials and is the smallest such set with respect to inclusion. Using the notion locus, some classical theorems in the geometry of polynomials can be refined. We show that each locus is a Lebesgue measurable set and investigate its intriguing connections with the higher-order polar derivatives of p.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 159 , Issue 2 , September 2015 , pp. 253 - 273
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Borwein, J. M. and Bailey, D. H. Mathematics by Experiment: Plausible Reasoning in the 21st Century (A.K. Peters, Ltd., 2004).Google Scholar
[2] Grace, J. H. The zeros of a polynomial. Proc. Camb. Phil. Soc. 11 (1902), 352–357.Google Scholar
[3] Rahman, Q. I. and Schmeisser, G. Analytic Theory of Polynomials (Oxford University Press Inc., New York, 2002).Google Scholar
[4] Roy, R. Binomial identities and hypergeometric series. Amer. Math. Monthly 1 (94) (1987), 36–46.Google Scholar
[5] Sendov, Bl. and Sendov, H. Loci of complex polynomials, part I. Trans. Amer. Math. Soc. submitted 2012.Google Scholar
[6] Szegő, G. Bemerkungen zu einem Satz von J. H. Grace uber die Wurzeln algebraischer Gleichungen Math. Z. 13 (1922), 28–55.Google Scholar
[7] Wagner, D. G. Multivariate stable polynomials: theory and applications Bull. Amer. Math. Soc. 48 (1) (2011), 53–84.Google Scholar