Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-24T01:30:47.835Z Has data issue: false hasContentIssue false
  • English
  • Français

Query Complexity of Sampling and Small Geometric Partitions

Published online by Cambridge University Press:  21 October 2014

NAVIN GOYAL ,
LUIS RADEMACHER  and
SANTOSH VEMPALA
NAVIN GOYAL
Affiliation:
Microsoft Research India, Vigyan, 9 Lavelle Road, Bangalore 560001, India (e-mail: navingo@microsoft.com)
LUIS RADEMACHER
Affiliation:
Computer Science and Engineering, Ohio State University, Dreese Labs 495 2015 Neil Avenue, Columbus, OH 43210, USA (e-mail: lrademac@cse.ohio-state.edu)
SANTOSH VEMPALA
Affiliation:
College of Computing, Georgia Institute of Technology, 801 Atlantic Drive, Atlanta, GA 30332, USA (e-mail: vempala@cc.gatech.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the following problem.

Discrete partitioning problem (DPP). Let 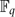$\mathbb{F}_q$Pn denote the n-dimensional finite projective space over 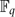$\mathbb{F}_q$. For positive integer k ⩽ n, let {Ai}i = 1N be a partition of (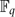$\mathbb{F}_q$Pn)k such that:

  1. (1) for all i ⩽ N, Ai = ∏j=1kAji (partition into product sets),

  2. (2) for all i ⩽ N, there is a (k − 1)-dimensional subspace Li ⊆ 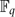$\mathbb{F}_q$Pn such that Ai ⊆ (Li)k.

What is the minimum value of N as a function of q, n, k? We will be mainly interested in the case k = n.

DPP arises in an approach that we propose for proving lower bounds for the query complexity of generating random points from convex bodies. It is also related to other partitioning problems in combinatorics and complexity theory. We conjecture an asymptotically optimal partition for DPP and show that it is optimal in two cases: when the dimension is low (k = n = 2) and when the factors of the parts are structured, namely factors of a part are close to being a subspace. These structured partitions arise naturally as partitions induced by query algorithms. Our problem does not seem to be directly amenable to previous techniques for partitioning lower bounds such as rank arguments, although rank arguments do lie at the core of our techniques.

Keywords

Primary 68Q17Secondary 68R0551E20
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 24 , Issue 5 , September 2015 , pp. 733 - 753
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Alon, N. (1986) Decomposition of the complete r-graph into complete r-partite r-graphs. Graphs Combin. 2 95–100.CrossRefGoogle Scholar
[2] Alon, N., Bohman, T., Holzman, R. and Kleitman, D. J. (2002) On partitions of discrete boxes. Discrete Math. 257 255–258.CrossRefGoogle Scholar
[3] Babai, L. and Frankl, P. (1992) Linear Algebra Methods in Combinatorics, Department of Computer Science, University of Chicago.Google Scholar
[4] Beame, P., Pitassi, T., Segerlind, N. and Wigderson, A. (2006) A strong direct product theorem for corruption and the multiparty communication complexity of disjointness. Comput. Complex. 15 391–432.CrossRefGoogle Scholar
[5] Bertsimas, D. and Vempala, S. (2004) Solving convex programs by random walks. J. Assoc. Comput. Mach. 51 540–556.CrossRefGoogle Scholar
[6] Braun, G., Jain, R., Lee, T. and Pokutta, S. (2013) Information-theoretic approximations of the nonnegative rank. Electronic Colloquium on Computational Complexity: ECCC 20 158.Google Scholar
[7] Chakrabarti, A. and Regev, O. (2012) An optimal lower bound on the communication complexity of gap-Hamming-distance. SIAM J. Comput. 41 1299–1317.CrossRefGoogle Scholar
[8] Cioaba, S. M., Kündgen, A. and Verstraëte, J. (2009) On decompositions of complete hypergraphs. J. Combin. Theory Ser. A 116 1232–1234.CrossRefGoogle Scholar
[9] Dvir, Z. (2009) On the size of Kakeya sets in finite fields. J. Amer. Math. Soc. 22 1093–1097.CrossRefGoogle Scholar
[10] Faure, C.-A. and Frölicher, A. (2000) Modern Projective Geometry, Kluwer.CrossRefGoogle Scholar
[11] Fawzi, H. and Parrilo, P. A. (2012) New lower bounds on nonnegative rank using conic programming, http://arxiv.org/abs/1210.6970.Google Scholar
[12] Graham, R. and Pollak, H. (1971) On the addressing problem for loop switching. Bell Syst. Tech. J. 50 2495–2519.CrossRefGoogle Scholar
[13] Grötschel, M., Lovász, L. and Schrijver, A. (1988) Geometric Algorithms and Combinatorial Optimization, Springer.CrossRefGoogle Scholar
[14] Jain, R. and Klauck, H. (2010) The partition bound for classical communication complexity and query complexity. In IEEE Conference on Computational Complexity, pp. 247–258.CrossRefGoogle Scholar
[15] Kushilevitz, E. and Nisan, N. (1996) Communication Complexity, Cambridge University Press.CrossRefGoogle Scholar
[16] Lovász, L. and Vempala, S. (2006) Fast algorithms for logconcave functions: Sampling, rounding, integration and optimization. In IEEE Symposium on Foundations of Computer Science, pp. 57–68.CrossRefGoogle Scholar
[17] Motwani, R. and Raghavan, P. (1995) Randomized Algorithms, Cambridge University Press.CrossRefGoogle Scholar
[18] Rademacher, L. and Vempala, S. (2008) Dispersion of mass and the complexity of randomized geometric algorithms. Adv. Math. 219 1037–1069.CrossRefGoogle Scholar
[19] Razborov, A. A. (1990) Applications of matrix methods to the theory of lower bounds in computational complexity. Combinatorica 10 81–93.CrossRefGoogle Scholar