Hostname: page-component-8448b6f56d-sxzjt Total loading time: 0 Render date: 2024-04-25T03:43:12.197Z Has data issue: false hasContentIssue false
  • English
  • Français

Quadratic stochastic operators and zero-sum game dynamics

Published online by Cambridge University Press:  20 June 2014

NASIR N. GANIKHODJAEV ,
RASUL N. GANIKHODJAEV  and
U. U. JAMILOV
NASIR N. GANIKHODJAEV
Affiliation:
Department of Computational and Theoretical Sciences, Faculty of Science, IIUM, 25200 Kuantan, Malaysia email nasirgani@hotmail.com
RASUL N. GANIKHODJAEV
Affiliation:
Department of Algebra and Functional Analysis, Faculty of Mathematics, National University of Uzbekistan, 100095 Tashkent, Uzbekistan email rasulgani@hotmail.com
U. U. JAMILOV
Affiliation:
Institute of Mathematics at the National University of Uzbekistan, 29, Do’rmon Yo’li str., 100125 Tashkent, Uzbekistan email jamilovu@yandex.ru
Get access Rights & Permissions [Opens in a new window]

Abstract

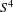In this paper we consider the set of all extremal Volterra quadratic stochastic operators defined on a unit simplex $S^{4}$ and show that such operators can be reinterpreted in terms of zero-sum games. We show that an extremal Volterra operator is non-ergodic and an appropriate zero-sum game is a rock-paper-scissors game if either the Volterra operator is a uniform operator or for a non-uniform Volterra operator $V$ there exists a subset 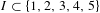$I\subset \{1,2,3,4,5\}$ with $|I|\leq 2$ such that $\sum _{i\in I}(V^{n}\mathbf{x})_{i}\rightarrow 0,$ and the restriction of $V$ on an invariant face 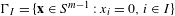${\rm\Gamma}_{I}=\{\mathbf{x}\in S^{m-1}:x_{i}=0,i\in I\}$ is a uniform Volterra operator.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 5 , August 2015 , pp. 1443 - 1473
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E. and Losert, V.. Evolutionary dynamics of zero-sum games. J. Math. Biol. 20 (1984), 231–258.CrossRefGoogle ScholarPubMed
Akin, E. The General Topology of Dynamical Systems (Graduate Studies in Mathematics, 1). American Mathematical Society, Providence, RI, 1993.Google Scholar
Bernstein, S. N.. The solution of a mathematical problem related to the theory of heredity. Uchn. Zapiski. NI Kaf. Ukr. Otd. Mat.(1) (1924), 83–115 (in Russian).Google Scholar
Devaney, R. L.. An Introduction to Chaotic Dynamical Systems (Studies in Nonlinearity). Westview Press, Boulder, CO, 2003.Google Scholar
Ganikhodjaev, N. N. and Zanin, D. V.. On a necessary condition for the ergodicity of quadratic operators defined on the two-dimensional simplex. Russian Math. Surveys 59(3) (2004), 571–572.CrossRefGoogle Scholar
Ganikhodjaev, N. N. and Zanin, D. V.. Ergodic Volterra quadratic maps of the simplex. Preprint arXiv:1205.3841 (in Russian).Google Scholar
Ganikhodjaev, N. N., Jamilov, U. U. and Mukhitdinov, R. T.. On non-ergodic transformations on S 3. J. Phys.: Conf. Ser. 435 (2013), 012005.Google Scholar
Ganikhodzhaev, R. N.. Quadratic stochastic operators, Lyapunov function and tournaments. Acad. Sci. Sb. Math. 76(2) (1993), 489–506.CrossRefGoogle Scholar
Ganikhodzhaev, R. N.. A chart of fixed points and Lyapunov functions for a class of discrete dynamical systems. Math. Notes 56(5–6) (1994), 1125–1131.CrossRefGoogle Scholar
Ganikhodzhaev, R. N. and Eshmamatova, D. B.. Quadratic automorphisms of a simplex and the asymptotic behavior of their trajectories. Vladikavkaz. Mat. Zh. 8(2) (2006), 12–28 (in Russian).Google Scholar
Ganikhodzhaev, R. N., Mukhamedov, F. M. and Rozikov, U. A.. Quadratic stochastic operators: Results and open problems. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 14(2) (2011), 279–335.CrossRefGoogle Scholar
Ganikhodjaev, N. N.. The lattice models on the Cayley tree, the quadratic processes and operator algebras. Doctoral Thesis (Rehabilitation Degree), Institute for Low Temperature Physics and Engineering Academy of Sciences of Ukraine, Kharkov, 1991.Google Scholar
Harary, F.. Graph Theory. Addison-Wesley, Reading, MA, 1969.CrossRefGoogle Scholar
Hofbauer, J. and Sigmund, K.. Evolutionary Games and Population Dynamics. Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
Jenks, R. D.. Quadratic differential systems for interactive population models. J. Differential Equations 5 (1969), 497–514.CrossRefGoogle Scholar
Kesten, H.. Quadratic transformations: a model for population growth. I. Adv. Appl. Prob. 2 (1970), 1–82.CrossRefGoogle Scholar
Losert, V. and Akin, E.. Dynamics of games and genes: discrete versus continuous time. J. Math. Biol. 17 (1983), 241–251.CrossRefGoogle Scholar
Lyubich, Yu. I.. Mathematical Structures in Population Genetics (Biomathematics, 22). Springer, Berlin, 1992.CrossRefGoogle Scholar
Lyubich, Yu. I.. Basic concepts and theorems of the evolution genetics of free populations. Russian Math. Surveys 26(5) (1978), 51–116.CrossRefGoogle Scholar
Nagylaki, T.. Evolution of a large population under gene conversion. Proc. Natl. Acad. Sci. USA 80 (1983), 5941–5945.CrossRefGoogle ScholarPubMed
Nagylaki, T.. Evolution of a finite population under gene conversion. Proc. Natl. Acad. Sci. USA 80 (1983), 6278–6281.CrossRefGoogle ScholarPubMed
Ulam, S.. A Collection of Mathematical Problems. Interscience Publishers, New York, 1960.Google Scholar
Volterra, V.. Variations and Fluctuations of the Number of Individuals in Animal Species Living Together in Animal Ecology. Ed. Chapman, R. N.. Chapman, Animal Ecology, New York, 1931.Google Scholar
Zakharevich, M. I.. On behavior of trajectories and the ergodic hypothesis for quadratic transformations of the simplex. Russian Math. Surveys 33 (1978), 265–266.CrossRefGoogle Scholar