Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-17T08:19:12.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Buoyancy instability of homologous implosions

Published online by Cambridge University Press:  15 June 2015

B. M. Johnson
B. M. Johnson*
Affiliation:
Lawrence Livermore National Laboratory, Livermore, CA 94550, USA
*
†Email address for correspondence: johnson359@llnl.gov
Get access Rights & Permissions [Opens in a new window]

Abstract

I consider the hydrodynamic stability of imploding ideal gases as an idealized model for inertial confinement fusion capsules, sonoluminescent bubbles and the gravitational collapse of astrophysical gases. For oblate modes (short-wavelength incompressive modes elongated in the direction of the mean flow), a second-order ordinary differential equation is derived that can be used to assess the stability of any time-dependent flow with planar, cylindrical or spherical symmetry. Upon further restricting the analysis to homologous flows, it is shown that a monatomic gas is governed by the Schwarzschild criterion for buoyant stability. Under buoyantly unstable conditions, both entropy and vorticity fluctuations experience power-law growth in time, with a growth rate that depends upon mean flow gradients and, in the absence of dissipative effects, is independent of mode number. If the flow accelerates throughout the implosion, oblate modes amplify by a factor 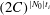$(2C)^{|N_{0}|t_{i}}$, where 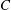$C$ is the convergence ratio of the implosion, 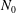$N_{0}$ is the initial buoyancy frequency and 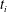$t_{i}$ is the implosion time scale. If, instead, the implosion consists of a coasting phase followed by stagnation, oblate modes amplify by a factor 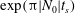$\exp ({\rm\pi}|N_{0}|t_{s})$, where 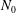$N_{0}$ is the buoyancy frequency at stagnation and 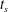$t_{s}$ is the stagnation time scale. Even under stable conditions, vorticity fluctuations grow due to the conservation of angular momentum as the gas is compressed. For non-monatomic gases, this additional growth due to compression results in weak oscillatory growth under conditions that would otherwise be buoyantly stable; this over-stability is consistent with the conservation of wave action in the fluid frame. The above analytical results are verified by evolving the complete set of linear equations as an initial value problem, and it is demonstrated that oblate modes are the fastest-growing modes and that high mode numbers are required to reach this limit (Legendre mode 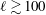$\ell \gtrsim 100$ for spherical flows). Finally, comparisons are made with a Lagrangian hydrodynamics code, and it is found that a numerical resolution of 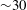${\sim}30$ zones per wavelength is required to capture these solutions accurately. This translates to an angular resolution of 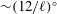${\sim}(12/\ell )^{\circ }$, or 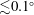${\lesssim}0.1^{\circ }$ to resolve the fastest-growing modes.

JFM classification

Compressible Flows: Compressible Flows Instability: Instability Drops and Bubbles: Sonoluminescence
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 774 , 10 July 2015 , R4
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atzeni, S. & Meyer-ter-Vehn, J. 2004 The Physics of Inertial Fusion. Oxford University Press.Google Scholar
Basko, M. & Murakami, M. 1998 Self-similar implosions and explosions of radiatively cooling gaseous masses. Phys. Plasmas 5, 518–528.Google Scholar
Betti, R., Goncharov, V. N., McCrory, R. L. & Verdon, C. P. 1998 Growth rates of the ablative Rayleigh–Taylor instability in inertial confinement fusion. Phys. Plasmas 5, 1446–1454.Google Scholar
Cao, Y. & Lou, Y.-Q. 2009 Perturbation analysis of a general polytropic homologously collapsing stellar core. Mon. Not. R. Astron. Soc. 400, 491–495.Google Scholar
Cao, Y. & Lou, Y.-Q. 2010 Adiabatic perturbations in homologous conventional polytropic core collapses of a spherical star. Mon. Not. R. Astron. Soc. 403, 491–495.Google Scholar
Cerjan, C., Springer, P. T. & Sepke, S. M. 2013 Integrated diagnostic analysis of inertial confinement fusion capsule performance. Phys. Plasmas 20, 056319.Google Scholar
Chimonas, G. 1970 The extension of the Miles–Howard theorem to compressible fluids. J. Fluid Mech. 43, 833–836.Google Scholar
Chu, M.-C. 1996 Homologous contraction of a sonoluminescing bubble. Phys. Rev. Lett. 76, 4632–4635.Google Scholar
Cook, R., McQuillan, B., Takagi, M. & Stephens, R. 2000 The development of plastic mandrels for NIF targets. ICF Semiannual Report 1, 1–12.Google Scholar
Clark, D. S., Hinkel, D. E., Eder, D. C., Jones, O. S., Haan, S. W., Hammel, B. A., Marinak, M. M., Milovich, J. L., Robey, H. F., Suter, L. J. & Town, R. P. J. 2013 Detailed implosion modeling of deuterium–tritium layered experiments on the National Ignition Facility. Phys. Plasmas 20, 056318.Google Scholar
Gatu Johnson, M., Casey, D. T., Frenje, J. A., Li, C.-K., Sguin, F. H., Petrasso, R. D., Ashabranner, R., Bionta, R., LePape, S., McKernan, M., Mackinnon, A., Kilkenny, J. D., Knauer, J. & Sangster, T. C. 2013 Measurements of collective fuel velocities in deuterium–tritium exploding pusher and cryogenically layered deuterium–tritium implosions on the NIF. Phys. Plasmas 20, 042707.Google Scholar
Goldreich, P. & Weber, S. V. 1980 Homologously collapsing stellar cores. Astrophys. J. 238, 991–997.Google Scholar
Greenspan, H. P. & Benney, D. J. 1963 On shear-layer instability, breakdown and transition. J. Fluid Mech. 15, 133–153.Google Scholar
Janka, H.-T. 2012 Explosion mechanisms of core-collapse supernovae. Annu. Rev. Nucl. Part. Sci. 62, 407–451.CrossRefGoogle Scholar
Johnson, B. M. & Gammie, C. F. 2005 Linear theory of thin, radially stratified disks. Astrophys. J. 626, 978–990.Google Scholar
Johnson, B. M. 2014 On the interaction between turbulence and a planar rarefaction. Astrophys. J. 784, 117.Google Scholar
Kidder, R. E. 1974 Theory of homogeneous isentropic compression and its application to laser fusion. Nucl. Fusion 14, 53–60.Google Scholar
Lai, D. & Goldreich, P. 2000 Growth of perturbations in gravitational collapse and accretion. Astrophys. J. 535, 402–411.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics. Butterworth-Heinemann.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.Google Scholar
Mjolsness, R. C. & Ruppel, H. M.1978 Shear-layer instability in cylindrical implosions of rotating fluids. Tech. Rep. LA-7432-MS. Los Alamos Scientific Laboratory.Google Scholar
Murphy, T. J. 2014 The effect of turbulent kinetic energy on inferred ion temperature from neutron spectra. Phys. Plasmas 21, 072701.Google Scholar
Rathkopf, J. A., Miller, D. S., Owen, J. M., Stuart, L. M., Zika, M. R., Eltgroth, P. G., Madsen, N. K., McCandless, K. P., Nowak, P. F., Nemanic, M. K., Gentile, N. A. & Keen, N. D.2000 KULL: LLNL’s ASCI inertial confinement fusion simulation code. Physor 2000, ANS Int. Topical Mtg. Adv. in Reactor Phys. Math. Comput. into the Next Millennium.Google Scholar
Sanz, J., Garnier, J., Cherfils, C., Masse, L. & Temporal, M. 2005 Self-consistent analysis of the hot spot dynamics for inertial confinement fusion capsules. Phys. Plasmas 12, 112702.Google Scholar
Schwarzschild, K. 1992 Collected Works. Springer.Google Scholar
Suslick, K. S. & Flannigan, D. J. 2008 Inside a collapsing bubble: sonoluminescence and the conditions during cavitation. Annu. Rev. Phys. Chem. 59, 659–683.Google Scholar
Thomas, V. A. & Kares, R. J. 2012 Drive asymmetry and the origin of turbulence in an ICF implosion. Phys. Rev. Lett. 109, 075004.Google Scholar
Weber, C. R., Clark, D. S., Cook, A. W., Busby, L. E. & Robey, H. F. 2014 Inhibition of turbulence in inertial-confinement-fusion hot spots by viscous dissipation. Phys. Rev. E 89, 053106.Google Scholar
Whitham, G. B. 1965 A general approach to linear and non-linear dispersive waves using a Lagrangian. J. Fluid Mech. 22, 273–283.Google Scholar