We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 22 May 2015
Let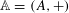 
$\mathbb{A}=(A,+)$ be a (possibly non-commutative) semigroup. For 
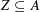$Z\subseteq A$, we define 
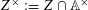$Z^{\times }:=Z\cap \mathbb{A}^{\times }$, where 
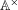$\mathbb{A}^{\times }$ is the set of the units of 
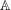$\mathbb{A}$ and The paper investigates some properties of 
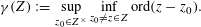$$\begin{eqnarray}{\it\gamma}(Z):=\sup _{z_{0}\in Z^{\times }}\inf _{z_{0}\neq z\in Z}\text{\text{ord}}(z-z_{0}).\end{eqnarray}$$
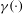${\it\gamma}(\cdot )$ and shows the following extension of the Cauchy–Davenport theorem: if 
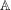$\mathbb{A}$ is cancellative and 
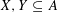$X,Y\subseteq A$, then This implies a generalization of Kemperman’s inequality for torsion-free groups and strengthens another extension of the Cauchy–Davenport theorem, where 
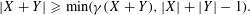$$\begin{eqnarray}|X+Y|\geqslant \min ({\it\gamma}(X+Y),|X|+|Y|-1).\end{eqnarray}$$
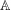$\mathbb{A}$ is a group and 
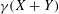${\it\gamma}(X+Y)$ in the above is replaced by the infimum of 
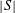$|S|$ as 
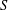$S$ ranges over the non-trivial subgroups of 
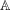$\mathbb{A}$ (Hamidoune–Károlyi theorem).
