Hostname: page-component-6b989bf9dc-94dtm Total loading time: 0 Render date: 2024-04-15T01:23:36.769Z Has data issue: false hasContentIssue false
  • English
  • Français

Gelfand pairs and strong transitivity for Euclidean buildings

Published online by Cambridge University Press:  13 March 2014

PIERRE-EMMANUEL CAPRACE  and
CORINA CIOBOTARU
PIERRE-EMMANUEL CAPRACE
Affiliation:
Université catholique de Louvain, IRMP, Chemin du Cyclotron 2, bte L7.01.02, 1348 Louvain-la-Neuve, Belgium
CORINA CIOBOTARU
Affiliation:
Université catholique de Louvain, IRMP, Chemin du Cyclotron 2, bte L7.01.02, 1348 Louvain-la-Neuve, Belgium
Get access Rights & Permissions [Opens in a new window]

Abstract

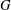Let $G$ be a locally compact group acting properly, by type-preserving automorphisms on a locally finite thick Euclidean building 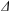$\Delta $, and 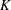$K$ be the stabilizer of a special vertex in $\Delta $. It is known that 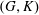$(G, K)$ is a Gelfand pair as soon as 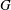$G$ acts strongly transitively on 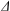$\Delta $; in particular, this is the case when 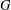$G$ is a semi-simple algebraic group over a local field. We show a converse to this statement, namely that if 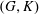$(G, K)$ is a Gelfand pair and 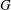$G$ acts cocompactly on $\Delta $, then the action is strongly transitive. The proof uses the existence of strongly regular hyperbolic elements in 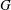$G$ and their peculiar dynamics on the spherical building at infinity. Other equivalent formulations are also obtained, including the fact that 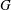$G$ is strongly transitive on 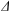$\Delta $ if and only if it is strongly transitive on the spherical building at infinity.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 4 , June 2015 , pp. 1056 - 1078
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amann, O.. Group of tree-automorphisms and their unitary representations. PhD Thesis, ETH Zürich, 2003.Google Scholar
Abramenko, P. and Brown, K. S.. Buildings: Theory and Applications (Graduate Texts in Mathematics, 248). Springer, New York, 2008.CrossRefGoogle Scholar
Abramenko, P., Parkinson, J. and Van Maldeghem, H.. A classification of commutative parabolic Hecke algebras. J. Algebra 385 (2013), 115–133.CrossRefGoogle Scholar
Ballmann, W.. Lectures on Spaces of Nonpositive Curvature (DMV Seminar, 25). Birkhäuser, Basel, 1995, with an appendix by Misha Brin.CrossRefGoogle Scholar
Ballmann, W. and Brin, M.. Orbihedra of nonpositive curvature. Publ. Math. Inst. Hautes Études Sci. 82 (1995), 169–209.CrossRefGoogle Scholar
Benoist, Y. and Labourie, F.. Sur les difféomorphismes d’Anosov affines à feuilletages stable et instable différentiables. Invent. Math. 111(2) (1993), 285–308.CrossRefGoogle Scholar
Bridson, M. and Haefliger, A.. Metric Spaces of Non-Positive Curvature. Springer, Berlin, 1999, p. 319.CrossRefGoogle Scholar
Burger, M. and Mozes, S.. Groups acting on trees: from local to global structure. Publ. Math. Inst. Hautes Études Sci. 92 (2000), 113–150.CrossRefGoogle Scholar
Caprace, P.-E. and Monod, N.. Isometry groups of non-positively curved spaces: structure theory. J. Topol. 2(4) (2009), 661–700.CrossRefGoogle Scholar
Caprace, P.-E. and Monod, N.. Fixed points and amenability in non-positive curvature. Math. Ann. 356(4) (2013), 1303–1337.CrossRefGoogle Scholar
Figà-Talamanca, A. and Nebbia, C.. Harmonic Analysis and Representation Theory for Groups Acting on Homogeneous Trees (London Mathematical Society Lecture Note Series, 162). Cambridge University Press, Cambridge, 1991.CrossRefGoogle Scholar
Garrett, P.. Buildings and Classical Groups. Chapman & Hall, London, 1997.CrossRefGoogle Scholar
Lécureux, J.. Hyperbolic configurations of roots and Hecke algebras. J. Algebra 323 (2010), 1454–1467.CrossRefGoogle Scholar
Leeb, B.. A Characterization of Irreducible Symmetric Spaces and Euclidean Buildings of Higher Rank by their Asymptotic Geometry (Bonner Mathematische Schriften [Bonn Mathematical Publications], 326). Universität Bonn Mathematisches Institut, Bonn, 2000.Google Scholar
Matsumoto, H.. Analyse harmonique dans les systèmes de Tits bornologiques de type affine (Lecture Notes in Mathematics, 590). Springer, Berlin, 1977.CrossRefGoogle Scholar
Ol’šanskiĭ, G. I.. Classification of the irreducible representations of the automorphism groups of Bruhat–Tits trees. Funkcional. Anal. i Priložen. 11(1) (1977), 32–42 ; 96 (in Russian).Google Scholar
Parkinson, J.. Buildings and Hecke algebras. J. Algebra 297(1) (2006), 1–49.CrossRefGoogle Scholar
Prasad, G. and Raghunathan, M. S.. Cartan subgroups and lattices in semi-simple groups. Ann. of Math. (2) 96 (1972), 296–317.CrossRefGoogle Scholar
Ronan, M.. Lectures on Buildings. Academic Press, Boston, 1989.Google Scholar
Swenson, E. L.. A cut point theorem for CAT(0) groups. J. Differential Geom. 53(2) (1999), 327–358.CrossRefGoogle Scholar
van Dijk, G.. Introduction to Harmonic Analysis and Generalized Gelfand Pairs (Walter de Gruyter Studies in Mathematics, 36). Walter de Gruyer, Berlin, 2009.CrossRefGoogle Scholar