Hostname: page-component-6b989bf9dc-pkhfk Total loading time: 0 Render date: 2024-04-15T03:54:18.878Z Has data issue: false hasContentIssue false
  • English
  • Français

Classifying Polygonal Algebras by their K0-Group

Part of: $K$-theory and operator algebras Selfadjoint operator algebras

Published online by Cambridge University Press:  13 February 2015

Johan Konter  and
Alina Vdovina
Johan Konter
Affiliation:
Department of Mathematics, Northwestern University, Evanston, IL 60208-2370
Alina Vdovina
Affiliation:
School of Mathematics and Statistics, University of Newcastle, Newcastle upon Tyne, NE1 7RU, alina.vdovina@ncl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that every incidence graph of a finite projective plane allows a partitioning into incident point-line pairs. This is used to determine the order of the identity in the K0-group of so-called polygonal algebras associated with cocompact group actions on Ã2-buildings with three orbits. These C*-algebras are classified by the K0-group and the class 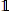of the identity in K0. To be more precise, we show that 2(q − 1) 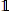= 0, where q is the order of the links of the building. Furthermore, if q = 22l−1 with l ∈ ℤ, then the order of 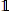is q − 1.

Keywords

Euclidean buildingsKuntz–Krieger algebrasincidence graphsfinite projective planes

MSC classification

Primary: 46L80: $K$-theory and operator algebras (including cyclic theory)
Secondary: 19K99: None of the above, but in this section
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 58 , Issue 2 , June 2015 , pp. 485 - 497
Copyright
Copyright © Edinburgh Mathematical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Anantharaman-Delaroche, C.C*-algèbres de Cuntz-Krieger et groupes Fuchsiens, in Proc. 16th Conf. Operator Theory: Operator Algebras and Related Topics, Timişoara, Romania, July 2–10, 1996, pp. 17–35 (Theta Foundation, Bucharest, 1997).Google Scholar
2.Brown, K.Buildings (Springer, 1989).CrossRefGoogle Scholar
3.Brown, L.Green, P. AND Rieffel, M.Stable isomorphism and strong Morita equivalence of C*-algebras, Pac. J. Math. 71(2) (1977), 349–363.CrossRefGoogle Scholar
4.Cartwight, D.Mantero, A.Steger, T. AND Zappa, A.Groups acting simply transitively on the vertices of a building of type Ã2, I, Geom. Dedicata 47(2) (1993), 143–166.CrossRefGoogle Scholar
5.Cartwight, D.Mantero, A.Steger, T. AND Zappa, A.Groups acting simply transitively on the vertices of a building of type Ã2, II: the cases q = 2 and q = 3, Geom. Dedicata 47(2) (1993), 167–223.CrossRefGoogle Scholar
6.Cartwright, D.Młotkowski, W. AND Steger, T.Property (T) and Ã2 groups, Annales Inst. Fourier 44(1) (1994), 213–248.CrossRefGoogle Scholar
7.Connes, A.Cyclic cohomology and the transverse fundamental class of a foliation, in Geometric Methods in Operator Algebras, Kyoto, 1983, Pitman Research Notes in Mathematics Series, Volume 123, pp. 52–144 (Longman, 1986).Google Scholar
8.Cornelissen, G.Lorscheid, O. AND Marcolli, M.On the K-theory of graph C*-algebras, Acta Appl. Math. 102(1) (2008), 57–69.CrossRefGoogle Scholar
9.Moriyoshi, H. AND Natsume, T.The Godbillon-Vey cocycle and longitudinal Dirac operators, Pac. J. Math. 172 (1996), 483–539.Google Scholar
10.Natsume, T.Euler characteristic and the class of unit in K-theory, Math. Z. 194 (1987), 237–243.CrossRefGoogle Scholar
11.Phillips, N.C.A classification theorem for nuclear purely infinite simple C*-algebras, Documenta Math. 5 (2000), 49–114.CrossRefGoogle Scholar
12.Robertson, G. AND Steger, T.Affine buildings, tiling systems and higher rank Cuntz-Krieger algebras, J. Reine Angew. Math. 513 (1999), 115–144.CrossRefGoogle Scholar
13.Robertson, G. AND Steger, T.Asymptotic K-theory for groups acting on Ã2 building, Can. J. Math. 53(4) (2001), 809–833.CrossRefGoogle Scholar
14.Robertson, G. AND Steger, T.Irreducible subshifts associated with Ã2 buildings, J. Combin. Theory A 103 (2003), 91–104.CrossRefGoogle Scholar
15.Vdovina, A.Combinatoral structure of some hyperbolic buildings, Math. Z. 241(3) (2002) 471–478.CrossRefGoogle Scholar
16.Vdovina, A.Polyhedra with specified links, in Séminaire de Théorie spectrale et géométrie, Grenoble, 2002–2003, Volume 21, pp. 37–42.CrossRefGoogle Scholar