Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-16T16:58:32.341Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE NORMALISED LAPLACIAN SPECTRUM, DEGREE-KIRCHHOFF INDEX AND SPANNING TREES OF GRAPHS

Part of: Circuits, networks Graph theory

Published online by Cambridge University Press:  26 February 2015

JING HUANG  and
SHUCHAO LI
JING HUANG
Affiliation:
Faculty of Mathematics and Statistics, Central China Normal University, Wuhan 430079, PR China email 1042833291@qq.com
SHUCHAO LI*
Affiliation:
Faculty of Mathematics and Statistics, Central China Normal University, Wuhan 430079, PR China email lscmath@mail.ccnu.edu.cn
*
✉lscmath@mail.ccnu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

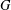Given a connected regular graph $G$, let 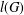$l(G)$ be its line graph, $s(G)$ its subdivision graph, $r(G)$ the graph obtained from 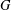$G$ by adding a new vertex corresponding to each edge of 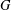$G$ and joining each new vertex to the end vertices of the corresponding edge and 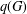$q(G)$ the graph obtained from 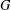$G$ by inserting a new vertex into every edge of $G$ and new edges joining the pairs of new vertices which lie on adjacent edges of 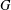$G$. 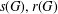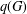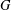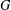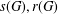A formula for the normalised Laplacian characteristic polynomial of $l(G)$ (respectively $s(G),r(G)$ and $q(G)$) in terms of the normalised Laplacian characteristic polynomial of $G$ and the number of vertices and edges of $G$ is developed and used to give a sharp lower bound for the degree-Kirchhoff index and a formula for the number of spanning trees of $l(G)$ (respectively $s(G),r(G)$ and $q(G)$).

Keywords

resistance distanceKirchhoff indexnormalised Laplacianspanning tree

MSC classification

Primary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Secondary: 94C99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 3 , June 2015 , pp. 353 - 367
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Atay, F. M. and Tuncel, H., ‘On the spectrum of the normalized Laplacian for signed graphs: interlacing, contraction, and replication’, Linear Algebra Appl. 442 (2014), 165–177.Google Scholar
Biggs, N. L., Algebraic Graph Theory (Cambridge University Press, Cambridge, 1993).Google Scholar
Bonchev, D., Balaban, A. T., Liu, X. and Klein, D. J., ‘Molecular cyclicity and centricity of polycyclic graphs I: cyclicity based on resistance distances or reciprocal distances’, Internat. J. Quantum Chem. 50 (1994), 1–20.CrossRefGoogle Scholar
Buckley, F. and Harary, F., Distance in Graphs (Addison-Wesley, Reading, MA, 1989).Google Scholar
Chandra, A. K., Raghavan, P., Ruzzo, W. L., Smolensky, R. and Tiwari, P., ‘The electrical resistance of a graph captures its commute and cover times’, in: Proc. 21st Annual ACM Symposium on Theory of Computing (Seattle, WA, 1989), 574–586.Google Scholar
Chen, H. Y. and Zhang, F. J., ‘Resistance distance and the normalized Laplacian spectrum’, Discrete Appl. Math. 155 (2007), 654–661.Google Scholar
Chung, F. R. K., Spectral Graph Theory (American Mathematical Society, Providence, RI, 1997).Google Scholar
Feng, L. H., Gutman, I. and Yu, G. H., ‘Degree Kirchhoff index of unicyclic graphs’, MATCH Commun. Math. Comput. Chem. 69 (2013), 629–648.Google Scholar
Gao, X., Luo, Y. F. and Liu, W. W., ‘Kirchhoff index in line, subdivision and total graphs of a regular graph’, Discrete Appl. Math. 160 (2012), 560–565.Google Scholar
Gutman, I. and Mohar, B. , ‘The quasi-Wiener and the Kirchhoff indices coincide’, J. Chem. Inf. Comput. Sci. 36 (1996), 982–985.CrossRefGoogle Scholar
Horn, R. A. and Johnson, C. R., Topics in Matrix Analysis (Cambridge University Press, Cambridge, 1991).Google Scholar
Kel’mans, A. K., ‘On properties of the characteristic polynomial of a graph’, in: Kibernetiku Na Sluzbu Kommunizmu, 4 (Gosenergoizdat, Moscow, 1967), 27–47 (in Russian).Google Scholar
Klein, D. J., ‘Resistance-distance sum rules’, Croat. Chem. Acta 75 (2002), 633–649.Google Scholar
Klein, D. J. and Ivanciuc, O., ‘Graph cyclicity, excess conductance, and resistance deficit’, J. Math. Chem. 30 (2001), 271–287.CrossRefGoogle Scholar
Klein, D. J. and Randić, M., ‘Resistance distance’, J. Math. Chem. 12 (1993), 81–95.CrossRefGoogle Scholar
Li, J. X., Guo, J. M., Shiu, W. C. and Chang, A., ‘An edge-separating theorem on the second smallest normalized Laplacian eigenvalue of a graph and its applications’, Discrete Appl. Math. 171 (2014), 104–115.Google Scholar
Liu, B. L. and Lai, H. J., Matrices in Combinatorics and Graph Theory (Kluwer Academic Publishers, Dordrecht, 2000).Google Scholar
Lovász, L., ‘Random walks on graphs: a survey’, in: Combinatorics, Paul Erdős is Eighty, 2 (Janos Bolyai Mathematical Society, Budapest, 1996), 353–397.Google Scholar
Palacios, J. and Renom, J. M., ‘Another look at the degree-Kirchhoff index’, Internat. J. Quantum Chem. 111 (2011), 3453–3455.CrossRefGoogle Scholar
Wang, W. Z., Yang, D. and Luo, Y. F., ‘The Laplacian polynomial and Kirchhoff index of graphs derived from regular graphs’, Discrete Appl. Math. 161 (2013), 3063–3071.Google Scholar
Wiener, H., ‘Structural determination of paraffin boiling points’, J. Amer. Chem. Soc. 69 (1947), 17–20.CrossRefGoogle ScholarPubMed
Yan, W. G., ‘On the number of spanning trees of some irregular line graphs’, J. Combin. Theory Ser. A 120 (2013), 1642–1648.Google Scholar
Zhang, F. J., Chen, Y. C. and Chen, Z. B., ‘Clique-inserted-graphs and spectral dynamics of clique-inserting’, J. Math. Anal. Appl. 349 (2009), 211–225.CrossRefGoogle Scholar
Zhu, H. Y., Klein, D. J. and Lukovits, I., ‘Extensions of the Wiener number’, J. Chem. Inf. Comput. Sci. 36 (1996), 420–428.CrossRefGoogle Scholar