Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-19T04:37:17.860Z Has data issue: false hasContentIssue false
  • English
  • Français

Théorèmes de type Fouvry–Iwaniec pour les entiers friables

Part of: Multiplicative number theory

Published online by Cambridge University Press:  03 March 2015

Sary Drappeau
Sary Drappeau*
Affiliation:
CRM – Université de Montréal, Pavillon André Aisenstadt, 2920 ch. de la Tour, Montréal, H3T 1J4 QC, Canada email drappeaus@dms.umontreal.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An integer $n$ is said to be 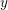$y$-friable if its largest prime factor 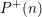$P^{+}(n)$ is less than 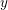$y$. In this paper, it is shown that the 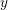$y$-friable integers less than $x$ have a weak exponent of distribution at least 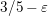$3/5-{\it\varepsilon}$ when 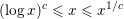$(\log x)^{c}\leqslant x\leqslant x^{1/c}$ for some 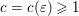$c=c({\it\varepsilon})\geqslant 1$, that is to say, they are well distributed in the residue classes of a fixed integer $a$, on average over moduli 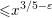${\leqslant}x^{3/5-{\it\varepsilon}}$ for each fixed 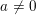$a\neq 0$ and 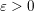${\it\varepsilon}>0$. We apply this to the estimation of the sum 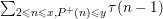$\sum _{2\leqslant n\leqslant x,P^{+}(n)\leqslant y}{\it\tau}(n-1)$ when 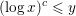$(\log x)^{c}\leqslant y$. This follows and improves on previous work of Fouvry and Tenenbaum. Our proof combines the dispersion method of Linnik in the setting of Bombieri, Fouvry, Friedlander and Iwaniec with recent work of Harper on friable integers in arithmetic progressions.

Keywords

friable integersequidistribution in arithmetic progressionsdispersion method

MSC classification

Primary: 11N25: Distribution of integers with specified multiplicative constraints
Secondary: 11N69: Distribution of integers in special residue classes
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 5 , May 2015 , pp. 828 - 862
Copyright
© The Author 2015 

References

Bombieri, E., Friedlander, J. B. and Iwaniec, H., Primes in arithmetic progressions to large moduli, Acta Math. 156 (1986), 203–251.CrossRefGoogle Scholar
Bombieri, E., Friedlander, J. B. and Iwaniec, H., Primes in arithmetic progressions to large moduli. II, Math. Ann. 277 (1987), 361–393.CrossRefGoogle Scholar
Bombieri, E., Friedlander, J. B. and Iwaniec, H., Primes in arithmetic progressions to large moduli. III, J. Amer. Math. Soc. 2 (1989), 215–224.CrossRefGoogle Scholar
Burgess, D. A., The distribution of quadratic residues and non-residues, Mathematika 4 (1957), 106–112.CrossRefGoogle Scholar
de la Bretèche, R. and Tenenbaum, G., Propriétés statistiques des entiers friables, Ramanujan J. 9 (2005), 139–202.CrossRefGoogle Scholar
Deshouillers, J.-M. and Iwaniec, H., Kloosterman sums and Fourier coefficients of cusp forms, Invent. Math. 70 (1982/83), 219–288.CrossRefGoogle Scholar
Fiorilli, D., On a theorem of Bombieri, Friedlander, and Iwaniec, Canad. J. Math. 64 (2012), 1019–1035.CrossRefGoogle Scholar
Fouvry, É., Répartition des suites dans les progressions arithmétiques, Acta Arith. 41 (1982), 359–382.CrossRefGoogle Scholar
Fouvry, É., Autour du théorème de Bombieri–Vinogradov, Acta Math. 152 (1984), 219–244.CrossRefGoogle Scholar
Fouvry, É., Sur le problème des diviseurs de Titchmarsh, J. Reine Angew. Math. 357 (1985), 51–76.Google Scholar
Fouvry, É. and Iwaniec, H., On a theorem of Bombieri–Vinogradov type, Mathematika 27 (1980), 135–152.CrossRefGoogle Scholar
Fouvry, É. and Iwaniec, H., Primes in arithmetic progressions, Acta Arith. 42 (1983), 197–218.CrossRefGoogle Scholar
Fouvry, É. and Tenenbaum, G., Diviseurs de Titchmarsh des entiers sans grand facteur premier, in Analytic number theory (Tokyo, 1988), Lecture Notes in Mathematics, vol. 1434 (Springer, Berlin, 1990), 86–102.CrossRefGoogle Scholar
Fouvry, É. and Tenenbaum, G., Répartition statistique des entiers sans grand facteur premier dans les progressions arithmétiques, Proc. Lond. Math. Soc. (3) 72 (1996), 481–514.CrossRefGoogle Scholar
Granville, A., Integers, without large prime factors, in arithmetic progressions. I, Acta Math. 170 (1993), 255–273.CrossRefGoogle Scholar
Granville, A., Integers, without large prime factors, in arithmetic progressions. II, Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 345 (1993), 349–362.Google Scholar
Harper, A. J., On a paper of K. Soundararajan on smooth numbers in arithmetic progressions, J. Number Theory 132 (2012), 182–199.CrossRefGoogle Scholar
Harper, A. J., Bombieri–Vinogradov and Barban-Davenport-Halberstam type theorems for smooth numbers, Preprint (2012), arXiv:1208.5992.Google Scholar
Hildebrand, A., Integers free of large prime factors and the Riemann hypothesis, Mathematika 31 (1984), 258–271.CrossRefGoogle Scholar
Hildebrand, A., Integers free of large prime divisors in short intervals, Q. J. Math 36 (1985), 57–69.CrossRefGoogle Scholar
Hildebrand, A., On the number of positive integers ⩽x and free of prime factors > y, J. Number Theory 22 (1986), 289–307.CrossRefGoogle Scholar
Hildebrand, A. and Tenenbaum, G., On integers free of large prime factors, Trans. Amer. Math. Soc. 296 (1986), 265–290.CrossRefGoogle Scholar
Hildebrand, A. and Tenenbaum, G., Integers without large prime factors, J. Théor. Nombres Bordeaux 5 (1993), 411–484.CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory, Colloquium Publications, vol. 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Saias, É., Sur le nombre des entiers sans grand facteur premier, J. Number Theory 32 (1989), 78–99.CrossRefGoogle Scholar
Sarnak, P., Selberg’s eigenvalue conjecture, Notices Amer. Math. Soc. 42 (1995), 1272–1277.Google Scholar
Soundararajan, K., The distribution of smooth numbers in arithmetic progressions, in Anatomy of integers, CRM Proceedings & Lecture Notes, vol. 46 (American Mathematical Society, Providence, RI, 2008), 115–128.CrossRefGoogle Scholar
Tenenbaum, G., Introduction à la théorie analytique et probabiliste des nombres, Collection Échelles, third edition (Belin, 2008).Google Scholar
Weil, A., On some exponential sums, Proc. Natl. Acad. Sci. USA 34 (1948), 204.CrossRefGoogle ScholarPubMed
Wolke, D., Über die mittlere Verteilung der Werte zahlentheoretischer Funktionen auf Restklassen. I, Math. Ann. 202 (1973), 1–25.CrossRefGoogle Scholar