Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-23T06:21:55.268Z Has data issue: false hasContentIssue false
  • English
  • Français

RADICAL RELATED TO SPECIAL ATOMS REVISITED

Part of: Radicals and radical properties of rings

Published online by Cambridge University Press:  14 October 2014

HALINA FRANCE-JACKSON ,
SRI WAHYUNI  and
INDAH EMILIA WIJAYANTI
HALINA FRANCE-JACKSON*
Affiliation:
Department of Mathematics and Applied Mathematics, Summerstrand Campus (South), PO Box 77000, Nelson Mandela Metropolitan University, Port Elizabeth 6031, South Africa email cbf@easterncape.co.uk
SRI WAHYUNI
Affiliation:
Jurusan Matematika, FMIPA UGM, Sekip Utara, Yogyakarta-Indonesia email swahyuni@ugm.ac.id
INDAH EMILIA WIJAYANTI
Affiliation:
Jurusan Matematika, FMIPA UGM, Sekip Utara, Yogyakarta-Indonesia email ind_wijayanti@ugm.ac.id
*
✉cbf@easterncape.co.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A semiprime ring 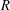$R$ is called a $\ast$-ring if the factor ring 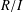$R/I$ is in the prime radical for every nonzero ideal 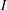$I$ of 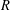$R$. A long-standing open question posed by Gardner asks whether the prime radical coincides with the upper radical 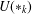$U(\ast _{k})$ generated by the essential cover of the class of all $\ast$-rings. This question is related to many other open questions in radical theory which makes studying properties of 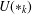$U(\ast _{k})$ worthwhile. We show that 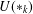$U(\ast _{k})$ is an N-radical and that it coincides with the prime radical if and only if it is complemented in the lattice 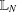$\mathbb{L}_{N}$ of all N-radicals. Along the way, we show how to establish left hereditariness and left strongness of important upper radicals and give a complete description of all the complemented elements in 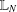$\mathbb{L}_{N}$.

Keywords

∗-ringextraspecial radicalprime radicalessential idealessential coverspecial classspecial and supernilpotent radicalsN-radicals complemented radicalsspecial atoms

MSC classification

Primary: 16N80: General radicals and rings
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 2 , April 2015 , pp. 202 - 210
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Andrunakievich, V. A. and Ryabukhin, Yu. M., Radicals of Algebra and Structure Theory (Nauka, Moscow, 1979) (in Russian).Google Scholar
Beidar, K. I. and Salavova, K., ‘On lattices of N-radicals, left strong radicals, left hereditary radicals’, Acta Math. Hungar. 42(1–2) (1983), 81–95 (in Russian).Google Scholar
Beidar, K. I., Fong, Y. and Ke, W. E., ‘On complemented radicals’, J. Algebra 201 (1998), 328–356.Google Scholar
Birkhoff, G., Lattice Theory, 3rd edn (American Mathematical Society, Providence, RI, 1967).Google Scholar
Divinsky, N. and Sulinski, A., ‘Radical pairs’, Canad. J. Math. 29(5) (1977), 1086–1091.Google Scholar
Divinsky, N., Krempa, J. and Sulinski, A., ‘Strong radical properties of alternative and associative rings’, J. Algebra 17 (1971), 369–388.Google Scholar
France-Jackson, H., ‘∗-rings and their radicals’, Quaest. Math. 8 (1985), 231–239.Google Scholar
France-Jackson, H., ‘On atoms of the lattice of supernilpotent radicals’, Quaest. Math. 10 (1987), 251–256.Google Scholar
France-Jackson, H., ‘On special atoms’, J. Aust. Math. Soc. (Ser. A) 64 (1998), 302–306.Google Scholar
France-Jackson, H., ‘Rings related to special atoms’, Quaest. Math. 24 (2001), 105–109.CrossRefGoogle Scholar
France-Jackson, H., ‘On left (right) strong and left (right) hereditary radicals’, Quaest. Math. 29 (2006), 329–334.Google Scholar
France-Jackson, H., ‘On supernilpotent radicals with the Amitsur property’, Bull. Aust. Math. Soc. 80 (2009), 423–429.Google Scholar
France-Jackson, H. and Leavitt, W. G., ‘On 𝛽-classes’, Acta Math. Hungar. 90(3) (2001), 243–252.Google Scholar
Gardner, B. J., ‘Some recent results and open problems concerning special radicals’, in: Radical Theory: Proceedings of the 1988 Sendai Conference (ed. Kyuno, S.) (Uchida Rokakuho, Tokyo) 25–56.Google Scholar
Gardner, B. J. and Wiegandt, R., Radical Theory of Rings (Marcel Dekker, New York, 2004).Google Scholar
Jaegermann, M., ‘Normal radicals’, Fund. Math. 95 (1977), 147–155.Google Scholar
Jaegermann, M. and Sands, A. D., ‘On normal radicals and normal classes of rings’, J. Algebra 50 (1978), 337–349.CrossRefGoogle Scholar
Kaplansky, I., Commutative Rings (Allyn and Bacon, Boston, MA, 1970).Google Scholar
Korolczuk, H., ‘A note on the lattice of special radicals’, Bull. Pol. Acad. Sci. Math. 29 (1981), 103–104.Google Scholar
Krachilov, K. K., ‘Complements in the lattice of supernilpotent radicals I’, Mat. Issled. Kishinev 49 (1979), 87–104 (in Russian).Google Scholar
Krachilov, K. K., ‘Complementedness in lattices of radicals I’, Mat. Issled. Kishinev 62 (1981), 76–88 (in Russian).Google Scholar
Krachilov, K. K., ‘Complementedness in lattices of radicals II’, Mat. Issled. Kishinev 62 (1981), 89–111 (in Russian).Google Scholar
Procesi, C., ‘Noncommutative Jacobson rings’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 21 (1967), 281–290.Google Scholar
Puczylowski, E. R., ‘On normal classes of rings’, Comm. Algebra 20 (1992), 2999–3013.CrossRefGoogle Scholar
Puczylowski, E. R. and Roszkowska, E., ‘Atoms of lattices of associative rings’, in: Radical Theory: Proceedings of the 1988 Sendai Conference (ed. Kyuno, S.) (Uchida Rokakuho, Tokyo) 123–134.Google Scholar
Sands, A. D., ‘Radicals and Morita context’, J. Algebra 24 (1973), 335–345.Google Scholar
Sands, A. D., ‘On normal radicals’, J. Lond. Math. Soc. (2) 11 (1975), 361–365.Google Scholar
Snider, R. L., ‘Complemented hereditary radicals’, Bull. Aust. Math. Soc. 4 (1971), 307–320.Google Scholar
Snider, R. L., ‘Lattices of radicals’, Pacific J. Math. 40 (1972), 207–220.Google Scholar
Watters, J. F., ‘Polynomial extension of Jacobson rings’, J. Algebra 36 (1975), 302–308.Google Scholar
Watters, J. F., ‘The Brown–McCoy radical and Jacobson rings’, Bull. Acad. Polon. Sci. 24 (1976), 91–100.Google Scholar