1. INTRODUCTION
Conceptual design is the earliest stage in the overall process of engineering system design. Past research efforts (Ormon et al., Reference Ormon, Cassady and Greenwood2002; Jen, Reference Jen2005; Leveson et al., Reference Leveson, Dulac, Zipkin, Cutcher, Carroll and Barrett2006; Madni & Jackson, Reference Madni and Jackson2009; Kurtoglu et al., Reference Kurtoglu, Tumer and Jensen2010) have recognized the significance of utilizing fault-tolerance analysis during the conceptual design phase. However, anticipating component failure rates and system performance is difficult because detailed knowledge of system components and their performance criteria are not yet available. Therefore, it is important to develop fault-tolerance engineering tools that can be used during the early design of complex systems because of the inherent uncertainty in the performance of individual components and their interaction effects during the product life cycle cost (Zhang et al., Reference Zhang, Kurtoglu, Tumer and O'Halloran2011). Robustness in this context means operation of the system within the designed performance variance under all ranges of environmental conditions experienced in the field. For the engineered system to be robust, the design of the system is required to be robust, meaning that the system is able to function under the full range of environmental conditions that may be experienced during system operation (Youn & Wang, Reference Youn, Hu and Wang2011). Resiliency is recognized as maintaining system functions despite the existence of failures (Mehrpouyan, Reference Mehrpouyan2013). This differs from traditional definitions of robustness because resiliency deals with the functional response of a system. As designers, it is important to be sure that these systems are able to perform the functions they were designed to perform; something that robustness does not strictly deal with. Instead, robustness correlates to the ability of a system to produce performance characteristics despite the presence of these internal and external stimuli. Complete functionality of a complex engineered system does not necessarily have to be maintained for the system to be considered robust.
The main purpose of system reliability analysis is to determine the weakness of a design and to quantify the impact of component failures. The resulting analysis provides a numerical rank to identify which components are more important to system reliability enhancement or more critical to system failure. Design reliability analysis methods introduced in the research literature, such as the function-failure design (Stone et al., Reference Stone, Tumer and Van Wie2005), the functional failure identification and propagation (Kurtoglu & Tumer, Reference Kurtoglu and Tumer2008), and decomposition-based design optimization (McCulley & Bloebaum, Reference McCulley and Bloebaum1996; Michelena et al., Reference Michelena and Panos1997) methods have begun to adopt graph-based approaches to model the function of the component and the flow of energy, material, and signal (EMS) between them. This work extends this idea to demonstrate the effect of the design architecture on the robustness of the system being designed.
In the past several years, scientific interest has been devoted to modeling and characterization of complex systems that are defined as networks. Such systems consist of simple components whose interactions are very basic, but their large-scale effects are extremely complex (e.g., protein webs, social communities, and the Internet). Numerous research studies have been devoted to the effect of network architecture on the system dynamics, behavior, and characteristics. Because many complex engineered systems can be represented by their internal product architecture, their complexity is dependent on the heterogeneity and quantity of different components as well as the formation of connections between those components. Because of this, system properties can be studied by graph-theoretic approaches. Complex networks are modeled with graph-based approaches, which are effective in representing components and their underlying interactions within complex engineered systems.
Research findings by Ash and Newth (Reference Ash and Newth2007) suggest that modular systems are less robust even though their individual components are designed with high robustness. Modularity describes the topology of a system or network. Modularity in a system is rather straightforward. A system is modular if components or subsystems can be isolated from the greater system without compromising the structure of the rest of the system. For instance, a modular system topology is one that allows a component or subsystem to be removed without first removing many others. Networks are a little more difficult. A network is said to be modular if there are high concentrations of high connectedness in the network separated by low connectedness between “modules.” Bagrow et al. (Reference Bagrow, Lehmann and Ahn2011) confirm these finding and further explain that the high robustness of modular systems is only possible if the components' failure can be isolated to their modules. Furthermore, Hölttä et al. (Reference Hölttä, Suh and de Weck2005) prove that while the hierarchical modular structure improves the system's robustness, excessive use of modularity results in loss of performance. In contrast, there are studies (Gershenson et al., Reference Gershenson, Prasad and Zhang2003; Ishii & Yang, Reference Ishii and Yang2003) that support the increase of modularity in the design of complex engineered systems. Therefore, in order to design a robust system and to recommend or oppose the modular physical system architecture, it is utterly important to understand the architectural properties of complex engineered systems and the effect of design architecture topology on the propagation of failures within a complex engineered system.
In this research, we adopt approaches from graph theory and social network analysis to understand the robustness of the design architecture of a complex engineered system. Specifically, this paper shows the relationship between graph spectral theory eigenvalue analysis and how optimizing (or altering) the graph of a system will change system connectedness, thereby changing the robustness of the system. To accomplish this objective, the network model of a safety-critical engineered system in the context of complex network theory is constructed. Its network properties are calculated to determine system robustness. Constructive design architecture change recommendations are made to optimize the system robustness.
2. BACKGROUND
Eliminating the likelihood of failures and, should failures occur, ensuring the continued operation of the system within a safe performance envelop until repairs can be made are of paramount importance in mission critical complex engineered systems. To avoid the failures of critical components, setting aside the problem of identifying critical components, the engineering design literature recommends techniques such as failure mode effects analysis (Stamatis, Reference Stamatis2003) or a function-failure design method (Stone et al., Reference Stone, Tumer and Van Wie2005), among many. Although these techniques have proven useful where knowledge of failure modes and effects can be predicted, their most significant weaknesses are that they can neither readily handle interaction effects of failures nor identify the most vulnerable components without significant prior knowledge. Although methods such as the functional failure identification and propagation technique address this issue (Kurtoglu & Tumer, Reference Kurtoglu and Tumer2008), significant expertise of engineers and a knowledge base of previous products are still required.
In contrast to techniques relying on prior knowledge, the network topology analysis and biological concepts of resilience hold promise for addressing this problem in the engineering design domain. The study of network topologies provides interesting insights into the way that complex engineered systems are designed. Numerous studies (Albert et al., Reference Albert, Jeong and Barabási2000; Crucitti et al., Reference Crucitti, Latora, Marchiori and Rapisarda2004) have attempted to measure the resilience of complex networks. In the design of networks, the design philosophy is not to predict that failures will occur, but, rather, to design with the knowledge that failures will occur (i.e., that nodes will fail and external “attacks” on the network may happen). The challenge for the network designer is to ensure that the network continues to operate, or fails gracefully, even under such circumstances. The results of these efforts conclude that many complex systems exhibit a surprising degree of tolerance against failure in a specific class of networks called scale-free networks (Goh et al., Reference Goh, Oh, Jeong, Kahng and Kim2002). A scale-free network is an inhomogeneous network in nature, meaning that a significant number of nodes have very few connections while a small number of particular nodes have many connections. The inhomogeneous feature of a scale-free network allows for higher failure tolerance under random failure of nodes, but the network is more vulnerable to failure when the most highly connected nodes fail (Callaway et al., Reference Callaway, Newman, Strogatz and Watts2000; Cohen et al., Reference Cohen, Erez, Ben-Avraham and Havlin2000; Jeong et al., Reference Jeong, Tombor, Albert, Oltvai and Barabási2000; Tu, Reference Tu2000). In the case of designing resilient complex engineered systems, the design architecture can be modeled as a complex network and their resilience optimized by ensuring that critical components (nodes) are less vulnerable to failure while preserving the interconnectedness of interdependent components.
There are two concepts that are most relevant: contagion spread and failure tolerance. A contagion spreads by altering the states of nodes, which is not dissimilar from the situation of a degraded flow from a component altering the performance of interdependent components. This is usually described as degradation in system performance, and robust systems are those that maintain performance within a tight tolerance despite perturbations. However, engineered system designs are naturally different from models such as the Internet and World Wide Web representations of complex networks. As a result, the appropriate network representation is critical to the success of modeling engineered system design, because the representation affects the accuracy and efficiency of the calculation for system modularization and optimization. In order to evaluate different system design architectures for any given design problem, the graph theoretic formulation must not depend on any particular design architecture. Therefore, a general and precise analytical model such as a nonlinear dynamical system (NLDS) that uses a system of probability equations (Callaway et al., Reference Callaway, Newman, Strogatz and Watts2000) for accurate modeling of viral propagation in complex networks can be used to investigate the behavior of failure propagation in complex engineered systems. This approach examines the propagation behavior via a number of stochastic contact trials per unit time, where the infection expands at a constant rate from an initially infected vertex.
In addition, existing research literature on the analysis of disease epidemic spreading (Moreno et al., Reference Moreno, Pastor-Satorras and Vespignani2002; Wang et al., Reference Wang, Chakrabarti, Wang and Faloutsos2003; Chakrabarti et al., Reference Chakrabarti, Wang, Wang, Leskovec and Faloutsos2008) and dynamics of information spreading in social networks (Acemoglu et al., Reference Acemoglu, Ozdaglar and ParandehGheibi2010; Lerman & Ghosh, Reference Lerman and Ghosh2010) are focused on modeling the failure propagation in complex engineered systems. Even though the two models share similar features, they are very different. For example, the disease-spreading model is based on the physical contact between individuals in a social network. Many factors such as biological characteristics of both the carrier and the infectious agent play an important role in the mathematical model of the spread. However, information spreading is possible through nonphysical contact and via the use of communication infrastructures, and the decision of whether information should be spread to more individuals or not is made by individuals. Consequently, the paper focuses on the epidemic spreading of diseases, and these types of models inspire the proposed model.
3. METHODOLOGY
The initial part of the research focuses on producing synthetic networks that model real-world system design. In order to evaluate each design, a Modelica-based structural model (Tiller, Reference Tiller2001) is created and converted into a graph representation of the system's design architecture. The network is modeled by a connected graph G = (V, E), which is a collection of vertices V (also called nodes) with edges E between them. In this context, components of complex engineered systems are modeled as nodes of the graph, and the connections between these components are the graph edges. These graph representations are then used as a tool to convert each design into an adjacency matrix of nodes (components) and edge connections. Let A signify the adjacency matrix of an engineered system under study with n components. A is defined as follows:
where Δ symbolizes the set of components, and A is a square symmetric matrix with diagonal entries of zero. The edge connections between components are defined topologically. A topologically defined graph has components that are physically connected. For example, if two components are physically connected together within a design, they are connected within the graph and are represented with a “1” within an adjacency matrix.
In addition, a degree matrix called D is used to define the number of connections associated with a specific node or component and is defined based on the following:
Then, the Laplacian matrix is defined as L = D − A for unweighted graphs.
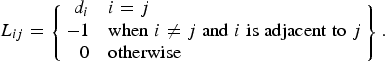 $${L_{ij}} = \left\{\matrix{\hfill{d_i} &i = j \hfill\cr - 1 & {\rm when}\; i \ne j\; {\rm and}\; i\; {\rm is}\; {\rm adjacent}\; {\rm to}\; j \cr \hfill0& {\rm otherwise}\hfill} \right\}.$$
$${L_{ij}} = \left\{\matrix{\hfill{d_i} &i = j \hfill\cr - 1 & {\rm when}\; i \ne j\; {\rm and}\; i\; {\rm is}\; {\rm adjacent}\; {\rm to}\; j \cr \hfill0& {\rm otherwise}\hfill} \right\}.$$In reviewing the literature in algebraic graph theory (Fax & Murray, Reference Fax and Murray2004; Jamakovic & Uhlig, Reference Jamakovic and Uhlig2007; Wu et al., Reference Wu, Barahona, Tan and Deng2011), the second smallest eigenvalue of the Laplacian matrix has appeared as a critical parameter for robustness properties of dynamic systems that operate as networks. The second smallest eigenvalue of a Laplacian matrix is known as the algebraic connectivity. The algebraic connectivity describes the average difficulty to isolate an individual node (component) from the rest of the system (Fig. 1). Because the algebraic connectivity of a graph increases with increasing node and edge connectivity, a higher algebraic connectivity will result in an increased number of paths between nodes. This inherently means that networks with higher algebraic connectivity are more robust (Jamakovic & Uhlig, Reference Jamakovic and Uhlig2007). In addition, another such parameter exists in the literature called spectral radius. In the review of literature from network theory, the spectral radius is the largest eigenvalue of the adjacency matrix (Jamakovic et al., Reference Jamakovic, Kooij, Van Mieghem and van Dam2006). Jamakovic et al. (Reference Jamakovic, Kooij, Van Mieghem and van Dam2006) conclude that a smaller spectral radius results in higher system resiliency against failure propagation throughout the system compared to other networks of similar average node degree. Because this value is based on the evaluation of the eigenspectrum of a single, unique characteristic equation, it is important to note that the value is not useful unless it is compared to another graph of similar size. It does not have a defined range of values. The spectral radius provides a high-level analysis to compare two or more graphs.

Fig. 1. Even though both graphs have the same degree sequence, the graph on the left is considered weakly connected. On the left, the algebraic connectivity equals 0.238, and on the right, 0.925.
The number of modules present in a network is determined using the eigenvalues of the adjacency matrix representation of the design (Sarkar & Dong, Reference Sarkar and Dong2011; Sarkar et al., Reference Sarkar, Henderson and Robinson2013). To determine the number of modules, the eigenvalues of the adjacency matrix are ordered in descending order. The differences between the ordered eigenvalues define the number of modules in the system. If k corresponds to an eigenvalue of the adjacency matrix, the maximum difference is between the kth and kth + 1 eigenvalue. The number of modules is the k value where that difference is the greatest. Given the relative quantity of modules within a design, this information can be used for insight into the robustness of a given design topology as well as the resilience to attack propagation for a specific design.
The following constraints are defined while modeling the system under design as a network:
1. A component is not connected to itself, meaning that the diagonal of the adjacency matrix is a diagonal of zeros.
2. A system is represented as a connected system; therefore, there is no isolated component (or set of components) not connected to any other component. Every node should have a path available to reach every other node in the network.
3.1. Maximizing the design robustness
This section demonstrates the effect on the design architecture from maximizing the algebraic connectivity for system robustness. A random, generic system is represented as a network. This system is not meant to describe possible real-world system architectures, but rather to show how changes in network topology manifest in graph analysis metrics. A genetic algorithm is developed to iterate through a random network and change the connections between nodes (components) within an adjacency matrix. This is done by maximizing the algebraic connectivity of the network in each iteration. Each generation (iteration) represents a system architecture that experiences binary crossover and mutation events to produce the next generation. The system under design is modeled in binary values with values of 1 representing a connection between two components, and 0 otherwise. The developed algorithm performs evaluations on a binary bit string of characters, which represent the connections between two components. Even though the Laplacian matrix is used to define the algebraic connectivity, the adjacency matrix is manipulated in order to iterate through the design space. The design space is defined by combinations of generic system components, where each component is capable of having a connection with any other component. This results in all possible system design candidate architectures, including some infeasible architecture. The evaluation process is computed on a sequence of design variables, where every possible connection between one component and another is a design variable, represented in a binary string of 1 or 0 characters similar to the following:
For a more conventional problem, such as a design problem with defined design variables, such as length, width, height, mass, and so on, the algorithm manipulates the string so that the binary address of the design variables is changed from generation to generation. This is especially useful for a discrete problem that contains only a handful of possible design architectures. Figure 2 depicts the steps of the algorithmic process to compute the algebraic connectivity of the system under design. The maximization of the algebraic connectivity in the genetic algorithm produces adjacency matrices with higher component degrees, representing a higher average number of connections per component and therefore a higher algebraic connectivity, as expected.

Fig. 2. Algorithm steps for computing the resiliency of the system under design.
3.2. Design topology and its effect on failure propagation
The second part of the research determines how design architecture affects the propagation of failures throughout an engineered system. System robustness and resistance to topological failure propagation help to describe how a complex engineered system responds to internal and external stimuli.
The cascading failure is modeled as a contact process, introduced by Harris (Reference Harris1974), and has wide applications in engineering and science (Durrett, Reference Durrett1999; Marro & Dickman, Reference Marro and Dickman2005). A typical contact process starts with a component in its failure mode, which affects the neighboring components at a rate that is proportional to the total number of faulty components. For such a system with n components, given any set of initially faulty components, the propagation of failure between components exists in a finite amount of time. This paper presents a reasoning method based on the length of time that the failure propagation is active in the system. With this information, system architectures can be identified that are resilient to the transmission of failures.
Spectral radius has thus far been presented as a quantity capable of producing insights into network resilience to propagating attacks. This metric is based off an evaluation of the network topology as a whole rather than the individual nodes providing avenues for attack propagation. In essence, the spectral radius metric does not capture a network's inherent ability to “bottle-neck” failures with local topology. The following network propagation models allow for this type of analysis.
3.2.1. NLDS modeling
The NLDS propagation model provides an indication for the length of time to full propagation according to the graph layout defined by an adjacency matrix. In the proposed model, a universal failure cascading rate β (0 ≤ β ≤ 1) for each edge connected to a faulty component is defined. The model is based on discrete time steps Δ t, with Δ t → 0. During each time interval, Δt, a faulty component i infects its neighboring components with probability β.
This process can be represented as a Markov chain because the process is treated as a discrete time stochastic process with a finite number of states, in this case 2N. Each state in the Markov chain corresponds to a specific design system configuration of N components, each of which can be in one of the two possible states (nominal or failed), which results in 2N possible configurations. In addition, the Markov property that the state of the system at time t + 1 is dependent only on the state of the system at time t is satisfied in this context.
The proposed solution for solving a full Markov chain is exponential in size. In order to overcome this limitation, it is assumed that the states of the neighbors of any given component are independent of one another. Therefore, the no-linear dynamical system of 2N variables is reduced to one with only N variables for the full Markov chain that can be replaced by Eq. (6). This makes the large design problems solvable with closed-form solutions.
The probability that a component i is failed at time t is defined by Pi (t), and the probability that a component i will not be affected by its neighbors in the next time step is denoted by βi(t). This holds if either of following happens:
1. Each neighbor is in its nominal state.
2. Each neighbor is in its failed state but does not transfer the failure with probability (1 – β).
With the consideration of small time steps (Δt → 0), the possibility of multiple cascades within the same Δt is small and can be ignored.
In the above formula, it is assumed that Pj(t – 1) are independent from one another.
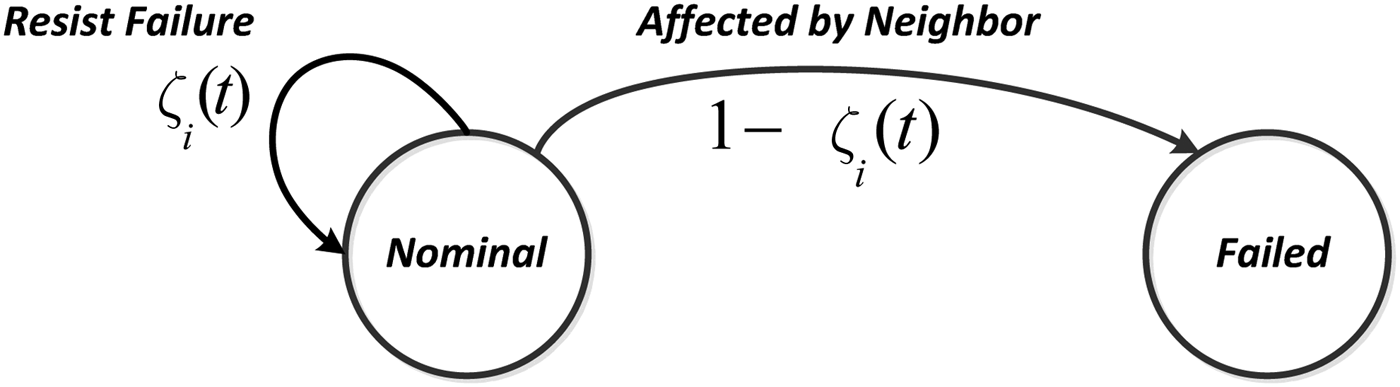
As illustrated in Figure 3, each component at time step t is either nominal or failed. A nominal component i is currently nominal; however, it can be affected (with probability 1 – βi(t)) by one of its faulty neighbors. It is important to note that βi(t) is dependent on the following:
1. The failure birth rate β.
2. The graph topology around component i.

Fig. 3. Transition diagram of the nominal-failed model.
The probability of a component i become faulty at time t is defined by Pi(t):
The above equation can be solved to estimate the time evolution of the number of faulty components ηt, given the specific value of β and a graph topology of the conceptual design, as follows:
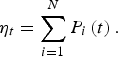 $$\; {{\rm \eta }_t} = \mathop \sum \limits_{i = 1}^N {P_i}\left(t \right).$$
$$\; {{\rm \eta }_t} = \mathop \sum \limits_{i = 1}^N {P_i}\left(t \right).$$3.2.2. Epidemic spreading model
In this approach, the theoretical model is based on the concept that each component in the complex engineered system can exist in a discrete set of states. The failure propagation changes the state of a component from “nominal” to “failure” or from “failure” to “fixed.” As a result, the model is classified as a susceptible–failed–fixed (SFF) model, in which components only exist in one of the three states. The state “fixed” prevents the component from failing by the same cause within the time span of the failure propagation epidemic. The densities of susceptible, failed, and fixed components, S(t), ρ(t), and F(t), respectively, change with time based on the normalization condition, which can be formulated as follows: The proposed methodology is based on the universal rate (μ) in which the failed components are fixed in the design, whereas susceptible components are affected by the failure at a rate (λ) equal to the densities of failed and susceptible components. In addition, ![]() ${\bi \bar K}$ is defined as a number of contacts that each component has with other components per unit time. It is important to note that the assumption made in this proposed model is based on the fact that the propagation of failure is proportional to the density of the faulty components. Therefore, the following differential equations can be defined:
${\bi \bar K}$ is defined as a number of contacts that each component has with other components per unit time. It is important to note that the assumption made in this proposed model is based on the fact that the propagation of failure is proportional to the density of the faulty components. Therefore, the following differential equations can be defined:
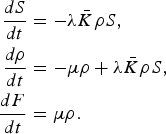 $$\eqalign{\displaystyle{{dS} \over {dt}} &= - {\rm \lambda }\bar K{\rm \rho }S\comma \cr\; \; \; \displaystyle{{d{\rm \rho }} \over {dt}} &= - {\rm \mu} {\rm \rho } + {\rm \lambda}\bar K{\rm \rho}S\comma \; \; \cr\displaystyle{{dF} \over {dt}} &= {\rm \mu} {\rm \rho }.}$$
$$\eqalign{\displaystyle{{dS} \over {dt}} &= - {\rm \lambda }\bar K{\rm \rho }S\comma \cr\; \; \; \displaystyle{{d{\rm \rho }} \over {dt}} &= - {\rm \mu} {\rm \rho } + {\rm \lambda}\bar K{\rm \rho}S\comma \; \; \cr\displaystyle{{dF} \over {dt}} &= {\rm \mu} {\rm \rho }.}$$In order to estimate S(t), the initial conditions of F(0) = 0 (no design fix is implemented yet), S(0) ≅ 1 (almost all the components are in their nominal or susceptible modes), and ρ(0) ≅ 0 (small number of faulty components exist in the initial design) is assumed. Therefore the following can be obtained for
In order to address the contact process in an engineered system, a general connectivity distribution P(k) is defined for each design network. At each time step, each nominal or susceptible component is affected with probability λ, in the case of being connected to one or more faulty components. At the same time, every faulty component is repaired in the system design. It is assumed that the designers of the system fix the faulty components with probability μ. Because every component in an engineered system has different degrees of connectivity (k), the time evolution of ρk(t), Sk(t), and Fk(t), which are the density of faulty, susceptible, and fixed components with connectivity k at time t, is considered and analyzed. Therefore, Eq. (9) can be replaced by the following:
As a result, the global variables such as ρk (t), Sk(t), and Fk(t) are expressed by an average over the different connectivity classes:
The above equations, combined with initial conditions of the system design at t = 0, can be defined and evaluated for any complex engineered system.
4. CASE STUDY
The paper explores the design space for two case studies to demonstrate the features of graph spectral theory on complex engineered system design. The Advanced Diagnostics and Prognostics Testbed (ADAPT) is designed based on the requirement to generate, store, distribute, and monitor electrical power in an exploration vehicle. The electrical power system (EPS) testbed developed at NASA Ames Research Center is used as an example to describe the spectral analysis process, while the ramp system of an infantry fighting vehicle (IFV) is used to provide comparisons between designs.
In addition, two failure propagation models are implemented on the IFV network models in an effort to examine their topological structure for resilience to failure propagation. These models, the NLDS model and the SFF epidemic spreading model, are presented with two cases of different failure origins, a highly connected component (an electrical ground node) and a minimally connected component (an electrical circuit breaker node).
4.1. Graph spectral theory
Spectral graph approaches were utilized on the ADAPT testbed and the IFV ramp networks. This analysis includes an evaluation of network robustness from algebraic connectivity, overall network resilience to propagations from spectral radius, and an evaluation of modularity.
4.1.1. ADAPT EPS
Figure 4 displays the Modelica (Tiller, Reference Tiller2001) representation of an existing design of an EPS (Poll et al., Reference Poll, Patterson, Camisa, Garcia, Hall, Lee, Mengshoel, Neukom, Nishikawa and Ossenfort2007). Modelica is a language for hierarchical object oriented modeling of engineered systems, which was developed through an international effort. The EPS model contains a power source connected through a series of relays to an inverter and several loads consisting of a large fan, a DC resistor, and an AC resistor. A series of four AC or DC voltage sensors and three current transmitters measure the voltage and current at different points throughout the circuit.

Fig. 4. Model of the existing electrical power system design architecture.
The Modelica representation of the system is converted to a network representation as described in Section 3. The generated network is used to convert the system into an adjacency matrix of nodes (components) and edge connections. Including the electrical ground, the EPS system consists of 25 nodes or “components.” These nodes and edges define the connectedness of the system, or the design architecture of the system.
The first step is to create the adjacency matrix of the network representation of the EPS system. The first row depicts the battery and its connections to other components in the system. The first column of the first row is represented by a set of zeros, because the battery is not connected to itself. The second column of the first row is assigned 1, representing the battery's connection to the circuit breaker. Therefore, each row in the matrix represents a component in the design and each column signifies the component's connections with other components in the system. Then the degree matrix and Laplacian matrix for the EPS, which resulted from Eqs. (2) and (3), are created. A table of the eigenvalues resulting from the adjacency matrix and the Laplacian matrix can be found as Table 1. From the eigenvalues of the adjacency matrix, a spectral radius of 3.324 is computed. As stated previously, this number is not directly usable without a comparison to other designs. However, because this example is meant to show the process of converting a complex engineered system model to a network, the implications of the spectral radius will be discussed further with the comparison of the ramp models.
Table 1. Eigenvalues generated in EPS design architecture

As seen from Table 2, nearly half of the components within the EPS system are also modules. Because many electrical components can only be connected in certain configurations, the possible system design space is limited. The analyzed EPS has components connected in both series and parallel connections, with the parallel connections representing electrical modules. Alternatively, the algebraic connectivity of the system is rather high when compared to the ramp designs, as discussed in the next section. This is mainly due to the properties of an electrical circuit. The EPS is modeled with a ground as a component within the system graph. An electrical ground must exist and be connected to the proper components in order to complete the circuit. As a result, circuits tend to be interconnected, which increases the average node degree of the graph and the algebraic connectivity. However, this relationship does not always apply. As will be seen in a ramp design case study, a high average node degree does not always correspond directly to an increased algebraic connectivity. Some systems contain subsystems, which are independent of the overall system but highly interconnected within their own subsystems (high average node degree). Therefore, if the rest of the system is sparsely connected, the isolated area of high interconnectedness drives the average node degree of the system up, while the algebraic connectivity remains low because it relates to the Laplacian of the overall system.
Table 2. Spec EPS design architecture

4.1.2. Ramp system of the IFV
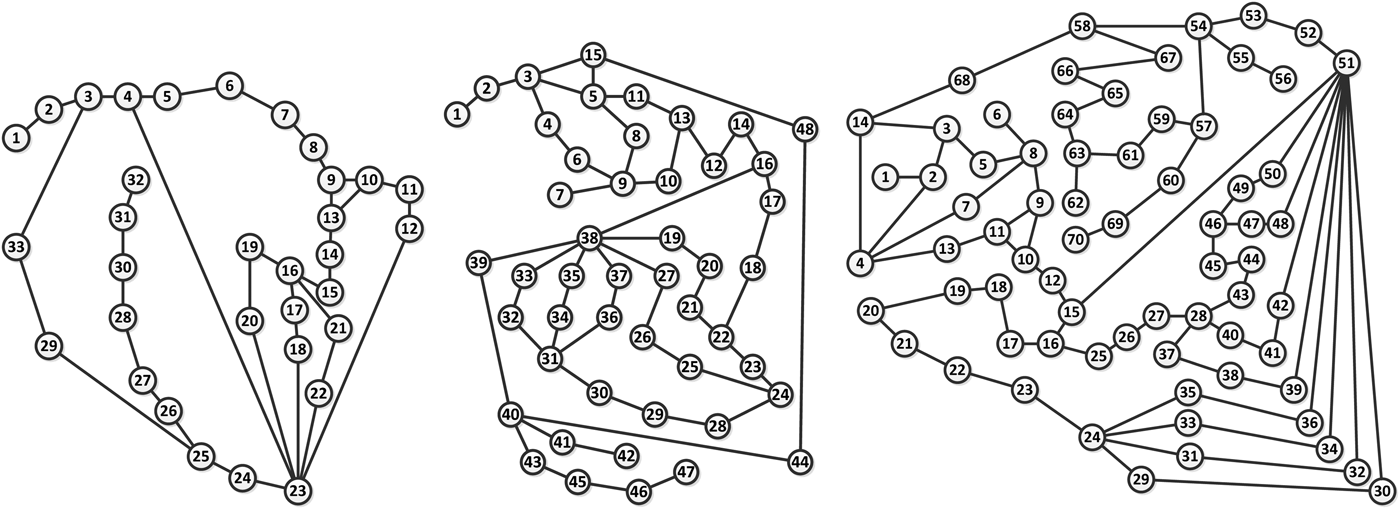
To demonstrate the benefits and scalability of using spectral graph theory on complex engineered systems, a ramp system of the IFV is modeled and analyzed next. The modeled ramp is located at the rear of the IFV and used for the speedy exit and entry of the troops, and the power-operated ramp is also fitted with a door. A hierarchical Modelica ramp model consists of an EPS (Fig. 4), a mechanical ramp subsystem, a controller subsystem, and a crew subsystem.
Graph spectral analysis was conducted on three different design architectures of the ramp system. Figures 5, 6, and 7 illustrate the design options. Each design implemented in Modelica is a system of subsystems. Therefore, every “component” seen in the designs is actually a system of components making up a larger nodal percentage of the system as a whole. Each design consists of at least a unique EPS and a mechanical subsystem. In addition, each design has modeled troops entering, exiting, and residing within the vehicle.

Fig. 5. Ramp design architecture #1.

Fig. 6. Ramp design architecture #2.

Fig. 7. Ramp design architecture #3.
The graph representations of the three ramp designs are shown displayed in Figure 8. In addition, Table 3 provides pertinent information concerning the three designs for use with both propagation models. Included is the design identification number to be used during the analysis, the number of nodes (components) contained within each design, the minimum degree, the maximum degree, the average degree, and the number of modules.

Fig. 8. Graph representation of ramp designs #1, #2, and #3.
Table 3. Spec ramp design architectures

Each ramp design is analyzed for failure propagation by evaluating the design architecture for the length of time to full propagation (NLDS) and for the breadth of propagation (SFF) when a failure is introduced. The third ramp design consists of the highest number of modules, yet has the lowest algebraic connectivity. This is an important insight, because it is commonly known that modularity in complex engineered systems is useful for system construction and maintainability, but the isolation of failures into a single module typically makes the system less robust, as shown.
4.2. Failure propagation models
Two failure propagation models are used to explore the design space of the ramp system of an IFV to demonstrate resilience against cascading failure. Three complete ramp system designs will be assessed with a NLDS and an epidemic spreading model.
Table 4 provides the information for failure origin utilized in this simulation. Node numbers have been provided that correlate to the node numbers used in Figure 8.
Table 4. Initial faulty components in the ramp designs

4.2.1. NLDS
In order to gauge the degree of failure propagation in the design architectures (Fig. 9), an initial set of components in a state of failure is defined so the failure can propagate along the underlying graph structure of the architecture. For the sake of comparison, each topology has been compared twice, once with an initially failed, minimally connected component and once with a highly connected component. In addition, in order to compare different architectures, each cascade is set to originate from the internal EPS subsystem, or the EPS of each conceptual design. Specifically, a minimally connected circuit breaker and a highly connected ground terminal are selected as the failure origins.

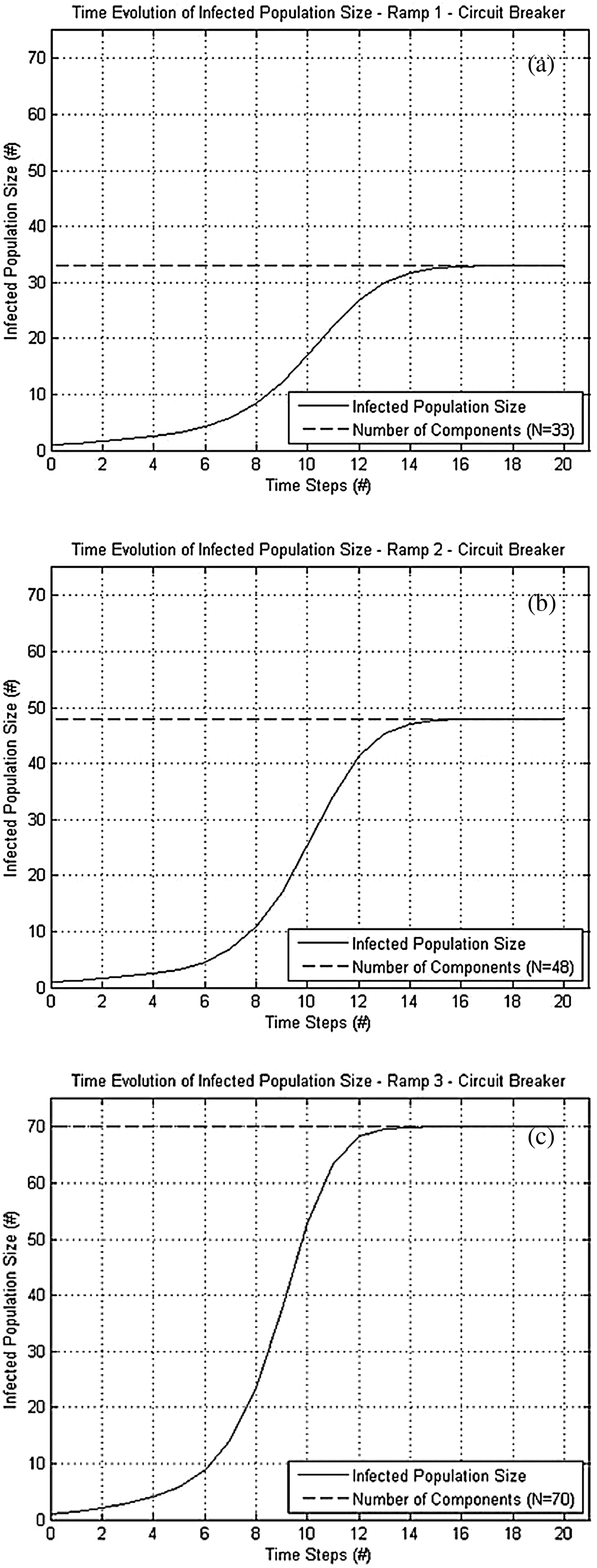
Fig. 9. Time evolution of faulty components' population size in ramp design (a) #1, (b) #2, and (c) #3 (origin of failure: circuit breaker).
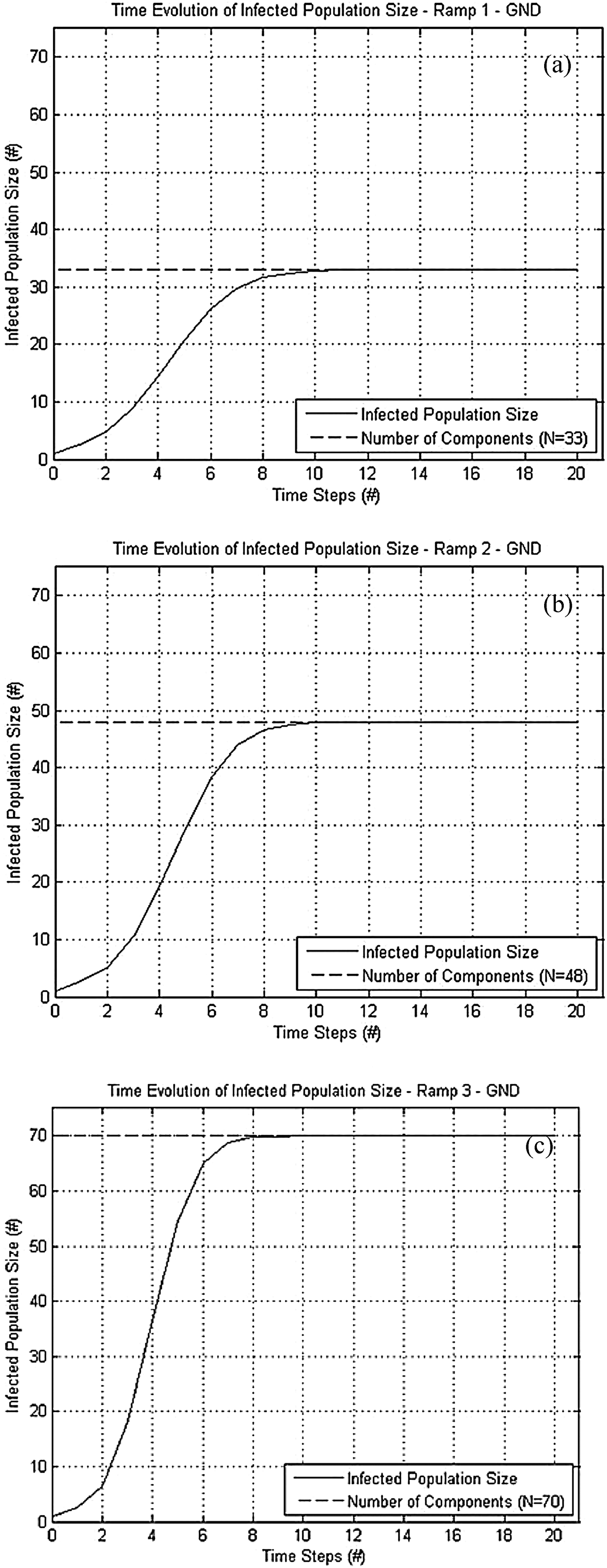
As can be seen in Figure 9 the population of the infected components with respect to time is the same for all three different design ramps. In the EPS subsystem of each ramp design, the circuit breaker has two connected components that can be infected. Therefore, all three designs propagate similarly until a component is failed, which can cause a drastic increase in infected population size. This occurred near the sixth time step for each design. For instance, when the failure reaches the ground node of the EPS, the failure is able to spread much more quickly because the ground node is the most highly connected component in each design. The result confirms the expectation that a more highly connected component propagates failure to neighboring component more quickly, while a minimally connected component, such as a circuit breaker, results in slower failure propagation. As can be directly observed from Figure 10, a failure originating from a more highly connected component (in this case the EPS ground) propagates much more rapidly.

Fig. 10. Time evolution of faulty components' population size in ramp design (a) #1, (b) #2, and (c) #3 (origin of failure: ground).
The NLDS model proves that more highly connected components spread a failure much faster. Therefore, nodal hubs, or very modular areas of a design, are more detrimental to the rapid spread of a failure. However, simply having modular design structures does not suggest an inadequacy in resilience toward failure cascades. As can be seen from Table 3, a large percentage of the components within each design are considered modular hubs.
An important design aspect to note, however, is that there was no significant evidence for either initial failure state to suggest that one ramp design was more resilient to failure cascades than any others. This is based on the assumption that cascading time defines resilience and not infected population size. When the same, minimally connected circuit breaker has failed in each design, the time to full propagation for each design is approximately 14 time steps. When the ground terminal is initially failed, the time to full propagation is approximately 8 time steps. In addition, the shape of each relationship, representing the progression of failed population size, does not indicate any design being more resilient to failure propagations.
4.2.2. SFF
Unlike the NLDS model, the SFF epidemic spreading model is based on the idea that failure propagation can be stopped by fixing the faulty components. The SFF model operates by the spread of a failure from an initially failed component just as the NLDS model does. However, the SFF model is not a probabilistic model that is solely dependent on the architecture of an adjacency matrix as the NLDS model is. Instead, the SFF model requires a time step dependent simulation of the spread of a component failure. As with the NLDS model, a time step is regarded as sufficiently close to zero so that only the current population of failed components transmit a failure.
Each “faulty” component has an opportunity to infect a neighboring susceptible component in the next time step. In one time step, a component infects its connected neighbors according to a uniform failure probability. The simulation run for the SFF model was conducted at λ = 10%. After a component has had an opportunity to infect its neighbors, the infected component would then be fixed in the conceptual design to resist the same failure according to the probability of failure removal μ = 10%. A repaired component is either considered faulty without the ability to transfer the failure to the neighboring components or is susceptible but resistant to the failures of its connected neighbors. Therefore, the cascading failure could be stopped with the provision that enough faulty components become repaired in the design before they are able to fully propagate the failure; that is, propagations can be halted if all transmission routes are blocked by repaired components.
The same designs were used with the SFF as were used with the NLDS model. In addition, the same initial failure conditions were used. An EPS circuit breaker was initially failed as a minimally connected component. A ground node was then initially used to propagate the failure as a highly connected component. Figure 11 shows the epidemic spreading graphs for an initially failed circuit breaker within the EPS for each ramp design.

Fig. 11. Time evolution of faulty components density for ramp designs (a) #1, (b) #2, and (c) #3 (origin of failure: circuit breaker). The k value is the indicative of the degree of the components followed by the number of components within that data set.
In order to compare the time evolution of faulty component density in the three different conceptual ramp designs, a component with an equal number of connections from the EPS subsystems of the ramps is chosen as an initial faulty component. The reason for this is because SFF failure propagation is based on connections; therefore, the results must be reported in terms of faulty component density. As is depicted in Figure 11, each data set is representative of a set of components with the same degree (e.g., ramp #1: red colored data set represents six components in the system design with only three connections). Therefore, each set of components has a failure density ranging from 0 to 1; 0 means that no components of that degree are infected, and 1 means that every component of that degree is infected. Fixed components are not considered faulty. Consequently, a plot of faulty component density fluctuates intermittently between 0 and 1, but it eventually settles at 0 as all failed components are fixed in the system design. In the legend of each graph, a k value is given, which is indicative of the degree of the components followed by the number of components within that data set. When a minimally connected component, such as a circuit breaker, is chosen as a failure origin, it is compared to an initially infected highly connected component, such as a ground, and the failure spreads more slowly, as expected.
Figure 12 illustrates the simulation results for an initially failed, highly connected ground terminal. The plots present more immediate increases in infection density, regardless of component degree when a highly connected component is failed initially. However, once the initial infection has passed and the failure density begins to subside, the reduction of infection density is not dependent on architecture. This is because a stopped failure is repaired according to a uniform probability. This failure is not then passed between connected components.

Fig. 12. Time evolution of faulty components density for ramp design (a) #1, (b) #2, and (c) #3 (origin of failure: ground).
5. DISCUSSION
The first ramp design consisted of the fewest number of components. Each ramp design was highly modular, especially the third design, which is the most modular EPS. The third ramp design is a good example of why looking at the average node degree and algebraic connectivity independently is an unreliable exercise. As can be seen from the results in Table 2, the first two ramp designs are very similar. This is not the case with the third ramp design, which has a smaller algebraic connectivity with more modules. This is due to the third EPS design used with that ramp variant. When compared to the other two EPS designs, the third design has an algebraic connectivity half that of the other two. In addition, the third EPS design has more components than the others with a similar average node degree. However, the maximum node degree of the third design was greater than the other EPS variants. Upon further examination, the third EPS design is found to have many components that are only connected to two components, one that supplies electrical current and one that receives current, making it simpler to make a component independent from the rest of the system. In addition, a limited number of components are connected to many others. This small number of components is what drives the average node degree of the system up, making each EPS design appear similar by average node degree. However, because the algebraic connectivity is a measure of the difficulty in making a component independent of the rest of the system, the algebraic connectivity of the third ramp design remains low because of the number of components that have a fewer number of connections. The low algebraic connectivity is consistent with the recommendation for modular physical system architectures that may have the unintended downside of making the systems less tolerant to failure.
After both models were applied to each of the three ramp designs, the NLDS model did not show any relevant evidence to suggest that any one ramp design (graph layout) was more resilient to propagations than the others. However, conclusions can still be drawn from the results and are discussed below. The length of time to full propagation was not significantly different between designs. The NLDS model can adequately identify those design components that are critical to a system and whose failure would cause shutdown of the whole system, as can be seen by the differences in failure origins. Conversely, the SFF model can be used to compare different conceptual design architectures for resilience to propagation. This can be done by analyzing how a failure propagates through a system and then fixing failed components to inhibit the propagation of the failure. The SFF model determined that the third ramp design was more resilient to specific nodal attacks, because both simulations indicated a similar infection breadth. This result is consistent with the observation of spectral analysis, because the third design is more modular compared to the other designs. Therefore, it has a high robustness only because the failure of components can be isolated to its module.
A couple of telling conclusions can be drawn from the result of the case study. First, the NLDS models showed that connectivity plays a major role in how fast an epidemic spreads. A few components with a higher degree increase the speed of infection throughout a system. This was conclusively shown because the third ramp design, having a few nodes with a higher degree than the other designs, will propagate a failure faster. Second, larger systems will lessen the impact of random or targeted attacks. The ramp system designs showed this because the normalized percentage of failure began to equalize between components with fewer connections and components with more connections that were used as failure origins when the system size increased. Both conclusions provide insight into design architectures that can be more resilient to failures.
6. CONCLUSIONS AND FUTURE WORK
Establishing robustness during the conceptual design phase is a difficult yet important aspect to the design of engineered systems. Utilizing complex network theory in conjunction with spectral analysis has provided useful insight into the design of robust complex engineering systems. Spectral analysis provides valuable metrics in quantifying certain aspects of complex networks. These metrics are algebraic connectivity, modularity, and spectral radius. As stated in this paper, the algebraic connectivity represents the difficulty in making one node independent of the rest of the system. A higher algebraic connectivity denotes an increase in components' connectivity and higher robustness of the overall system. Because of the close correlation between complex networks and complex engineered systems, algebraic connectivity is a good metric to be considered to determine the resilience of the architecture of complex systems.
To determine the resiliency characteristics of complex engineered systems, two case studies involving complex engineered systems were analyzed using spectral analysis. Utilizing the algebraic connectivity as the main analysis metric, both case studies provided evidence for the validity of using graph spectral theory on complex engineered systems.
Further, in the second part of the research based on the two propagation models, a NLDS model and an SFF epidemic spreading model are developed for use during the early design of complex systems. From the two models, equations are provided to model the propagation characteristics of failures in complex engineered systems. The NLDS propagation model provides an indication for the length of time to full propagation according to a graph layout. The SFF epidemic spreading model provides an indication of the extent of a cascade according to a graph layout.
Although both models provide an indication into properties relating to failure propagation, they both require the accurate modeling of a complex engineered system as a graph. This is no trivial task. Because the graph of a system is dependent on how connections are defined, it becomes increasingly important to develop a standard methodology for modeling. In this paper, the ramp designs were modeled based on physical connectivity. To more accurately analyze these propagations, additional research would analyze the effect on a complex engineered system if its graph were created using different, and perhaps more complicated, metrics of design dependency. Such justifications could include expanded physical connections that are inclusive of secondary component interactions. They do not necessarily have a physical connection interface and may be produced as a consequence of system operation. This could include heat, noise, and vibration related interactions, among others. In addition, justifications related to EMS flows would be a necessary next addition to analyze these models for applicability with complex engineered systems. EMS flow relations would create connections between components that share a flow. For instance, two components would be connected as a part of a thermodynamic process if the same working fluid travels from one component to the other.
Analyzing multiple adjacency matrices created with various connection justifications per design would provide a more complete look at a design's resilience to propagations. This would add computational expense in the analysis of the design and designer effort to create the matrices. An automated method to create the adjacency matrices would solve this issue; however, this would require an interface between a design tool such as a computer-aided design suite and a matrix creator.
In order to validate the use of these models, performance data of an engineered system that is operating in a state of failure is a necessary next step. By analyzing the time-dependent response of a system under failure, the propagation properties predicted by these models can be verified.
Christopher Hoyle is currently an Assistant Professor and Arthur Hitsman Faculty Scholar in design in the Mechanical Engineering Department at Oregon State University. He received his PhD from Northwestern University in Mechanical Engineering in 2009 and his master's degree in mechanical engineering from Purdue University in 1994. He was previously a Design Engineer and an Engineering Manager at Motorola, Inc., for 10 years before enrolling in the PhD program. His current research interests are focused upon decision making in engineering design, with emphasis on the early design phase. His research contributions are to the field of decision-based design, specifically in linking consumer preferences and enterprise-level objectives with the engineering design process. His areas of expertise are uncertainty propagation methodologies, Bayesian statistics and modeling, stochastic consumer choice modeling, optimization, and design automation. He is coauthor of the book Decision-Based Design: Integrating Consumer Preferences into Engineering Design.
Hoda Mehrpouyan is a PhD candidate in mechanical engineering in the Complex Engineered Systems Design Laboratory at Oregon State University. She received her MS degree in software engineering and management from Linköping University in 2011. She spent 7 years in industry as a System Delivery Consultant and Programmer Analyst prior to returning to academia. Her research focuses on model-based systems engineering, resilience and safety analysis, information technology, and simulation and verification to support the design of complex systems.
Brandon Haley is a Research Assistant in design in the Mechanical Engineering Department at Oregon State University, from which he received his master's degree in 2014. His current research interests are focused on developing evaluations of reliability and robustness for complex engineered systems. Specifically, the research is heavily focused during the early stages of design when risk and cost related to design changes are low. In addition, risk mitigation techniques and the evaluation of failures are of high interest considering that reliability analyses are typically highly dependent on system performance both inside and outside of failure states.
Irem Y. Tumer is a Professor of mechanical, industrial, and manufacturing engineering at Oregon State University, where she leads the Complex Engineered System Design Laboratory, and Associate Dean for Research and Economic Development for the College of Engineering. Prior to accepting a faculty position at Oregon State University, Dr. Tumer led the Complex Systems Design and Engineering group in the Intelligent Systems Division at NASA Ames Research Center, where she worked from 1998 through 2006 as Research Scientist, Group Lead, and Program Manager. She received her PhD in mechanical engineering from the University of Texas at Austin in 1998. Since moving to Oregon State University in 2006, her funding has largely been through NSF, AFOSR, DARPA, and NASA. Dr. Tumer was Conference Chair for ASMEs Design for Manufacturing and the Lifecycle Conference in 2000, Program Chair for IEEE Reliability Society's Prognostics and Health Management Conference in 2008, and Program Chair (2011) and Conference Chair (2012) for ASMEs International Design Theory and Methodology Conference. She is currently an Associate Editor for the ASME Journal of Mechanical Design and the International Journal of Prognostics and Health Management. Her research focuses on the overall problem of designing highly complex and integrated engineering systems with reduced risk of failures, and developing formal methodologies and approaches for complex system design and analysis.
Andy Dong is the Warren Centre Chair for Engineering Innovation and is on the Faculty of Engineering and Information Technologies at the University of Sydney. He completed his PhD and postdoctoral training in mechanical engineering at the University of California, Berkeley. Dr. Dong was initially a Lecturer on the Faculty of Architecture, Design, and Planning and eventually became the Head of Discipline for the Design Lab. In 2010 he was awarded an Australian Research Council Future Fellowship. He is on the editorial board of Design Studies, the Journal of Engineering Design, and Research in Engineering Design. Dr. Dong's research addresses the central activity of engineering: the design of new products and services.