Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-26T05:26:11.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Superstable manifolds of invariant circles and codimension-one Böttcher functions

Published online by Cambridge University Press:  05 July 2013

SCOTT R. KASCHNER  and
ROLAND K. W. ROEDER
SCOTT R. KASCHNER
Affiliation:
IUPUI Department of Mathematical Sciences, LD Building, Room 270, 402 North Blackford Street, Indianapolis, Indiana 46202-3267, USA email srkaschn@iupui.edurroeder@math.iupui.edu
ROLAND K. W. ROEDER
Affiliation:
IUPUI Department of Mathematical Sciences, LD Building, Room 270, 402 North Blackford Street, Indianapolis, Indiana 46202-3267, USA email srkaschn@iupui.edurroeder@math.iupui.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 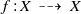$f: X~\dashrightarrow ~X$ be a dominant meromorphic self-map, where 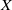$X$ is a compact, connected complex manifold of dimension 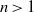$n\gt 1$. Suppose that there is an embedded copy of 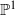${ \mathbb{P} }^{1} $ that is invariant under 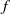$f$, with 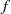$f$ holomorphic and transversally superattracting with degree $a$ in some neighborhood. Suppose that 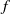$f$ restricted to this line is given by 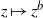$z\mapsto {z}^{b} $, with resulting invariant circle 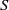$S$. We prove that if 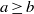$a\geq b$, then the local stable manifold 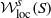${ \mathcal{W} }_{\mathrm{loc} }^{s} (S)$ is real analytic. In fact, we state and prove a suitable localized version that can be useful in wider contexts. We then show that the condition 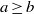$a\geq b$ cannot be relaxed without adding additional hypotheses by presenting two examples with 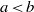$a\lt b$ for which 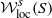${ \mathcal{W} }_{\mathrm{loc} }^{s} (S)$ is not real analytic in the neighborhood of any point.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 1 , February 2015 , pp. 152 - 175
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baouendi, M. S. and Rothschild, L. P.. Images of real hypersurfaces under holomorphic mappings. J. Differential Geom. 36 (1) (1992), 75–88.Google Scholar
Bedford, E. and Jonsson, M.. Dynamics of regular polynomial endomorphisms of ${\mathbf{C} }^{k} $. Amer. J. Math. 122 (1) (2000), 153–212.CrossRefGoogle Scholar
Bedford, E. and Jonsson, M.. Potential theory in complex dynamics: regular polynomial mappings of ${\mathbf{C} }^{k} $. Complex Analysis and Geometry (Paris, 1997) (Progress in Mathematics, 188). Birkhäuser, Basel, 2000, pp. 203–211.CrossRefGoogle Scholar
Bleher, P. M. and Žalys, E.. Asymptotics of the susceptibility for the Ising model on the hierarchical lattices. Comm. Math. Phys. 120 (3) (1989), 409–436.Google Scholar
Bleher, P., Lyubich, M. and Roeder, R.. Lee-Yang zeros for DHL and 2D rational dynamics, I. Foliation of the physical cylinder. Preprint, http://arxiv.org/abs/1009.4691.Google Scholar
Bleher, P., Lyubich, M. and Roeder, R.. Lee–Yang–Fisher zeros for DHL and 2D rational dynamics, II. Global pluripotential interpretation. Preprint, http://arxiv.org/abs/1107.5764.Google Scholar
Böttcher, L. E.. The principal laws of convergence of iterates and their application to analysis (Russian). Izv. Kazan. Fiz.-Mat. Obshch. 14 (1904), 155–234.Google Scholar
Buff, X., Epstein, A. and Koch, S.. Böttcher coordinates. Preprint, http://arxiv.org/abs/1104.2981.Google Scholar
Domoradzki, S. and Stawiska, M.. Lucjan Emil Böttcher and his mathematical legacy. Preprint, http://arxiv.org/abs/1207.2747.Google Scholar
Favre, C. and Jonsson, M.. Eigenvaluations. Ann. Sci. Éc. Norm. Supér. (4) 40 (2007), 309–349.Google Scholar
Fornæss, J. E. and Sibony, N.. Hyperbolic maps on ${ \mathbb{P} }^{2} $. Math. Ann. 311 (2) (1998), 305–333.Google Scholar
Gignac, W.. On the growth of local intersection multiplicities in holomorphic dynamics: a conjecture of Arnold. Preprint, http://arxiv.org/abs/1212.5272.Google Scholar
Gignac, W. and Ruggiero, M.. Growth of attraction rates for iterates of a superattracting germ in dimension two. Preprint, http://arxiv.org/abs/1209.3450.Google Scholar
Hirsch, M. W., Pugh, C. C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583). Springer, Berlin, 1977.Google Scholar
Hruska, S. L. and Roeder, R. K. W.. Topology of Fatou components for endomorphisms of $ \mathbb{C} { \mathbb{P} }^{k} $: linking with the Green’s current. Fund. Math. 210 (1) (2010), 73–98.Google Scholar
Hubbard, J. H. and Papadopol, P.. Superattracting fixed points in ${ \mathbb{C} }^{n} $. Indiana Univ. Math. J. 433 (1994), 21–365.Google Scholar
Isakov, S. N.. Nonanalytic features of the first order phase transition in the Ising model. Comm. Math. Phys. 95 (4) (1984), 427–443.Google Scholar
Jonsson, M.. Dynamical studies in several complex variables. PhD Thesis, Royal Institute of Technology, 1997.Google Scholar
Krantz, S. G.. Function Theory of Several Complex Variables. AMS Chelsea Publishing, Providence, RI, 2001, reprint of the 1992 edition.Google Scholar
Lee, T. D. and Yang, C. N.. Statistical theory of equations of state and phase transitions. II. Lattice gas and Ising model. Phys. Rev. (2) 87 (1952), 410–419.Google Scholar
Lyubich, M. Y.. Some typical properties of the dynamics of rational mappings. Uspekhi Mat. Nauk 38 (5(233)) (1983), 197–198.Google Scholar
Mañé, R., Sad, P. and Sullivan, D.. On the dynamics of rational maps. Ann. Sci. Éc. Norm. Supér (4) 16 (2) (1983), 193–217.Google Scholar
Milnor, J.. Dynamics in One Complex Variable (Annals of Mathematics Studies, 160), 3rd edn. Princeton University Press, Princeton, NJ, 2006.Google Scholar
Nishino, T.. Function Theory in Several Complex Variables (Translations of Mathematical Monographs, 193). American Mathematical Society, Providence, RI, 2001, Translated from the 1996 Japanese original by N. Levenberg and H. Yamaguchi.Google Scholar
Palis, J., de Melo, W. and Manning, A. K.. Geometric Theory of Dynamical Systems. Springer, New York, 1982.Google Scholar
Peng, G.. On the dynamics of nondegenerate polynomial endomorphisms of ${\mathbf{C} }^{2} $. J. Math. Anal. Appl. (2) 237 (1999), 609–621.CrossRefGoogle Scholar
Pugh, C. and Shub, M.. Ergodic attractors. Trans. Amer. Math. Soc. 312 (1) (1989), 1–54.Google Scholar
Pujals, E. R. and Roeder, R. K. W.. Two-dimensional Blaschke products: degree growth and ergodic consequences. Indiana Univ. Math. J. 59 (2010), 301–326.Google Scholar
Rea, C.. Levi-flat submanifolds and holomorphic extension of foliations. Ann. Sc. Norm. Super. Pisa Cl. Sci. (3) 26 (1972), 665–681.Google Scholar
Roeder, R. K. W.. A degenerate Newton’s map in two complex variables: linking with currents. J. Geom. Anal. (17) 1 (2007), 107–146.Google Scholar
Ruggiero, M.. Rigidification of holomorphic germs with noninvertible differential. Michigan Math. J. (1) 61 (2012), 161–185.Google Scholar
Ueda, T.. Complex Dynamical Systems on Projective Spaces (Proc. RIMS Conference on Chaotic Dynamical Systems, 7–10 July 1992) (Advanced Series in Dynamical Systems, 13). Ed. Ushiki, S.. World Scientific, Singapore, 1993, pp. 120–138.Google Scholar
Ushiki, S.. Böttcher’s Theorem and Super-stable Manifolds for Multidimensional Complex Dynamical Systems (Proc. RIMS Conference on Chaotic Dynamical Systems, Kyoto, 18–21 February 1991) (Advanced Series in Dynamical Systems, 11). Ed. Ushiki, S.. World Scientific, Singapore, 1992, pp. 168–184.Google Scholar
Ushiki, S.. Super-stable Manifolds of Super-saddle-type Julia Sets in C2 (Proc. RIMS Conference on Chaotic Dynamical Systems, 7–10 July 1992) (Advanced Series in Dynamical Systems, 13). Ed. Ushiki, S.. World Scientific, Singapore, 1993, pp. 165–180.Google Scholar
Yang, C. N. and Lee, T. D.. Statistical theory of equations of state and phase transitions. I. Theory of condensation. Phys. Rev. (2) 87 (1952), 404–409.Google Scholar