Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-26T01:15:44.981Z Has data issue: false hasContentIssue false
  • English
  • Français

Toroidal and poloidal energy in rotating Rayleigh–Bénard convection

Published online by Cambridge University Press:  02 December 2014

Susanne Horn  and
Olga Shishkina
Susanne Horn*
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, Am Faßberg 17, 37077 Göttingen, Germany Institute of Aerodynamics and Flow Technology, German Aerospace Center (DLR), Bunsenstraße 10, 37073 Göttingen, Germany
Olga Shishkina
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, Am Faßberg 17, 37077 Göttingen, Germany Institute of Aerodynamics and Flow Technology, German Aerospace Center (DLR), Bunsenstraße 10, 37073 Göttingen, Germany
*
†Present address: Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK. Email address for correspondence: s.horn@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

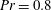We consider rotating Rayleigh–Bénard convection of a fluid with a Prandtl number of $\mathit{Pr}=0.8$ in a cylindrical cell with an aspect ratio 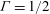${\it\Gamma}=1/2$. Direct numerical simulations (DNS) were performed for the Rayleigh number range 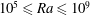$10^{5}\leqslant \mathit{Ra}\leqslant 10^{9}$ and the inverse Rossby number range 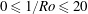$0\leqslant 1/\mathit{Ro}\leqslant 20$. We propose a method to capture regime transitions based on the decomposition of the velocity field into toroidal and poloidal parts. We identify four different regimes. First, a buoyancy-dominated regime occurring while the toroidal energy 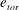$e_{tor}$ is not affected by rotation and remains equal to that in the non-rotating case, 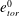$e_{tor}^{0}$. Second, a rotation-influenced regime, starting at rotation rates where 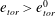$e_{tor}>e_{tor}^{0}$ and ending at a critical inverse Rossby number 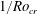$1/\mathit{Ro}_{cr}$ that is determined by the balance of the toroidal and poloidal energy, 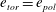$e_{tor}=e_{pol}$. Third, a rotation-dominated regime, where the toroidal energy 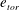$e_{tor}$ is larger than both 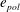$e_{pol}$ and 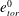$e_{tor}^{0}$. Fourth, a geostrophic regime for high rotation rates where the toroidal energy drops below the value for non-rotating convection.

JFM classification

Geophysical and Geological Flows: Rotating flows Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 762 , 10 January 2015 , pp. 232 - 255
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., He, X., Funfschilling, D. & Bodenschatz, E. 2012 Heat transport by turbulent Rayleigh–Bénard convection for $\mathit{Pr}\simeq 0.8$ and $3\times 10^{12}\lesssim \mathit{Ra}\lesssim 10^{15}$ : aspect ratio ${\it\Gamma}=0.50$ . New J. Phys. 14 (10), 103012.Google Scholar
Backus, G. 1986 Poloidal and toroidal fields in geomagnetic field modeling. Rev. Geophys. 24 (1), 75–109.Google Scholar
Boronski, P. & Tuckerman, L. S. 2007 Poloidal–toroidal decomposition in a finite cylinder. I: influence matrices for the magnetohydrodynamic equations. J. Comput. Phys. 227 (2), 1523–1543.CrossRefGoogle Scholar
Breuer, M., Wessling, S., Schmalzl, J. & Hansen, U. 2004 Effect of inertia in Rayleigh–Bénard convection. Phys. Rev. E 69 (2), 26302.Google Scholar
Buell, J. C. & Catton, I. 1983 Effect of rotation on the stability of a bounded cylindrical layer of fluid heated from below. Phys. Fluids 26, 892–896.CrossRefGoogle Scholar
Busse, F. H. 1967 On the stability of two-dimensional convection in a layer heated from below. J. Math. Phys. 46, 140–150.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon.Google Scholar
Ecke, R. E. & Niemela, J. J. 2014 Heat transport in the geostrophic regime of rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 113, 114301.Google Scholar
Ecke, R. E., Zhong, F. & Knobloch, E. 1992 Hopf bifurcation with broken reflection symmetry in rotating Rayleigh–Bénard convection. Europhys. Lett. 19 (3), 177–182.CrossRefGoogle Scholar
Goldstein, H. F., Knobloch, E., Mercader, I. & Net, M. 1993 Convection in a rotating cylinder. Part 1. Linear theory for moderate Prandtl numbers. J. Fluid Mech. 248, 583–604.Google Scholar
Goldstein, H. F., Knobloch, E., Mercader, I. & Net, M. 1994 Convection in a rotating cylinder. Part 2. Linear theory for low Prandtl numbers. J. Fluid Mech. 262, 293–324.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
Hartlep, T., Tilgner, A. & Busse, F. H. 2003 Large scale structures in Rayleigh–Bénard convection at high Rayleigh numbers. Phys. Rev. Lett. 91 (6), 064501.CrossRefGoogle ScholarPubMed
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.CrossRefGoogle Scholar
Herrmann, J. & Busse, F. H. 1993 Asymptotic theory of wall-attached convection in a rotating fluid layer. J. Fluid Mech. 255, 183–194.CrossRefGoogle Scholar
Horn, S. & Shishkina, O. 2014 Rotating non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. Phys. Fluids 26 (5), 055111.CrossRefGoogle Scholar
Horn, S., Shishkina, O. & Wagner, C. 2011 The influence of non-Oberbeck–Boussinesq effects on rotating turbulent Rayleigh–Bénard convection. J. Phys.: Conf. Ser. 318 (8), 082005.Google Scholar
Horn, S., Shishkina, O. & Wagner, C. 2013 On non-Oberbeck–Boussinesq effects in three-dimensional Rayleigh–Bénard convection in glycerol. J. Fluid Mech. 724, 175–202.Google Scholar
Julien, K., Knobloch, E., Rubio, A. M. & Vasil, G. M. 2012 Heat transport in low-Rossby-number Rayleigh–Bénard convection. Phys. Rev. Lett. 109 (25), 254503.CrossRefGoogle ScholarPubMed
Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996 Rapidly rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 322, 243–273.Google Scholar
King, E. M., Stellmach, S. & Aurnou, J. M. 2012 Heat transfer by rapidly rotating Rayleigh–Bénard convection. J. Fluid Mech. 691, 568–582.Google Scholar
King, E. M., Stellmach, S., Noir, J., Hansen, U. & Aurnou, J. M. 2009 Boundary layer control of rotating convection systems. Nature 457, 301–304.Google Scholar
Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2006 Heat flux intensification by vortical flow localization in rotating convection. Phys. Rev. E 74 (5), 056306.Google Scholar
Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2008 Breakdown of large-scale circulation in turbulent rotating convection. Europhys. Lett. 84 (2), 24001.CrossRefGoogle Scholar
Kunnen, R. P. J., Clercx, H. J. H. & van Heijst, G. J. F. 2013 The structure of sidewall boundary layers in confined rotating Rayleigh–Bénard convection. J. Fluid Mech. 727, 509–532.Google Scholar
Kunnen, R. P. J., Geurts, B. J. & Clercx, H. J. H. 2009 Turbulence statistics and energy budget in rotating Rayleigh–Bénard convection. Eur. J. Mech. (B/Fluids) 28 (4), 578–589.CrossRefGoogle Scholar
Kunnen, R. P. J., Geurts, B. J. & Clercx, H. J. H. 2010 Experimental and numerical investigation of turbulent convection in a rotating cylinder. J. Fluid Mech. 626, 445–476.Google Scholar
Kunnen, R. P. J., Stevens, R. J. A. M., Overkamp, J., Sun, C., van Heijst, G. F. & Clercx, H. J. H. 2011 The role of Stewartson and Ekman layers in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 422–442.CrossRefGoogle Scholar
Kuo, E. Y. & Cross, M. C. 1993 Traveling-wave wall states in rotating Rayleigh–Bénard convection. Phys. Rev. E 47 (4), R2245–R2248.CrossRefGoogle ScholarPubMed
Liu, Y. & Ecke, R. E. 2009 Heat transport measurements in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 80 (3), 036314.CrossRefGoogle ScholarPubMed
Marques, F., Net, M., Massaguer, J. M. & Mercader, I. 1993 Thermal convection in vertical cylinders. A method based on potentials of velocity. Comput. Meth. Appl. Mech. Engng 110 (1), 157–169.Google Scholar
Olson, P. & Bercovici, D. 1991 On the equipartition of kinetic energy in plate tectonics. Geophys. Res. Lett. 18 (9), 1751–1754.Google Scholar
Oresta, P., Stringano, G. & Verzicco, R. 2007 Transitional regimes and rotation effects in Rayleigh–Bénard convection in a slender cylindrical cell. Eur. J. Mech. (B/Fluids) 26 (1), 1–14.CrossRefGoogle Scholar
Ostilla-Mónico, R., van der Poel, E. P., Kunnen, R. P. J., Verzicco, R. & Lohse, D.2014 Geostrophic convective turbulence: The effect of boundary layers. Preprint, arXiv:1409.6469.Google Scholar
Proudman, J. 1916 On the motion of solids in a liquid possessing vorticity. Proc. R. Soc. Lond. A 92, 408–424.Google Scholar
Rossby, H. T. 1969 A study of Bénard convection with and without rotation. J. Fluid Mech. 36, 309–335.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12 (7), 075022.Google Scholar
Shishkina, O. & Wagner, C. 2005 A fourth-order accurate finite volume scheme for numerical simulations of turbulent Rayleigh–Bénard convection in cylindrical containers. C. R. Méc. 333, 17–28.CrossRefGoogle Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.Google Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2010a Boundary layers in rotating weakly turbulent Rayleigh–Bénard convection. Phys. Fluids 22, 085103.Google Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2010b Optimal Prandtl number for heat transfer in rotating Rayleigh–Bénard convection. New J. Phys. 12 (7), 075005.CrossRefGoogle Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2012 Breakdown of the large-scale circulation in ${\it\Gamma}={\textstyle \frac{1}{2}}$ rotating Rayleigh–Bénard flow. Phys. Rev. E 86 (5), 056311.Google Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2013 Heat transport and flow structure in rotating Rayleigh–Bénard convection. Eur. J. Mech. (B/Fluids) 40, 41–49.CrossRefGoogle Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl and Rayleigh number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.Google Scholar
Stevens, R. J. A. M., Zhong, J.-Q., Clercx, H. J. H., Ahlers, G. & Lohse, D. 2009 Transitions between turbulent states in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 103, 024503.Google Scholar
Swarztrauber, P. N. & Sweet, R.1975 Efficient fortran subprograms for the solution of elliptic equations. Tech. Note IA-109. National Center for Atmospheric Research, Boulder, CO.Google Scholar
Taylor, G. I. 1921 Experiments with rotating fluids. Proc. R. Soc. Lond. 100, 114–121.Google Scholar
Weiss, S. & Ahlers, G. 2011a Heat transport by turbulent rotating Rayleigh–Bénard convection and its dependence on the aspect ratio. J. Fluid Mech. 684, 407–426.Google Scholar
Weiss, S. & Ahlers, G. 2011b The large-scale flow structure in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 461–492.Google Scholar
Weiss, S., Stevens, R. J. A. M., Zhong, J.-Q., Clercx, H. J. H., Lohse, D. & Ahlers, G. 2010 Finite-size effects lead to supercritical bifurcations in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 105, 224501.Google Scholar
Zhong, F., Ecke, R. & Steinberg, V. 1991 Asymmetric modes and the transition to vortex structures in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 67 (18), 2473–2476.Google Scholar
Zhong, J.-Q. & Ahlers, G. 2010 Heat transport and the large-scale circulation in rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 665, 300–333.Google Scholar
Zhong, J.-Q., Stevens, R. J. A. M., Clercx, H. J. H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102 (4), 044502.Google Scholar