Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-16T19:57:19.748Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal length elements of extended affine Weyl groups

Part of: Special aspects of infinite or finite groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  19 August 2014

Xuhua He  and
Sian Nie
Xuhua He
Affiliation:
Department of Mathematics, The Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong email maxhhe@ust.hk Current address: Department of Mathematics, University of Maryland, College Park, MD 20742, USA
Sian Nie
Affiliation:
Institute of Mathematics, Chinese Academy of Sciences, 100190 Beijing, China email niesian@amss.ac.cn Current address: Max Planck Institute for Mathematics, Vivatsgasse 753111 Bonn, Germany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

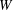Let $W$ be an extended affine Weyl group. We prove that the minimal length elements 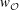$w_{{\mathcal{O}}}$ of any conjugacy class 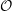${\mathcal{O}}$ of 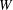$W$ satisfy some nice properties, generalizing results of Geck and Pfeiffer [On the irreducible characters of Hecke algebras, Adv. Math. 102 (1993), 79–94] on finite Weyl groups. We also study a special class of conjugacy classes, the straight conjugacy classes. These conjugacy classes are in a natural bijection with the Frobenius-twisted conjugacy classes of some 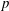$p$-adic group and satisfy additional interesting properties. Furthermore, we discuss some applications to the affine Hecke algebra 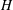$H$. We prove that 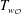$T_{w_{{\mathcal{O}}}}$, where 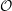${\mathcal{O}}$ ranges over all the conjugacy classes of 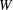$W$, forms a basis of the cocenter 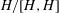$H/[H,H]$. We also introduce the class polynomials, which play a crucial role in the study of affine Deligne–Lusztig varieties He [Geometric and cohomological properties of affine Deligne–Lusztig varieties, Ann. of Math. (2) 179 (2014), 367–404].

Keywords

minimal length elementsaffine Weyl groupsaffine Hecke algebras

MSC classification

Primary: 20E45: Conjugacy classes 20F55: Reflection and Coxeter groups
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 11 , November 2014 , pp. 1903 - 1927
Copyright
© The Author(s) 2014 

References

Bonnafé, C. and Rouquier, R., Affineness of Deligne–Lusztig varieties for minimal length elements, J. Algebra 320 (2008), 1200–1206.CrossRefGoogle Scholar
Bourbaki, N., Lie groups and Lie algebras, Elements of Mathematics (Springer, Berlin, 2002), Chapters 4–6.Google Scholar
Digne, F. and Michel, J., Endomorphisms of Deligne–Lusztig varieties, Nagoya Math. J. 183 (2006), 35–103.CrossRefGoogle Scholar
Flicker, Y. Z., Bernstein’s isomorphism and good forms, in K-Theory and algebraic geometry: connections with quadratic forms and division algebras, Proceedings of Symposia in Pure Mathematics, vol. 58 (American Mathematical Society, Providence, RI, 1995), 171–196.Google Scholar
Geck, M., Kim, S. and Pfeiffer, G., Minimal length elements in twisted conjugacy classes of finite Coxeter groups, J. Algebra 229 (2000), 570–600.CrossRefGoogle Scholar
Geck, M. and Pfeiffer, G., On the irreducible characters of Hecke algebras, Adv. Math. 102 (1993), 79–94.CrossRefGoogle Scholar
Geck, M. and Pfeiffer, G., Characters of finite Coxeter groups and Iwahori–Hecke algebras, London Mathematical Society Monographs, New Series, vol. 21 (The Clarendon Press, Oxford University Press, New York, NY, 2000).Google Scholar
Geck, M. and Rouquier, R., Centers and simple modules for Iwahori–Hecke algebras, in Finite reductive groups, Luminy, 1994, Progress in Mathematics, vol. 141 (Birkhäuser, Boston, MA, 1997), 251–272.Google Scholar
Görtz, U., He, X. and Nie, S., $P$-alcoves and nonemptiness of affine Deligne–Lusztig varieties, Ann. Sci. Èc. Norm. Super. (4), to appear, math.AG/1211.3784.Google Scholar
He, X., Minimal length elements in some double cosets of Coxeter groups, Adv. Math. 215 (2007), 469–503.Google Scholar
He, X., Minimal length elements in conjugacy classes of extended affine Weyl group, Preprint (2010), math.RT/1004.4040. A shorter version for ${\tilde{A}}$ is available athttp://www.math.ust.hk/∼maxhhe/affA.pdf.Google Scholar
He, X., Geometric and cohomological properties of affine Deligne–Lusztig varieties, Ann. of Math. (2) 179 (2014), 367–404.CrossRefGoogle Scholar
He, X. and Lusztig, G., A generalization of Steinberg’s cross-section, J. Amer. Math. Soc. 25 (2012), 739–757.CrossRefGoogle Scholar
He, X. and Nie, S., Minimal length elements of finite Coxeter groups, Duke Math. J. 161 (2012), 2945–2967.Google Scholar
Iwahori, N. and Matsumoto, H., On some Bruhat decomposition and the structure of the Hecke rings of p-adic Chevalley groups, Publ. Math. Inst. Hautes Études Sci. 25 (1965), 5–48.Google Scholar
Kazhdan, D., Representations of groups over close local fields, J. Anal. Math. 47 (1986), 175–179.Google Scholar
Krammer, D., The conjugacy problem for Coxeter groups, Groups Geom. Dyn. 3 (2009), 71–171.CrossRefGoogle Scholar
Lusztig, G., Cells in affine Weyl groups, II, J. Algebra 109 (1987), 536–548.CrossRefGoogle Scholar
Lusztig, G., Cells in affine Weyl groups, III, J. Fac. Sci. Univ. Tokyo. 34 (1987), 223–243.Google Scholar
Lusztig, G., From conjugacy classes in the Weyl group to unipotent classes, Represent. Theory 15 (2011), 494–530.Google Scholar
Lusztig, G., On certain varieties attached to a Weyl group element, Bull. Inst. Math. Acad. Sin. (N.S.) 6 (2011), 377–414.Google Scholar
Orlik, S. and Rapoport, M., Deligne–Lusztig varieties and period domains over finite fields, J. Algebra 320 (2008), 1220–1234.CrossRefGoogle Scholar
Speyer, D. E., Powers of Coxeter elements in infinite groups are reduced, Proc. Amer. Math. Soc. 137 (2009), 1295–1302.Google Scholar
Springer, T. A., Regular elements of finite reflection groups, Invent. Math. 25 (1974), 159–198.Google Scholar