Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-20T02:43:57.728Z Has data issue: false hasContentIssue false
  • English
  • Français

On Grothendieck–Serre’s conjecture concerning principal $G$-bundles over reductive group schemes: I

Part of: Algebraic groups Linear algebraic groups and related topics

Published online by Cambridge University Press:  28 October 2014

I. Panin ,
A. Stavrova  and
N. Vavilov
I. Panin
Affiliation:
St. Petersburg Department of V. A. Steklov Institute of Mathematics of the Russian Academy of Sciences, 27 Fontanka, St. Petersburg, Russia Department of Mathematics and Mechanics of St. Petersburg State University, 28 Universitetsky pr., Peterhof, St. Petersburg, Russia email paniniv@gmail.com
A. Stavrova
Affiliation:
Department of Mathematics and Mechanics of St. Petersburg State University, 28 Universitetsky pr., Peterhof, St. Petersburg, Russia email anastasia.stavrova@gmail.com
N. Vavilov
Affiliation:
Department of Mathematics and Mechanics of St. Petersburg State University, 28 Universitetsky pr., Peterhof, St. Petersburg, Russia email nikolai-vavilov@yandex.ru
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

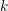Let $k$ be an infinite field. Let 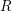$R$ be the semi-local ring of a finite family of closed points on a 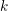$k$-smooth affine irreducible variety, let 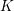$K$ be the fraction field of 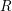$R$, and let 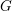$G$ be a reductive simple simply connected 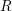$R$-group scheme isotropic over 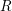$R$. Our Theorem 1.1 states that for any Noetherian 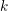$k$-algebra 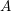$A$ the kernel of the map

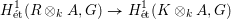$$\begin{eqnarray}H_{\acute{\text{e}}\text{t}}^{1}(R\otimes _{k}A,G)\rightarrow H_{\acute{\text{e}}\text{t}}^{1}(K\otimes _{k}A,G)\end{eqnarray}$$
induced by the inclusion of $R$ into 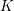$K$ is trivial. Theorem 1.2 for 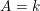$A=k$ and some other results of the present paper are used significantly in Fedorov and Panin [A proof of Grothendieck–Serre conjecture on principal bundles over a semilocal regular ring containing an infinite field, Preprint (2013), arXiv:1211.2678v2] to prove the Grothendieck–Serre’s conjecture for regular semi-local rings 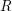$R$ containing an infinite field.

Keywords

reductive group schemesprincipal bundlesGrothendieck–Serre conjecture

MSC classification

Primary: 14L15: Group schemes 20G35: Linear algebraic groups over adèles and other rings and schemes 20G99: None of the above, but in this section 20G41: Exceptional groups
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 3 , March 2015 , pp. 535 - 567
Copyright
© The Author(s) 2014 

References

Artin, M., Comparaison avec la cohomologie classique: cas d’un préschéma lisse, in Théorie des topos et cohomologie étale des schémas (SGA 4), vol. 3, Exp. XI, Lecture Notes in Mathematics, vol. 305 (Springer, Berlin, 1973).Google Scholar
Bhatwadekar, S. M., Analitic isomorphismsms and category of finitely generated modules, Comm. Algebra 16 (1988), 1949–1958.Google Scholar
Borel, A. and Tits, J., Homomorphismes ‘abstraits’ de groupes algebriques simples, Ann. of Math. (2) 97 (1973), 499–571.Google Scholar
Chernousov, V., Variations on a theme of groups splitting by a quadratic extension and Grothendieck–Serre conjecture for group schemes F 4 with trivial g 3 invariant, Doc. Math. Extra volume (2010), 147–169.Google Scholar
Colliot-Thélène, J.-L. and Ojanguren, M., Espaces Principaux Homogènes Localement Triviaux, Publ. Math. Inst. Hautes Études Sci. 75 (1992), 97–122.Google Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., Principal homogeneous spaces under flasque tori: applications, J. Algebra 106 (1987), 148–205.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné): III. Étude cohomologique des faisceaux cohérents, Première partie, Publ. Math. Inst. Hautes Études Sci. 11 (1961), 5–167.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné): IV. Étude locale des schémas et des morphismes de schémas, Seconde partie, Publ. Math. Inst. Hautes Études Sci. 24 (1965), 5–231.Google Scholar
Eisenbud, D., Commutative algebra with a view toward algebraic geometry, Graduate Texts in Mathematics, vol. 150 (Springer, New York, 1995).Google Scholar
Fedorov, R. and Panin, I., A proof of Grothendieck–Serre conjecture on principal bundles over a semilocal regular ring containing an infinite field, Preprint (2013), arXiv:1211.2678v2.Google Scholar
Gille, P., Le probl‘eme de Kneser-Tits, Séminaire Bourbaki 983 (2007), 983-01–983-39.Google Scholar
Grothendieck, A., Torsion homologique et section rationnalles, in Anneaux de Chow et applications, Séminaire Chevalley, 2-e année (Secrétariat mathématique, Paris, 1958).Google Scholar
Grothendieck, A., Le groupe de Brauer II, in Dix exposés sur la cohomologique de schémas (North-Holland, Amsterdam, 1968).Google Scholar
Haboush, W. J., Reductive groups are geometrically reductive, Ann. of Math. (2) 102 (1975), 67–83.Google Scholar
Morel, F. and Voevodsky, V., A 1-homotopy theory of schemes, Publ. Math. Inst. Hautes Études Sci. 90 (1999), 45–143.Google Scholar
Moser, L.-F., Rational triviale Torseure und die Serre-Grothendiecksche Vermutung, Diplomarbeit, Mathematisches Institut der Ludwig-Maximilians Universitat Muenchen (2008), http://www.mathematik.uni-muenchen.de/∼lfmoser/da.pdf.Google Scholar
Mumford, D., Abelian varieties (Oxford University Press, Oxford, 1970).Google Scholar
Nagata, M., Invariants of a group in an affine ring, J. Math. Kyoto Univ. 3 (1964), 369–377.Google Scholar
Nisnevich, E. A., Affine homogeneous spaces and finite subgroups of arithmetic groups over function fields, Funct. Anal. Appl. 11 (1977), 64–66.Google Scholar
Nisnevich, Y., Rationally trivial principal homogeneous spaces and arithmetic of reductive group schemes over Dedekind rings, C. R. Acad. Sci. Paris Sér. I 299 (1984), 5–8.Google Scholar
Ojanguren, M. and Panin, I., A purity theorem for the Witt group, Ann. Sci. Éc. Norm. Supér. (4) 32 (1999), 71–86.Google Scholar
Ojanguren, M. and Panin, I., Rationally trivial hermitian spaces are locally trivial, Math. Z. 237 (2001), 181–198.Google Scholar
Ojanguren, M., Panin, I. and Zainoulline, K., On the norm principle for quadratic forms, J. Ramanujan Math. Soc. 19 (2004), 1–12.Google Scholar
Ojanguren, M. and Sridharan, R., Cancellation of Azumaya algebras, J. Algebra 18 (1971), 501–505.CrossRefGoogle Scholar
Panin, I., A purity theorem for linear algebraic groups, Preprint (2005),http://www.math.uiuc.edu/K-theory/0729.Google Scholar
Panin, I., On Grothendieck–Serre’s conjecture concerning principal $G$-bundles over reductive group schemes: II, Preprint (2013), arXiv:0905.1423v3.CrossRefGoogle Scholar
Panin, I. and Suslin, A., On a conjecture of Grothendieck concerning Azumaya algebras, St. Petersburg Math. J. 9 (1998), 851–858.Google Scholar
Panin, I., Petrov, V. and Stavrova, A., On Grothendieck–Serre’s for simple adjoint group schemes of types $E_{6}$and $E_{7}$, Preprint (2009), http://www.math.uiuc.edu/K-theory/.Google Scholar
Parimala, R., Indecomposable quadratic spaces over the affine plane, Adv. Math. 62 (1986), 1–6.Google Scholar
Petrov, V. and Stavrova, A., Grothendieck–Serre conjecture for groups of type $F_{4}$with trivial $f_{3}$invariant, Preprint (2009), http://www.mathematik.uni-bielefeld.de/LAG/man/374.html.Google Scholar
Popescu, D., General Néron desingularization and approximation, Nagoya Math. J. 104 (1986), 85–115.Google Scholar
Raghunathan, M. S., Principal bundles on affine space and bundles on the projective line, Math. Ann. 285 (1989), 309–332.Google Scholar
Raghunathan, M. S., Principal bundles admitting a rational section, Invent. Math. 116 (1994), 409–423.Google Scholar
Raghunathan, M. S., Erratum: principal bundles admitting a rational section, Invent. Math. 121 (1995), 223.Google Scholar
Raghunathan, M. S. and Ramanathan, A., Principal bundles on the affine line, Proc. Indian Acad. Sci. Math. Sci. 93 (1984), 137–145.Google Scholar
Serre, J.-P., Espaces fibrés algébriques, in Anneaux de Chow et applications, Séminaire Chevalley, 2-e année (Secrétariat mathématique, Paris, 1958).Google Scholar
Demazure, M. and Grothendieck, A., Schémas en groupes (SGA3), Lecture Notes in Mathematics, vol. 151–153 (Springer, Berlin, 1970).Google Scholar
Swan, R. G., Néron—Popescu desingularization, in Algebra and geometry, Taipei, 1995, Lectures in Algebra and Geometry, vol. 2 (International Press, Cambridge, MA, 1998), 135–192.Google Scholar
Tits, J., Algebraic and abstract simple groups, Ann. of Math. (2) 80 (1964), 313–329.Google Scholar
Voevodsky, V., Cohomological theory of presheaves with transfers, in Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies (Princeton University Press, Princeton, NJ, 2000).Google Scholar
Zainoulline, K. V., On Grothendieck’s conjecture on principal homogeneous spaces for some classical algebraic groups, St. Petersburg Math. J. 12 (2001), 117–143.Google Scholar