Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-25T02:04:57.563Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SOLUTIONS TO NONHOMOGENEOUS ALGEBRAIC DIFFERENTIAL EQUATIONS AND THEIR APPLICATION

Part of: Entire and meromorphic functions, and related topics Differential equations in the complex domain

Published online by Cambridge University Press:  24 September 2014

LIANG-WEN LIAO  and
ZHUAN YE
LIANG-WEN LIAO*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing, PR China email maliao@nju.edu.cn
ZHUAN YE
Affiliation:
Department of Mathematical Sciences, Northern Illinois University, DeKalb, IL 60115, USA email ye@math.niu.edu Department of Mathematics, Taiyuan University of Technology, Taiyuan, Shanxi, PR China
*
✉maliao@nju.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider solutions to the algebraic differential equation $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}f^nf'+Q_d(z,f)=u(z)e^{v(z)}$, where 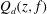$Q_d(z,f)$ is a differential polynomial in 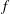$f$ of degree 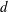$d$ with rational function coefficients, $u$ is a nonzero rational function and $v$ is a nonconstant polynomial. In this paper, we prove that if 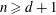$n\ge d+1$ and if it admits a meromorphic solution 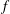$f$ with finitely many poles, then

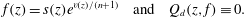$$\begin{equation*} f(z)=s(z)e^{v(z)/(n+1)} \quad \mbox {and}\quad Q_d(z,f)\equiv 0. \end{equation*}$$
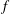With this in hand, we also prove that if $f$ is a transcendental entire function, then $f'p_k(f)+q_m(f)$ assumes every complex number $\alpha $, with one possible exception, infinitely many times, where 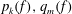$p_k(f), q_m(f)$ are polynomials in 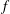$f$ with degrees 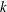$k$ and 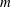$m$ with 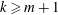$k\ge m+1$. This result generalizes a theorem originating from Hayman [‘Picard values of meromorphic functions and their derivatives’, Ann. of Math. (2)70(2) (1959), 9–42].

Keywords

nonlinear differential equationsentire solutionsmeromorphic solutionsNevanlinna theorynormal familyPicard values

MSC classification

Secondary: 34M05: Entire and meromorphic solutions 34M15: Algebraic aspects (differential-algebraic, hypertranscendence, group-theoretical) 30D35: Distribution of values, Nevanlinna theory
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 97 , Issue 3 , December 2014 , pp. 391 - 403
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Alotaibi, A. and Langley, J. K., ‘The separation of zeros of solutions of higher order linear differential equations with entire coefficients’, Results Math. 63(3–4) (2013), 1365–1373.Google Scholar
Chen, H., ‘Yosida functions and Picard values of integral functions and their derivatives’, Bull. Aust. Math. Soc. 54(3) (1996), 373–381.Google Scholar
Cherry, W. and Ye, Z., Nevanlinna’s Theory of Value Distribution, Springer Monographs in Mathematics (Springer, Berlin, 2001).Google Scholar
Chuaqui, M., Gröhn, J., Heittokangas, J. and Rättyä, J., ‘Zero separation results for solutions of second order linear differential equations’, Adv. Math. 245 (2013), 382–422.Google Scholar
Clunie, J., ‘On a result of Hayman’, J. Lond. Math. Soc. 42 (1967), 389–392.CrossRefGoogle Scholar
Gackstatter, F. and Laine, I., ‘Zur Theorie der gewöhnlichen Differentialgleichungen im Komplexen’, Ann. Polon. Math. 38(3) (1980), 259–287.Google Scholar
Hayman, W. K., ‘Picard values of meromorphic functions and their derivatives’, Ann. of Math. (2) 70(2) (1959), 9–42.Google Scholar
Hayman, W. K., Meromorphic Functions (Clarendon Press, Oxford, 1964).Google Scholar
He, Y. and Laine, I., ‘The Hayman–Miles theorem and the differential equation (y ′)n = R (z, y)’, Analysis 10(4) (1990), 387–396.Google Scholar
Heittokangas, J. and Rättyä, J., ‘Zero distribution of solutions of complex linear differential equations determines growth of coefficients’, Math. Nachr. 284(4) (2011), 412–420.Google Scholar
Laine, I., ‘Complex differential equations’, in: Handbook of Differential Equations: Ordinary Differential Equations, Vol. IV (Elsevier/North-Holland, Amsterdam, 2008), 269–363.Google Scholar
Li, P., ‘Entire solutions of certain type of differential equations II’, J. Math. Appl. 375 (2011), 310–319.Google Scholar
Liao, L. W., Yang, C. C. and Zhang, J. J., ‘On meromorphic solutions of certain type of nonlinear differential equations’, Ann. Acad. Sci. Fenn. Math. 38 (2013), 581–593.Google Scholar
Liao, L. W. and Ye, Z., ‘A class of second order differential equations’, Israel J. Math. 146 (2005), 281–301.CrossRefGoogle Scholar
Mues, E., ‘Zur Wertverteilung von Differentialpolynomen’, Arch. Math. (Basel) 32(1) (1979), 55–67.Google Scholar
Xu, Y., Wu, F. and Liao, L. W., ‘Picard values and normal families of meromorphic functions’, Proc. Roy. Soc. Edinburgh Sect. A 139(5) (2009), 1091–1099.Google Scholar
Yang, C. C. and Ye, Z., ‘Estimates of the proximate function of differential polynomials’, Proc. Japan Acad. Ser. A Math. Sci. 83(4) (2007), 50–55.Google Scholar
Yang, C. C. and Yi, H. X., Uniqueness Theory of Meromorphic Functions (Science Press and Kluwer Academic, Beijing, 2003).Google Scholar
Zalcman, L., ‘Normal families: new perspectives’, Bull. Amer. Math. Soc. 35 (1998), 215–230.Google Scholar
Zhang, Z. and Li, W., ‘The derivatives of polynomials of entire and meromorphic functions’, Chinese Ann. Math. Ser. A 15(2) (1994), 217–223 (in Chinese).Google Scholar
Zhang, J. and Liao, L., ‘Admissible meromorphic solutions of algebraic differential equations’, J. Math. Anal. Appl. 397(1) (2013), 225–232.Google Scholar