Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Piazza, Mario
and
Pulcini, Gabriele
2016.
Objectivity, Realism, and Proof.
Vol. 318,
Issue. ,
p.
245.
Kurahashi, Taishi
2016.
Henkin sentences and local reflection principles for Rosser provability.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 2,
p.
73.
PICOLLO, LAVINIA
2018.
REFERENCE IN ARITHMETIC.
The Review of Symbolic Logic,
Vol. 11,
Issue. 3,
p.
573.
Peregrin, Jaroslav
2018.
Truth, Existence and Explanation.
Vol. 334,
Issue. ,
p.
57.
Jerzak, Ethan
2019.
Non‐Classical Knowledge.
Philosophy and Phenomenological Research,
Vol. 98,
Issue. 1,
p.
190.
ROSSI, LORENZO
2019.
A UNIFIED THEORY OF TRUTH AND PARADOX.
The Review of Symbolic Logic,
Vol. 12,
Issue. 2,
p.
209.
Picollo, Lavinia
2020.
Alethic Reference.
Journal of Philosophical Logic,
Vol. 49,
Issue. 3,
p.
417.
DEAN, WALTER
2020.
INCOMPLETENESS VIA PARADOX AND COMPLETENESS.
The Review of Symbolic Logic,
Vol. 13,
Issue. 3,
p.
541.
Picollo, Lavinia
2020.
Reference and Truth.
Journal of Philosophical Logic,
Vol. 49,
Issue. 3,
p.
439.
CHENG, YONG
2021.
CURRENT RESEARCH ON GÖDEL’S INCOMPLETENESS THEOREMS.
The Bulletin of Symbolic Logic,
Vol. 27,
Issue. 2,
p.
113.
Rivas-Robledo, Pablo
2022.
HYPER-REF: A General Model of Reference for First-Order Logic and First-Order Arithmetic.
KRITERION – Journal of Philosophy,
Vol. 36,
Issue. 2,
p.
179.
Kennedy, Juliette
2022.
Gödel's Incompleteness Theorems.
KRIPKE, SAUL A.
2023.
GÖDEL’S THEOREM AND DIRECT SELF-REFERENCE.
The Review of Symbolic Logic,
Vol. 16,
Issue. 2,
p.
650.
GRABMAYR, BALTHASAR
and
VISSER, ALBERT
2023.
SELF-REFERENCE UPFRONT: A STUDY OF SELF-REFERENTIAL GÖDEL NUMBERINGS.
The Review of Symbolic Logic,
Vol. 16,
Issue. 2,
p.
385.
Grabmayr, Balthasar
2024.
A Step Towards Absolute Versions of Metamathematical Results.
Journal of Philosophical Logic,
Vol. 53,
Issue. 1,
p.
247.
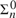 ${\rm{\Sigma }}_n^0$-truth or their own
${\rm{\Sigma }}_n^0$-truth or their own 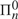 ${\rm{\Pi }}_n^0$-truth. Finally we offer an assessment of the results of both papers.
${\rm{\Pi }}_n^0$-truth. Finally we offer an assessment of the results of both papers.



