Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-07T17:06:01.025Z Has data issue: false hasContentIssue false
  • English
  • Français

On the rational K2 of a curve of GL2 type over a global field of positive characteristic

Published online by Cambridge University Press:  28 July 2014

Masataka Chida ,
Satoshi Kondo  and
Takuya Yamauchi
Masataka Chida
Affiliation:
Department of Mathematics, Kyoto University, Kitashirakawa Oiwake-cho, Sakyo-ku, Kyoto 606-8502, Japanchida@math.kyoto-u.ac.jp
Satoshi Kondo
Affiliation:
Kavli Institute for the Physics and Mathematics of the Universe, The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa, 277-8583, Japansatoshi.kondo@ipmu.jp
Takuya Yamauchi
Affiliation:
Department of mathematics, Faculty of Education, Kagoshima University, Korimoto 1-20-6 Kagoshima 890-0065, Japan Department of mathematics, University of Toronto, Toronto, Ontario M5S 2E4, Canadayamauchi@edu.kagoshima-u.ac.jp, tyama@math.toronto.edu
Get access

Abstract

If 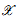is an integral model of a smooth curve X over a global field k, there is a localization sequence comparing the K-theory of 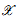and X. We show that K1 (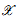) injects into K1(X) rationally, by showing that the previous boundary map in the localization sequence is rationally a surjection, for X of “GL2 type” and k of positive characteristic not 2. Examples are given to show that the relative G1 term can have large rank. Examples of such curves include non-isotrivial elliptic curves, Drinfeld modular curves, and the moduli of 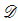-elliptic sheaves of rank 2.

Keywords

K-theoryfunction fieldsParshin conjecturePrimary 19F27Secondary 11G40
Type
Research Article
Information
Journal of K-Theory , Volume 14 , Issue 2 , October 2014 , pp. 313 - 342
Copyright
Copyright © ISOPP 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bloch, S. and Ogus, A., Gersten's conjecture and the homology of schemes (English), Ann. Sci. Éc. Norm. Supér. (4) 7 (1974), 181–201.CrossRefGoogle Scholar
2.Blum, A. and Stuhler, U., Drinfeld modules and elliptic sheaves (English), in Narasimhan, M. S. (ed.), Vector bundles on curves – new directions, Lectures given at the 3rd session of the Centro Internazionale Matematico Estivo (CIME) held in Cetraro (Cosenza), Italy, June 19-27, 1995. Berlin: Springer. Lecture Notes in Math. 1649, 110–188 (1997).Google Scholar
3.Bushnell, C. and Henniart, G., The local Langlands conjecture for GL(2), Grundlehren der Mathematischen Wissenschaften 335, Springer-Verlag, Berlin, New York, 2006.Google Scholar
4.Casselman, W., On some results of Atkin and Lehner, Math. Ann. 201 (1973), 301–31.CrossRefGoogle Scholar
5.Curtis, C. W. and Reiner, I., Representation theory of finite groups and associative algebras, Pure and Applied Mathematics XI, Interscience Publishers, a division of John Wiley & Sons, New York-London 1962 xiv+685 pp.Google Scholar
6.Deligne, P. and Husemöller, D., Survey of Drinfel'd modules, in Current trends in arith¬metical algebraic geometry, Proc. Summer Res. Conf., Arcata/Calif. 1985, Contemp. Math. 67 (1987), 25–91.Google Scholar
7.Deninger, C. and Murre, J., Motivic decomposition of abelian schemes and the Fourier transform (English), J. Reine Angew. Math. 422 (1991), 201–219.Google Scholar
8.Drinfel'd, V. G., Elliptic modules (English. Russian original), Math. USSR, Sb. 23 (1974), 561–592; translation from Mat. Sb., n. Ser. 94(136) (1974), 594-627.CrossRefGoogle Scholar
9.Drinfel'd, V. G., Langlands' conjecture for GL(2) over functional fields, Proceedings of the International Congress of Mathematics (Helsinki, 1978), Acad. Sci. Fennica, Helsinki, (1980), 565–574.Google Scholar
10.Geisser, T., Parshin's conjecture revisited (English), in Cortiñas, , Guillermo, (ed.) et al., K-theory and noncommutative geometry. Proceedings of the ICM 2006 satellite conference, Valladolid, Spain, August 31-September 6, 2006. Zürich: European Mathematical Society (EMS). EMS Series of Congress Reports, 413–425 (2008).Google Scholar
11.Gekeler, E.-U. and Reversat, M., Jacobians of Drinfeld modular curves, J. Reine Angew. Math. 476 (1996), 27–94.Google Scholar
12.Gillet, H., Riemann-Roch theorems for higher algebraic K-theory, Adv. Math. 40 (1981), 203–289.Google Scholar
13.Godement, R. and Jacquet, H., Zetafunctios of simple algebras, Lecture Notes on Math. 260, Springer-Verlag, Berlin and New York, (1972).Google Scholar
14.Grothendieck, A., Modèles de Néron et monodromie Groupes de monodromie en geometrie algebrique. I (French), Séminaire de Géométrie Algébrique du Bois-Marie 1967-1969 (SGA 7 I), Dirige par A. Grothendieck. Avec la collaboration de M. Raynaud et D. S. Rim. Lecture Notes in Math. 288. Springer-Verlag, Berlin-New York, 1972, pp. 313–523.Google Scholar
15.Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics 52. Springer-Verlag, New York-Heidelberg, 1977.Google Scholar
16.Hashimoto, K., On Brumer's family of RM-curves of genus two (English summary), Tohoku Math. J. (2) 52(4) (2000), 475–488.CrossRefGoogle Scholar
17.Jacquet, H., Generic representations, in Non-Commutative Harmonic Analysis, Lecture Notes in Math. 587, Springer-Verlag, Berlin and New York, 91–101, 1977.Google Scholar
18.Jacquet, H., Pricipal L-functions of the linear group, Automorphic forms, representations, and L-functios, part 2, Proc. Sympos. Pure Math. 33, Amer. Math. Soc., Providence, RI, 63–86, 1979.Google Scholar
19.Jacquet, H. and Langlands, R., Automorphic forms on GL(2), Lecture Notes in Math. 114, Springer-Verlag, Berlin and New York, 1970.Google Scholar
20.Jacquet, H. and Shalika, J.A., On Euler products and the classification of automorphic forms. II, Amer. J. Math. 103 (1981), 777–815.CrossRefGoogle Scholar
21.Jannsen, U., Mixed motives and algebraic K-theory, (Almost unchanged version of the author's habilitation at Univ. Regensburg 1988). (English), Lecture Notes in Math. 1400, Berlin etc.: Springer-Verlag. xi, 246 p.Google Scholar
22.Kondo, S. and Yasuda, S., On the second rational K-group of an elliptic curve over global fields of positive characteristic, Proc. London Math. Soc. (3) 102 (2011), 1053–1098.CrossRefGoogle Scholar
23.Kudla, S., The local Langlands correspondence: The non-archimedean case, in Motives, Proc. Symp. Pure Math. 55 (1994), 365–391.Google Scholar
24.Lafforgue, L., Chtoucas de Drinfeld et correspondance de Langlands, Invent. math. 147(1) (2002), 1–242.Google Scholar
25.Lang, S., Complex multiplication, Grundlehren der Mathematischen Wissenschaften 255, Springer-Verlag, New York, (1983).Google Scholar
26.Laumon, G., Rapoport, M. and Stuhler, U., -elliptic sheaves and the Langlands correspondence, Invent. Math. 113(2) (1993), 217–338.CrossRefGoogle Scholar
27.Liu, Q., Algebraic geometry and arithmetic curves, Oxford Graduate Texts in Mathematics 6, Oxford University Press, oxford, 2002. Translated from the French by Reinie Erné, Oxford Science Publications.Google Scholar
28.Liu, Q., Subgroups of semi-abelian varieties, available from http://www.math.u-bordeaux1.fr/~qliu/Notes/sub-abelian_varieties.pdfGoogle Scholar
29.Moret-Bailly, L., Pinceaux de variétés abéliennes, Astérisque 129 (1985).Google Scholar
30.Quillen, D., Higher algebraic K-theory. I (English), Ji, Lizhen (ed.) et al., Cohomology of groups and algebraic K-theory. Selected papers of the international summer school on cohomology of groups and algebraic K-theory, Hangzhou, China, July 1–3, 2007. Somerville, MA: International Press; Beijing: Higher Education Press. Advanced Lectures in Mathematics (ALM) 12, 413-478 (2010).Google Scholar
31.Ramakrishnan, D., Higher regulators on quaternionic Shimura curves and values of L-functions, Applications ofalgebraicK-theory to algebraic geometry and number theory, Part I, II (Boulder, Colo., 1983), 377–387, Contemp. Math. 55, Amer. Math. Soc., Providence, RI, (1986).Google Scholar
32.Rapoport, M. and Zink, T., Über die lokale Zetafunktion von Shimuravarietäten. Monodromiefiltration und verschwindende Zyklen in ungleicher Charakteristik., Invent. Math. 68(1) (1982), 21–101.CrossRefGoogle Scholar
33.Ribet, K., Abelian varieties over ℚ and modular forms, Modular curves and abelian varieties, 241–261, Progr. Math. 224 (2004), Birkhauser, Basel.Google Scholar
34.Rubin, K., Euler systems, Ann. of Math. Studies 147 (2000).Google Scholar
35.Shimura, G., Introduction to the arithmetic theory of automorphic functions, Publications of the Mathematical Society of Japan 11. Iwanami Shoten, Publishers, Tokyo; Princeton University Press, Princeton, N.J., 1971. xiv+267 pp.Google Scholar
36.Serre, J.P., Galois cohomology, Transl. from the French by Patrick Ion. 2nd printing. (English), Springer Monographs in Mathematics. Berlin: Springer. x, 210 p. (2002).Google Scholar
37.Scholl, A. J., Classical motives, Jannsen, Uwe (ed.) et al., Motives. Proceedings of the summer research conference on motives, held at the University of Washington, Seattle, WA, USA, July 20-August 2, 1991. Providence, RI: American Mathematical Society. Proc. Symp. Pure Math. 55(1) (1994), 163–187.Google Scholar
38.Soulé, C., Groupes de Chow et K-thorie de variétés sur un corps fini (French), Math. Ann. 268 (1984), 317–345.Google Scholar
39.Tamagawa, A., The Eisenstein quotient ofthe Jacobian variety ofa Drin'feld modular curve (English), Publ. Res. Inst. Math. Sci. 31(2) (1995), 203–246.Google Scholar
40.Tate, J., Endomorphisms of abelian varieties over finite fields, Invent. Math. 2 (1966), 134–144.CrossRefGoogle Scholar
41.Tate, J., Number theoretic background, Automorphic forms, representations and L - functions (Oregon State Univ., Corvallis, Ore., 1977), Proc. Symp. Pure Math. 33 Part 2, Amer. Math. Soc., Providence, R.I., 3–26 (1979).Google Scholar
42.Taylor, R., Galois representations, Annales de la Faculte des Sciences de Toulouse 13 (2004), 73–119.Google Scholar
43.Zarhin, Ju. G., Endomorphisms of Abelian varieties over fields of finite characteristic (Russian), Izv. Akad. Nauk SSSR Ser. Mat. 39(2) (1975), 272–277.Google Scholar