Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-16T18:20:22.000Z Has data issue: false hasContentIssue false
  • English
  • Français

Matrix factorizations via Koszul duality

Part of: Homological methods Local theory Homological algebra

Published online by Cambridge University Press:  17 July 2014

Junwu Tu
Junwu Tu*
Affiliation:
Mathematics Department, University of Oregon, Eugene, OR 97403, USA email junwut@uoregon.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we prove a version of curved Koszul duality for 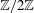$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{Z}/2\mathbb{Z}$-graded curved coalgebras and their cobar differential graded algebras. A curved version of the homological perturbation lemma is also obtained as a useful technical tool for studying curved (co)algebras and precomplexes. The results of Koszul duality can be applied to study the category of matrix factorizations 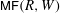$\mathsf{MF}(R,W)$. We show how Dyckerhoff’s generating results fit into the framework of curved Koszul duality theory. This enables us to clarify the relationship between the Borel–Moore Hochschild homology of curved (co)algebras and the ordinary Hochschild homology of the category 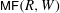$\mathsf{MF}(R,W)$. Similar results are also obtained in the orbifold case and in the graded case.

Keywords

Koszul dualitymatrix factorizationsHochschild homology

MSC classification

Secondary: 18G35: Chain complexes 14B05: Singularities 16E40: (Co)homology of rings and algebras (e.g. Hochschild, cyclic, dihedral, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 9 , September 2014 , pp. 1549 - 1578
Copyright
© The Author 2014 

References

Ballard, M., Favero, D. and Katzarkov, L., Orlov spectra: bounds and gaps, Invent. Math. 189 (2012), 359–430.Google Scholar
Bondal, A. and Van den Bergh, M., Generators and representability of functors in commutative and noncommutative geometry, Mosc. Math. J. 3 (2003), 1–36; 258.Google Scholar
Crainic, M., On the homological perturbation lemma, and deformations. Preprint (2004),arXiv:math/0403266.Google Scholar
Căldăraru, A. and Tu, J., Curved A-infinity algebras and Landau–Ginzburg models, New York J. Math. 19 (2013), 305–342.Google Scholar
Dyckerhoff, T., Compact generators in the categories of matrix factorizations, Duke Math. J. 159 (2011), 223–274.Google Scholar
Eisenbud, D., Homological algebra on a complete intersection, with an application to group representations, Trans. Amer. Math. Soc. 260 (1980), 35–64.Google Scholar
Keller, B., On the cyclic homology of exact categories, J. Pure Appl. Algebra. 136 (1999), 1–56.Google Scholar
Keller, B., Murfet, D. and Van den Bergh, M., On two examples by Iyama and Yoshino, Compositio Math. 147 (2011), 591–612.Google Scholar
Loday, J.-L. and Vallette, B., Algebraic Operads, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 346 (Springer, Heidelberg, 2012).Google Scholar
Neeman, A., The connection between the K-theory localisation theorem of Thomason, Trobaugh and Yao, and the smashing subcategories of Bousfield and Ravenel, Ann. Sci. Éc. Norm. Supér (4) 25 (1992), 547–566.Google Scholar
Orlov, D., Derived categories of coherent sheaves and triangulated categories of singularities, in Algebra, arithmetic, and geometry: in honor of Yu. I. Manin, Vol. II, Progress in Mathematics, vol. 270 (Birkhäuser, Boston, MA, 2009), 503–531.CrossRefGoogle Scholar
Polishchuk, A., A-infinity algebra of an elliptic curve and Eisenstein series, Comm. Math. Phys. 301 (2011), 709–722.Google Scholar
Positselski, L., Two kinds of derived categories, Koszul duality, and comodule–contramodule correspondence, Memoirs of the American Mathematical Society, vol. 212, no. 996 (American Mathematical Society, Providence, RI, 2011).Google Scholar
Segal, E., The closed state space of affine Landau–Ginzburg B-models, J. Noncommut. Geom. 7 (2013), 857–883.Google Scholar
Seidel, P., The derived category of the Fermat quintic threefold (after Kontsevich, Douglas, et al.), unpublished notes.Google Scholar