Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-23T19:02:26.388Z Has data issue: false hasContentIssue false
  • English
  • Français

On the emergence of non-classical decay regimes in multiscale/fractal generated isotropic turbulence

Published online by Cambridge University Press:  05 September 2014

Marcello Meldi ,
Hugo Lejemble  and
Pierre Sagaut
Marcello Meldi*
Affiliation:
Institut PPRIME, Department of Fluid Flow, Heat Transfer and Combustion, CNRS – Université de Poitiers – ENSMA, UPR 3346, SP2MI – Téléport, 211 Bd. Marie et Pierre Curie, B.P. 30179, F-86962 Futuroscope Chasseneuil CEDEX, France
Hugo Lejemble
Affiliation:
Institut Jean Le Rond d’Alembert, UMR 7190, 4 Place Jussieu, Case 162, Université Pierre et Marie Curie, Paris 6, F-75252 Paris CEDEX 5, France
Pierre Sagaut
Affiliation:
Laboratoire de Mécanique, Modélisation & Procédés Propres (M2P2), UMR CNRS 6181, Aix-Marseille Université, Technopôle de Château-Gombert, 38 Rue Frédéric Joliot-Curie, 13451 Marseille CEDEX, France
*
†Email address for correspondence: marcellomeldi@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The present paper addresses the issue of finding key parameters that may lead to the occurrence of non-classical decay regimes for fractal/multiscale generated grid turbulence. To this aim, a database of numerical simulations has been generated by the use of the eddy-damped quasi-normal Markovian (EDQNM) model. The turbulence production in the wake of the fractal/multiscale grid is modelled via a turbulence production term based on the forcing term developed for direct numerical simulations (DNS) purposes and the dynamics of self-similar wakes. The sensitivity of the numerical results to the simulation parameters has been investigated successively. The analysis is based on the observation of both the time evolution of the turbulent energy spectrum $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}E(k,t)$ and the decay of the flow statistical quantities, such as the turbulent kinetic energy 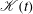$\mathcal{K}(t)$ and the energy dissipation rate $\varepsilon (t)$. A satisfactory agreement with existing experimental data published by different research teams is observed. In particular, it is observed that the key parameter that governs the nature of turbulence decay is 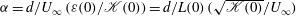$\alpha ={d/U_{\infty }}\, {(\varepsilon (0)/\mathcal{K}(0))}={d/L(0)} \, {(\sqrt{\mathcal{K}(0)}/U_{\infty })}$ (with $d$ the bar diameter and 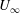$U_{\infty }$ the upstream uniform velocity), which measures the ratio of the time scale largest grid bar 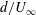$d/U_{\infty }$ to the turbulent time scale 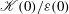$\mathcal{K}(0)/\varepsilon (0)$. Two asymptotic behaviours for 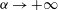$\alpha \rightarrow + \infty $ and $\alpha \rightarrow 0$ are identified: (i) a fast algebraic decay law regime for rapidly decaying production terms, due to strongly modified initial kinetic energy spectrum and (ii) a real exponential decay regime associated with strong, very slowly decaying production terms. The present observations are in full agreement with conclusions drawn from recent fractal grid experiments, and it provides a physical scenario for occurrence of anomalous decay regime which encompasses previous hypotheses.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence modelling
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 816 - 843
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Cambon, C., Mansour, N. N. & Godeferd, F. S. 1997 Energy transfer in rotating turbulence. J. Fluid Mech. 337, 303–332.Google Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25, 657–682.Google Scholar
Davidson, P. A. 2011 The minimum energy decay rate in quasi-isotropic grid turbulence. Phys. Fluids 23 (8), 085108.Google Scholar
Discetti, S., Natale, A. & Astarita, T. 2013 Spatial filtering improved tomographic PIV. Exp. Fluids 54, 1505–1517.CrossRefGoogle Scholar
Djenidi, L. & Tardu, S. F. 2012 On the anisotropy of a low-Reynolds-number grid turbulence. J. Fluid Mech. 702, 332–353.CrossRefGoogle Scholar
Ertunc, O., Ozyilmaz, N., Lienhart, H., Durst, F. & Beronov, K. 2010 Homogeneity of turbulence generated by static-grid structures. J. Fluid Mech. 654, 473–500.Google Scholar
Eyink, G. L. & Thomson, D. J. 2000 Free decay of turbulence and breakdown of self-similarity. Phys. Fluids 12, 477–479.Google Scholar
George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids A 4 (7), 1492–1509.Google Scholar
George, W. K. & Wang, H. 2009 The exponential decay of homogeneous turbulence. Phys. Fluids 21 (2), 025108.Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2012 Particle image velocimetry study of fractal-generated turbulence. J. Fluid Mech. 711, 306–336.Google Scholar
Hearst, R. J. & Lavoie, P. 2014 Decay of turbulence generated by a square-fractal-element grid. J. Fluid Mech. 741, 567–584.Google Scholar
Hurst, D. & Vassilicos, J. C. 2007 Scalings and decay of fractal-generated turbulence. Phys. Fluids 19, 035103.Google Scholar
Ishida, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.Google Scholar
Kang, H. S., Chester, S. & Meneveau, C. 2003 Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. J. Fluid Mech. 480, 129–160.Google Scholar
Krogstad, P. Å. & Davidson, P. A. 2011 Freely-decaying, homogeneous turbulence generated by multi-scale grids. J. Fluid Mech. 680, 417–434.Google Scholar
Krogstad, P. Å. & Davidson, P. A. 2012 Near-field investigation of turbulence produced by multi-scale grids. Phys. Fluids 24 (3), 035103.Google Scholar
Laizet, S. & Vassilicos, J. C. 2011 DNS of fractal-generated turbulence. Flow Turbul. Combust. 87, 673–705.Google Scholar
Lesieur, M. 2008 Turbulence in Fluids, 4th edn. Springer.Google Scholar
Lesieur, M., Montmory, C. & Chollet, J. P. 1987 The decay of kinetic energy and temperature variance in three-dimensional isotropic turbulence. Phys. Fluids 30, 1278–1286.Google Scholar
Lesieur, M. & Schertzer, D. 1978 Self-similar decay of high Reynolds-number turbulence. J. Méc. 17 (4), 609–646.Google Scholar
Makita, H. 1991 Realization of a large-scale turbulence field in a small wind tunnel. Fluid Dyn. Res. 8, 53–64.Google Scholar
Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson–Kolmogorov cascade. Phys. Fluids 22 (7), 075101.CrossRefGoogle Scholar
Mazzi, B. & Vassilicos, J. C. 2004 Fractal-generated turbulence. J. Fluid Mech. 502, 65–87.Google Scholar
Meldi, M. & Sagaut, P. 2012 On non-self-similar regimes in homogeneous isotropic turbulence decay. J. Fluid Mech. 711, 364–393.CrossRefGoogle Scholar
Meldi, M. & Sagaut, P. 2013a Further insights into self-similarity and self-preservation in freely decaying isotropic turbulence. J. Turbul. 14, 24–53.Google Scholar
Meldi, M. & Sagaut, P. 2013b Pressure statistics in self-similar freely decaying isotropic turbulence. J. Fluid Mech. 717, R2.Google Scholar
Meldi, M., Sagaut, P. & Lucor, D. 2011 A stochastic view of isotropic turbulence decay. J. Fluid Mech. 668, 351–362.Google Scholar
Meyers, J. & Meneveau, C. 2008 A functional form for the energy spectrum parametrizing Bottleneck and intermittency effects. Phys. Fluids 20 (6), 065109.Google Scholar
Mohamed, M. S. & LaRue, J. C. 1990 The decay power law in grid-generated turbulence. J. Fluid Mech. 219, 195–214.Google Scholar
Moser, M. D., Rogers, M. M. & Ewing, D. W. 1998 Self-similarity of time-evolving plane wakes. J. Fluid Mech. 367, 255–289.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Nagata, K., Sakai, Y., Inaba, T., Suzuki, H., Terashima, O. & Suzuki, H. 2013 Turbulence structure and turbulence kinetic energy transport in multiscale/fractal-generated turbulence. Phys. Fluids 25, 065102.Google Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Saffman, P. J. 1967 The large-scale structure of homogeneous turbulence. J. Fluid Mech. 27, 581–593.CrossRefGoogle Scholar
Sagaut, P. & Cambon, C. 2008 Homogenous Turbulence Dynamics. Cambridge University Press.Google Scholar
Seoud, R. E. & Vassilicos, J. C. 2007 Dissipation and decay of fractal-generated turbulence. Phys. Fluids 19, 105108.Google Scholar
Skrbek, L. & Stalp, S. R. 2000 On the decay of homogeneous isotropic turbulence. Phys. Fluids 12, 1997–2019.CrossRefGoogle Scholar
Speziale, C. G. & Bernard, P. S. 1992 The energy decay in self-preserving isotropic turbulence revisited. J. Fluid Mech. 241, 645–667.Google Scholar
Staicu, A., Mazzi, B., Vassilicos, J. C. & Van De Water, W. 2003 Turbulent wakes of fractal objects. Phys. Rev. E 67, 066306.Google Scholar
Taylor, G. I. 1935 Statistical Theory of Turbulence. Proc. R. Soc. Lond. A 151, 421–444.Google Scholar
Tchoufag, J., Sagaut, P. & Cambon, C. 2012 Spectral approach to finite Reynolds number effects on Kolmogorov’s 4/5 law in isotropic turbulence. Phys. Fluids 24 (1), 015107.Google Scholar
Thormann, A. & Meneveau, C. 2014 Decay of homogeneous, nearly isotropic turbulence behind active fractal grids. Phys. Fluids 26, 025112.CrossRefGoogle Scholar
Valente, P. C. & Vassilicos, J. C. 2011 The decay of turbulence generated by a class of multiscale grids. J. Fluid Mech. 687, 300–340.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2012 Universal dissipation scaling for non-equilibrium turbulence. Phys. Rev. Lett. 108, 214503.Google Scholar
Vassilicos, J. C. 2011 An infinity of possible invariants for decaying homogeneous turbulence. Phys. Lett. A 375, 1010–1013.Google Scholar
Von Karman, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. A 164, 192–215.Google Scholar
Von Karman, T. & Lin, C. C. 1949 On the concept of similarity in the theory of isotropic turbulence. Rev. Mod. Phys. 21 (3), 516–519.Google Scholar
Yeung, P. K., Donzis, D. & Sreenivasan, K. R. 2012 Dissipation, enstrophy and pressure statistics in turbulence simulations at high Reynolds numbers. J. Fluid Mech. 700, 5–15.Google Scholar