Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T10:42:05.745Z Has data issue: false hasContentIssue false
  • English
  • Français

A FURTHER PROPERTY OF SPHERICAL ISOMETRIES

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  15 May 2014

RYOTARO TANAKA
RYOTARO TANAKA*
Affiliation:
Department of Mathematical Science, Graduate School of Science and Technology, Niigata University, Niigata 950-2181, Japan email ryotarotanaka@m.sc.niigata-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

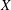In this paper, it is proved that every isometry between the unit spheres of two real Banach spaces preserves the frames of the unit balls. As a consequence, if $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}X$ and 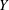$Y$ are $n$-dimensional Banach spaces and 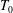$T_0$ is an isometry from the unit sphere of 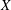$X$ onto that of $Y$ then it maps the set of all 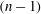$(n-1)$-extreme points of the unit ball of 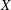$X$ onto that of 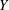$Y$.

Keywords

Tingley’s problemisometric extension problemframek-extreme point

MSC classification

Secondary: 46B04: Isometric theory of Banach spaces 46B20: Geometry and structure of normed linear spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 2 , October 2014 , pp. 304 - 310
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

An, G., ‘Isometries on unit sphere of (l β n)’, J. Math. Anal. Appl. 301 (2005), 249–254.CrossRefGoogle Scholar
Birkhoff, G., ‘Orthogonality in linear metric spaces’, Duke Math. J. 1(2) (1935), 169–172.CrossRefGoogle Scholar
Cheng, L. and Dong, Y., ‘On a generalized Mazur–Ulam question: Extension of isometries between unit spheres of Banach spaces’, J. Math. Anal. Appl. 377 (2011), 464–470.CrossRefGoogle Scholar
Day, M. M., ‘Polygons circumscribed about closed convex curves’, Trans. Amer. Math. Soc. 62 (1947), 315–319.CrossRefGoogle Scholar
Day, M. M., ‘Some characterizations of inner-product spaces’, Trans. Amer. Math. Soc. 62 (1947), 320–337.Google Scholar
Ding, G. G., ‘The isometric extension problem in the unit spheres of l p(Γ) (p > 1) type spaces’, Sci. China Ser. A. 46 (2003), 333–338.CrossRefGoogle Scholar
Ding, G. G., ‘On isometric extension problem between two unit spheres’, Sci. China Ser. A. 52 (2009), 2069–2083.CrossRefGoogle Scholar
Ding, G. G. and Li, J. Z., ‘Sharp corner points and isometric extension problem in Banach spaces’, J. Math. Anal. Appl. 405 (2013), 297–309.CrossRefGoogle Scholar
Holmes, R. B., Geometric Functional Analysis and its Applications, Graduate Texts in Mathematics, 24 (Springer, New York, 1975).Google Scholar
Hou, Z. B. and Zhang, L. J., ‘Isometric extension of a nonsurjective isometric mapping between the unit spheres of A L p-spaces (1 < p < ∞)’, Acta Math. Sinica (Chin. Ser.) 50 (2007), 1435–1440.Google Scholar
James, R. C., ‘Orthogonality in normed linear spaces’, Duke Math. J. 12 (1945), 291–302.CrossRefGoogle Scholar
James, R. C., ‘Inner products in normed linear spaces’, Bull. Amer. Math. Soc. 53 (1947), 559–566.Google Scholar
James, R. C., ‘Orthogonality and linear functionals in normed linear spaces’, Trans. Amer. Math. Soc. 61 (1947), 265–292.Google Scholar
Jiménez-Melado, A., Llorens-Fuster, E. and Mazcuñán-Navarro, E. M., ‘The Dunkl–Williams constant, convexity, smoothness and normal structure’, J. Math. Anal. Appl. 342 (2008), 298–310.CrossRefGoogle Scholar
Kadets, V. and Martín, M., ‘Extension of isometries between unit spheres of finite-dimensional polyhedral Banach spaces’, J. Math. Anal. Appl. 396 (2012), 441–447.CrossRefGoogle Scholar
Liu, R., ‘Isometries between the unit spheres of l β-sum of strictly convex normed spaces’, Acta Math. Sinica (Chan. Ser.) 50 (2007), 227–232.Google Scholar
Mankiewicz, P., ‘On extension of isometries in normed linear spaces’, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 20 (1972), 367–371.Google Scholar
Mizuguchi, H., Saito, K.-S. and Tanaka, R., ‘On the calculation of the Dunkl-Williams constant of normed linear spaces’, Cent. Eur. J. Math. 11(7) (2013), 1212–1227.Google Scholar
Tan, D. N. and Liu, R., ‘A note on the Mazur–Ulam property of almost-CL-spaces’, J. Math. Anal. Appl. 405 (2013), 336–341.Google Scholar
Tanaka, R., ‘Tingley’s problem on symmetric absolute normalized norms on $\mathbb{R}^2$’, Acta Math. Sin. (Engl. Ser.), to appear.Google Scholar
Tanaka, R., ‘On the frame of the unit ball of Banach spaces’, Cent. Eur. J. Math., to appear.Google Scholar
Tingley, D., ‘Isometries of the unit sphere’, Geom. Dedicata 22 (1987), 371–378.CrossRefGoogle Scholar
Wang, J., ‘On extension of isometries between unit spheres of A L p-spaces (0 < p < ∞)’, Proc. Amer. Math. Soc. 132 (2004), 2899–2909.Google Scholar
Yang, X., ‘On extension of isometries between unit spheres of L p(μ) and L p(ν, H) (1 < p≠2, H is a Hilbert space)’, J. Math. Anal. Appl. 323 (2006), 985–992.CrossRefGoogle Scholar