Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-26T08:25:50.935Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Importance Sampling of Self-Avoiding Walks

Published online by Cambridge University Press:  20 January 2014

MIREILLE BOUSQUET-MÉLOU
MIREILLE BOUSQUET-MÉLOU*
Affiliation:
MBM: CNRS, LaBRI, Université Bordeaux 1, 351 Cours de la Libération, 33405 Talence, France (e-mail: mireille.bousquet@labri.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

In a 1976 paper published in Science, Knuth presented an algorithm to sample (non-uniform) self-avoiding walks crossing a square of side k. From this sample, he constructed an estimator for the number of such walks. The quality of this estimator is directly related to the (relative) variance of a certain random variable Xk. From his experiments, Knuth suspected that this variance was extremely large (so that the estimator would not be very efficient). But how large? For the analogous Rosenbluth algorithm, which samples unconfined self-avoiding walks of length n, the variance of the corresponding estimator is believed to be exponential in n.

A few years ago, Bassetti and Diaconis showed that, for a sampler à la Knuth that generates walks crossing a k × k square and consisting of North and East steps, the relative variance is only 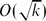$O(\sqrt k)$. In this note we take one step further and show that, for walks consisting of North, South and East steps, the relative variance jumps to 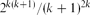$2^{k(k+1)}/(k+1)^{2k}$. This is exponential in the average length of the walks, which is of order k2. We also obtain partial results for general self-avoiding walks crossing a square, suggesting that the relative variance could be exponential in k2 (which is again the average length of these walks).

Knuth's algorithm is a basic example of a widely used technique called sequential importance sampling. The present paper, following the paper by Bassetti and Diaconis, is one of very few examples where the variance of the estimator can be found.

Keywords

Primary 05A15Secondary 60C05
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 5: Honouring the Memory of Philippe Flajolet - Part 1 , September 2014 , pp. 725 - 748
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Abbott, H. L. and Hanson, D. (1978) A lattice path problem. Ars Combin. 6 163–178.Google Scholar
[2]Bacher, A. Generalized Dyck paths of bounded height. arXiv:1303.2724.Google Scholar
[3]Bacher, A. and Bousquet-Mélou, M. (2011) Weakly directed self-avoiding walks. J. Combin. Theory Ser. A 118 2365–2391.Google Scholar
[4]Banderier, C., Bousquet-Mélou, M., Denise, A., Flajolet, P., Gardy, D. and Gouyou-Beauchamps, D. (2002) Generating functions for generating trees. Discrete Math. 246 29–55.Google Scholar
[5]Bassetti, F. and Diaconis, P. (2006) Examples comparing importance sampling and the Metropolis algorithm. Illinois J. Math. 50 67–91.CrossRefGoogle Scholar
[6]Batoulis, J. and Kremer, K. (1988) Statistical properties of biased sampling methods for long polymer chains. J. Phys. A 21 127–146.Google Scholar
[7]Bousquet-Mélou, M., Guttmann, A. J. and Jensen, I. (2005) Self-avoiding walks crossing a square. J. Phys. A 38 9159–9181.CrossRefGoogle Scholar
[8]Bousquet-Mélou, M. and Petkovšek, M. (2000) Linear recurrences with constant coefficients: the multivariate case. Discrete Math. 225 51–75.Google Scholar
[9]Chan, Y.-B. and Rechnitzer, A. (2012) A Monte Carlo study of non-trapped self-avoiding walks. J. Phys. A 45 405004.Google Scholar
[10]Chen, Y., Diaconis, P., Holmes, S. P. and Liu, J. S. (2005) Sequential Monte Carlo methods for statistical analysis of tables. J. Amer. Statist. Assoc. 100 109–120.Google Scholar
[11]Blitzstein, J. and Diaconis, P. (2010) A sequential importance sampling algorithm for generating random graphs with prescribed degrees. Internet Math. 6 (4)489–522.CrossRefGoogle Scholar
[12]Flajolet, P. and Sedgewick, R. (2009) Analytic Combinatorics, Cambridge University Press.Google Scholar
[13]Kennedy, T. (2002) A faster implementation of the pivot algorithm for self-avoiding walks. J. Statist. Phys. 106 407–429.Google Scholar
[14]Knuth, D. E. (1976) Mathematics and computer science: coping with finiteness. Science 194 1235–1242.Google Scholar
[15]Knuth, D. E. (1996) Selected papers on computer science, Vol. 59 of CSLI Lecture Notes, CSLI Publications.Google Scholar
[16]Madras, N. (1995) Critical behaviour of self-avoiding walks that cross a square. J. Phys. A 28 1535–1547.CrossRefGoogle Scholar
[17]Madras, N. and Slade, G. (1993) The Self-Avoiding Walk, Probability and its Applications, Birkhäuser.Google Scholar
[18]Majid, I., Jan, N., Coniglio, A. and Stanley, H. E. (1984) Kinetic growth walk: A new model for linear polymers. Phys. Rev. Lett. 52 1257–1260.Google Scholar
[19]Owczarek, A. L. and Prellberg, T. (2008) Scaling of the atmosphere of self-avoiding walks. J. Phys. A 41 375004.Google Scholar
[20]Prodinger, H. (2003/04) The kernel method: A collection of examples. Sém. Lothar. Combin. 50 B50f.Google Scholar
[21]Rosenbluth, M. N. and Rosenbluth, A. W. (1955) Monte Carlo calculation of the average extension of molecular chains. J. Chem. Phys. 23 356–359.Google Scholar
[22]Stanley, R. P. (1997) Enumerative Combinatorics I, Vol. 49 of Cambridge Studies in Advanced Mathematics. Cambridge University Press.Google Scholar