Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-16T10:17:42.163Z Has data issue: false hasContentIssue false
  • English
  • Français

INVERSE BERNSTEIN INEQUALITIES AND MIN–MAX–MIN PROBLEMS ON THE UNIT CIRCLE

Part of: Geometric function theory Approximations and expansions Polynomials and matrices General convexity

Published online by Cambridge University Press:  13 August 2014

Tamás Erdélyi ,
Douglas P. Hardin  and
Edward B. Saff
Tamás Erdélyi
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX 77843, U.S.A. email terdelyi@math.tamu.edu
Douglas P. Hardin
Affiliation:
Center for Constructive Approximation, Department of Mathematics, Vanderbilt University, Nashville, TN 37240, U.S.A. email doug.hardin@vanderbilt.edu
Edward B. Saff
Affiliation:
Center for Constructive Approximation, Department of Mathematics, Vanderbilt University, Nashville, TN 37240, U.S.A. email edward.b.saff@vanderbilt.edu
Get access

Abstract

We give a short and elementary proof of an inverse Bernstein-type inequality found by S. Khrushchev for the derivative of a polynomial having all its zeros on the unit circle. The inequality is used to show that equally-spaced points solve a min–max–min problem for the logarithmic potential of such polynomials. Using techniques recently developed for polarization (Chebyshev-type) problems, we show that this optimality also holds for a large class of potentials, including the Riesz potentials 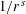$1/r^{s}$ with 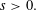$s>0.$

MSC classification

Primary: 11C08: Polynomials 30C15: Zeros of polynomials, rational functions, and other analytic functions (e.g. zeros of functions with bounded Dirichlet integral) 41A17: Inequalities in approximation (Bernstein, Jackson, Nikol'skiĭ-type inequalities) 52A40: Inequalities and extremum problems
Type
Research Article
Information
Mathematika , Volume 61 , Issue 3 , September 2015 , pp. 581 - 590
Copyright
Copyright © University College London 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrus, G., Analytic and Probabilistic Problems in Discrete Geometry. PhD Thesis, University College London, 2009.Google Scholar
Ambrus, G., Ball, K. and Erdélyi, T., Chebyshev constants for the unit circle. Bull. Lond. Math. Soc. 45(2) 2013, 236–248.CrossRefGoogle Scholar
Bernstein, S. N., Leçons sur les Propriétés Extrémales et la Meilleure Approximation des Fonctions Analytiques d’une Variable Réelle. Gauthier-Villars (Paris, 1926).Google Scholar
Borwein, P. and Erdélyi, T., Polynomials and Polynomial Inequalities. Springer (New York, NY, 1995).CrossRefGoogle Scholar
Brauchart, J. S., Hardin, D. P. and Saff, E. B., The Riesz energy of the Nth roots of unity: an asymptotic expansion for large N. Bull. Lond. Math. Soc. 41(4) 2009, 621–633.CrossRefGoogle Scholar
DeVore, R. A. and Lorentz, G. G., Constructive Approximation. Springer (Berlin, Heidelberg, 1993).CrossRefGoogle Scholar
Erdélyi, T. and Saff, E. B., Riesz polarization in higher dimensions. J. Approx. Theory 171 2013, 128–147.CrossRefGoogle Scholar
Hardin, D. P., Kendall, A. P. and Saff, E. B., Polarization optimality of equally spaced points on the circle for discrete potentials. Discrete Comput. Geom. 50(2) 2013, 236–243.CrossRefGoogle Scholar
Khrushchev, S., Rational compacts and exposed quadratic irrationalities. J. Approx. Theory 159(2) 2009, 243–289.CrossRefGoogle Scholar