Article contents
NONCOMMUTATIVE REAL ALGEBRAIC GEOMETRY OF KAZHDAN’S PROPERTY (T)
Published online by Cambridge University Press: 30 July 2014
Abstract
It is well known that a finitely generated group  ${\rm\Gamma}$ has Kazhdan’s property (T) if and only if the Laplacian element
${\rm\Gamma}$ has Kazhdan’s property (T) if and only if the Laplacian element 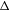 ${\rm\Delta}$ in
${\rm\Delta}$ in 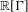 $\mathbb{R}[{\rm\Gamma}]$ has a spectral gap. In this paper, we prove that this phenomenon is witnessed in
$\mathbb{R}[{\rm\Gamma}]$ has a spectral gap. In this paper, we prove that this phenomenon is witnessed in 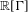 $\mathbb{R}[{\rm\Gamma}]$. Namely,
$\mathbb{R}[{\rm\Gamma}]$. Namely,  ${\rm\Gamma}$ has property (T) if and only if there exist a constant
${\rm\Gamma}$ has property (T) if and only if there exist a constant 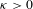 ${\it\kappa}>0$ and a finite sequence
${\it\kappa}>0$ and a finite sequence 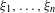 ${\it\xi}_{1},\ldots ,{\it\xi}_{n}$ in
${\it\xi}_{1},\ldots ,{\it\xi}_{n}$ in 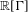 $\mathbb{R}[{\rm\Gamma}]$ such that
$\mathbb{R}[{\rm\Gamma}]$ such that 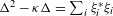 ${\rm\Delta}^{2}-{\it\kappa}{\rm\Delta}=\sum _{i}{\it\xi}_{i}^{\ast }{\it\xi}_{i}$. This result suggests the possibility of finding new examples of property (T) groups by solving equations in
${\rm\Delta}^{2}-{\it\kappa}{\rm\Delta}=\sum _{i}{\it\xi}_{i}^{\ast }{\it\xi}_{i}$. This result suggests the possibility of finding new examples of property (T) groups by solving equations in 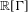 $\mathbb{R}[{\rm\Gamma}]$, possibly with the assistance of computers.
$\mathbb{R}[{\rm\Gamma}]$, possibly with the assistance of computers.
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 1 , January 2016 , pp. 85 - 90
- Copyright
- © Cambridge University Press 2014
References
- 11
- Cited by




