Article contents
The nub of an automorphism of a totally disconnected, locally compact group
Published online by Cambridge University Press: 23 January 2013
Abstract
To any automorphism,  $\alpha $, of a totally disconnected, locally compact group,
$\alpha $, of a totally disconnected, locally compact group, 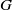 $G$, there is associated a compact,
$G$, there is associated a compact,  $\alpha $-stable subgroup of
$\alpha $-stable subgroup of 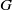 $G$, here called the nub of
$G$, here called the nub of  $\alpha $, on which the action of
$\alpha $, on which the action of  $\alpha $ is ergodic. Ergodic actions of automorphisms of compact groups have been studied extensively in topological dynamics and results obtained transfer, via the nub, to the study of automorphisms of general locally compact groups. A new proof that the contraction group of
$\alpha $ is ergodic. Ergodic actions of automorphisms of compact groups have been studied extensively in topological dynamics and results obtained transfer, via the nub, to the study of automorphisms of general locally compact groups. A new proof that the contraction group of  $\alpha $ is dense in the nub is given, but it is seen that the two-sided contraction group need not be dense. It is also shown that each pair
$\alpha $ is dense in the nub is given, but it is seen that the two-sided contraction group need not be dense. It is also shown that each pair 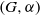 $(G, \alpha )$, with
$(G, \alpha )$, with 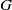 $G$ compact and
$G$ compact and  $\alpha $ ergodic, is an inverse limit of pairs that have ‘finite depth’ and that analogues of the Schreier refinement and Jordan–Hölder theorems hold for pairs with finite depth.
$\alpha $ ergodic, is an inverse limit of pairs that have ‘finite depth’ and that analogues of the Schreier refinement and Jordan–Hölder theorems hold for pairs with finite depth.
- Type
- Research Article
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 8
- Cited by




