No CrossRef data available.
Article contents
On the intersection of random rotations of a symmetric convex body
Published online by Cambridge University Press: 28 March 2014
Abstract
Let C be a symmetric convex body of volume 1 in 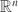 ${\mathbb R}^n$. We provide general estimates for the volume and the radius of C ∩ U(C) where U is a random orthogonal transformation of
${\mathbb R}^n$. We provide general estimates for the volume and the radius of C ∩ U(C) where U is a random orthogonal transformation of 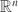 ${\mathbb R}^n$. In particular, we consider the case where C is in the isotropic position or C is the volume normalized Lq-centroid body Zq(μ) of an isotropic log-concave measure μ on
${\mathbb R}^n$. In particular, we consider the case where C is in the isotropic position or C is the volume normalized Lq-centroid body Zq(μ) of an isotropic log-concave measure μ on 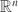 ${\mathbb R}^n$.
${\mathbb R}^n$.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 157 , Issue 1 , July 2014 , pp. 13 - 30
- Copyright
- Copyright © Cambridge Philosophical Society 2014
References
REFERENCES
[2]Bourgain, J.On the distribution of polynomials on high dimensional convex sets. Geom. Aspects of Funct. Analysis (Lindenstrauss-Milman eds.). Lecture Notes in Math. 1469 (1991), 127–137.Google Scholar
[3]Bourgain, J. and Milman, V. D.New volume ratio properties for convex symmetric bodies in  ${\mathbb R}^n$. Invent. Math. 88 (1987), 319–340.Google Scholar
${\mathbb R}^n$. Invent. Math. 88 (1987), 319–340.Google Scholar
[4]Brazitikos, S., Giannopoulos, A., Valettas, P. and Vritsiou, B-H.Geometry of isotropic convex bodies. Math. Surv. Monogr. (Amer. Math. Society) 196 (2014), 594.Google Scholar
[5]Cordero–Erausquin, D., Fradelizi, M. and Maurey, B.The (B)-conjecture for the Gaussian measure of dilates of symmetric convex sets and related problems. J. Funct. Anal. 214 (2004), 410–427.Google Scholar
[6]Fleury, B.Concentration in a thin Euclidean shell for log-concave measures. J. Funct. Anal. 259 (2010), 832–841.Google Scholar
[7]Fleury, B., Guédon, O. and Paouris, G.A stability result for mean width of $Lp$-centroid bodies. Adv. Math. 214, 2 (2007), 865–877.Google Scholar
[8]Giannopoulos, A., Milman, V. D. and Tsolomitis, A.Asymptotic formulas for the diameter of sections of symmetric convex bodies. J. Funct. Anal. 223 (2005), 86–108.Google Scholar
[9]Giannopoulos, A., Stavrakakis, P., Tsolomitis, A. and Vritsiou, B-H. Geometry of the $Lq$-centroid bodies of an isotropic log-concave measure. Trans. Amer. Math. Soc. (to appear).Google Scholar
[10]Gordon, Y.On Milman's inequality and random subspaces which escape through a mesh in  ${\mathbb R}^n$. Lecture Notes in Math. 1317 (1988), 84–106.Google Scholar
${\mathbb R}^n$. Lecture Notes in Math. 1317 (1988), 84–106.Google Scholar
[11]Guédon, O. and Milman, E.Interpolating thin-shell and sharp large-deviation estimates for isotropic log-concave measures. Geom. Funct. Anal. 21 (2011), 1043–1068.Google Scholar
[12]Kashin, B. S.Sections of some finite-dimensional sets and classes of smooth functions. Izv. Akad. Nauk. SSSR Ser. Mat. 41 (1977), 334–351.Google Scholar
[13]Klartag, B.On convex perturbations with a bounded isotropic constant. Geom. Funct. Anal. 16 (2006), 1274–1290.Google Scholar
[14]Klartag, B.A central limit theorem for convex sets. Invent. Math. 168 (2007), 91–131.CrossRefGoogle Scholar
[15]Klartag, B.Power-law estimates for the central limit theorem for convex sets. J. Funct. Anal. 245 (2007), 284–310.Google Scholar
[16]Klartag, B. and Milman, E.Centroid bodies and the logarithmic Laplace transform – a unified approach. J. Fun. Anal. 262 (2012), 10–34.Google Scholar
[17]Klartag, B. and Milman, E.Inner regularization of log-concave measures and small-ball estimates. Geom. Aspects of Funct. Analysis (Klartag-Mendelson-Milman eds.), Lecture Notes in Math. 2050 (2012), 267–278.Google Scholar
[18]Klartag, B. and Vershynin, R.Small ball probability and Dvoretzky theorem, Israel J. Math. 157 (2007), 193–207.Google Scholar
[19]Latała, R. and Oleszkiewicz, K.Small ball probability estimates in terms of widths. Studia Math. 169 (2005), 305–314.Google Scholar
[20]Litvak, A. E., Pajor, A. and Tomczak–Jaegermann, N.Diameters of sections and coverings of convex bodies. J. Funct. Anal. 231 (2006), 438–457.Google Scholar
[21]Milman, V. D.Geometrical inequalities and mixed volumes in the Local Theory of Banach spaces. Astérisque 131 (1985), 373–400.Google Scholar
[22]Milman, V. D.Random subspaces of proportional dimension of finite dimensional normed spaces: approach through the isoperimetric inequality. Lecture Notes in Math. 1166 (1985), 106–115.Google Scholar
[23]Milman, V. D.Isomorphic symmetrization and geometric inequalities. Lecture Notes in Math. 1317 (1988), 107–131.Google Scholar
[24]Milman, V. D.Some applications of duality relations. Lecture Notes in Math. 1469 (1991), 13–40.Google Scholar
[25]Milman, V. D. and Schechtman, G.Asymptotic Theory of Finite Dimensional Normed Spaces. Lecture Notes in Math. 1200, (Springer, Berlin, 1986).Google Scholar
[26]Milman, V. D. and Schechtman, G.Global versus Local asymptotic theories of finite-dimensional normed spaces. Duke Math. J. 90 (1997), 73–93.Google Scholar
[27]Pajor, A. and Tomczak–Jaegermann, N.Subspaces of small codimension of finite dimensional Banach spaces. Proc. Amer. Math. Soc. 97 (1986), 637–642.Google Scholar
[28]Paouris, G.Concentration of mass in convex bodies. Geom. Funct. Anal. 16 (2006), 1021–1049.Google Scholar
[29]Paouris, G.Small ball probability estimates for log-concave measures. Trans. Amer. Math. Soc. 364 (2012), 287–308.CrossRefGoogle Scholar
[30]Pisier, G.The volume of convex bodies and banach space geometry. Cambridge Tracts in Math. 94 (1989).Google Scholar
[31]Schneider, R.Convex Bodies: The Brunn–Minkowski Theory. Encyclopedia Math. Appl. 44, (Cambridge University Press, Cambridge, 1993).Google Scholar
[32]Szarek, S. J. and Tomczak–Jaegermann, N.On nearly Euclidean decompositions of some classes of Banach spaces, Comp. Math. 40 (1980), 367–385.Google Scholar
[33]Vershynin, R.Isoperimetry of waists and local versus global asymptotic convex geometries (with an appendix by M. Rudelson and R. Vershynin). Duke Math. J. 131 (2006), 1–16.Google Scholar




