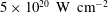1. Introduction
It has been known since the discovery of Maxwell’s equations that light, i.e., electromagnetic (EM) radiation, exerts a pressure on a reflecting object, and thus may accelerate it. In 1925, Zander[Reference Zander1] suggested exploiting the radiation pressure of the Sun for space travel using light sails, i.e., mirrors of large area and small thickness.
The scattering of an EM wave by a particle also leads to momentum absorption and acceleration. In 1957, Veksler[Reference Veksler2] suggested that Thomson scattering by a small cluster containing
![]() $N$
electrons may accelerate the cluster to high velocities. The fundamental point of Veksler’s proposal was that the radiation force on the cluster scaled as
$N$
electrons may accelerate the cluster to high velocities. The fundamental point of Veksler’s proposal was that the radiation force on the cluster scaled as
![]() $N^2$
, providing an example of his new principle of coherent acceleration, i.e., the use of collective effects to accelerate large amounts of particles to high energies.
$N^2$
, providing an example of his new principle of coherent acceleration, i.e., the use of collective effects to accelerate large amounts of particles to high energies.
After the invention of the laser, Forward in 1962[Reference Forward3, Reference Gilster4] and Marx in 1966[Reference Marx5] proposed using an Earth-based laser system to accelerate a rocket up to relativistic velocities. Marx’s paper included a relativistic analysis of the motion of a sail, i.e., a plane perfect mirror, accelerated by radiation pressure, based on the equations
where
![]() $I=I(t)$
is the intensity of the laser pulse,
$I=I(t)$
is the intensity of the laser pulse,
![]() $\sigma _0$
is the surface mass density of the sail, and
$\sigma _0$
is the surface mass density of the sail, and
![]() $\gamma =(1-V^2/c^2)^{-1/2}$
. The concept is sketched in Figure 1. The most interesting result (but also the subject of a long-lasting controversy[Reference Simmons and McInnes7]) was the expression for the mechanicalefficiency
$\gamma =(1-V^2/c^2)^{-1/2}$
. The concept is sketched in Figure 1. The most interesting result (but also the subject of a long-lasting controversy[Reference Simmons and McInnes7]) was the expression for the mechanicalefficiency
![]() $\eta =2\beta /(1+\beta )$
(with
$\eta =2\beta /(1+\beta )$
(with
![]() $\beta =V/c$
), which reaches 100% in the relativistic limit
$\beta =V/c$
), which reaches 100% in the relativistic limit
![]() $\beta \to 1$
. Equations (1), hereafter referred to as the light sail (LS) equations, have the same form as for the motion of the Thomson scattering particle[Reference Landau and Lifshitz8], evidencing the connection with Veksler’s proposed mechanism.
$\beta \to 1$
. Equations (1), hereafter referred to as the light sail (LS) equations, have the same form as for the motion of the Thomson scattering particle[Reference Landau and Lifshitz8], evidencing the connection with Veksler’s proposed mechanism.
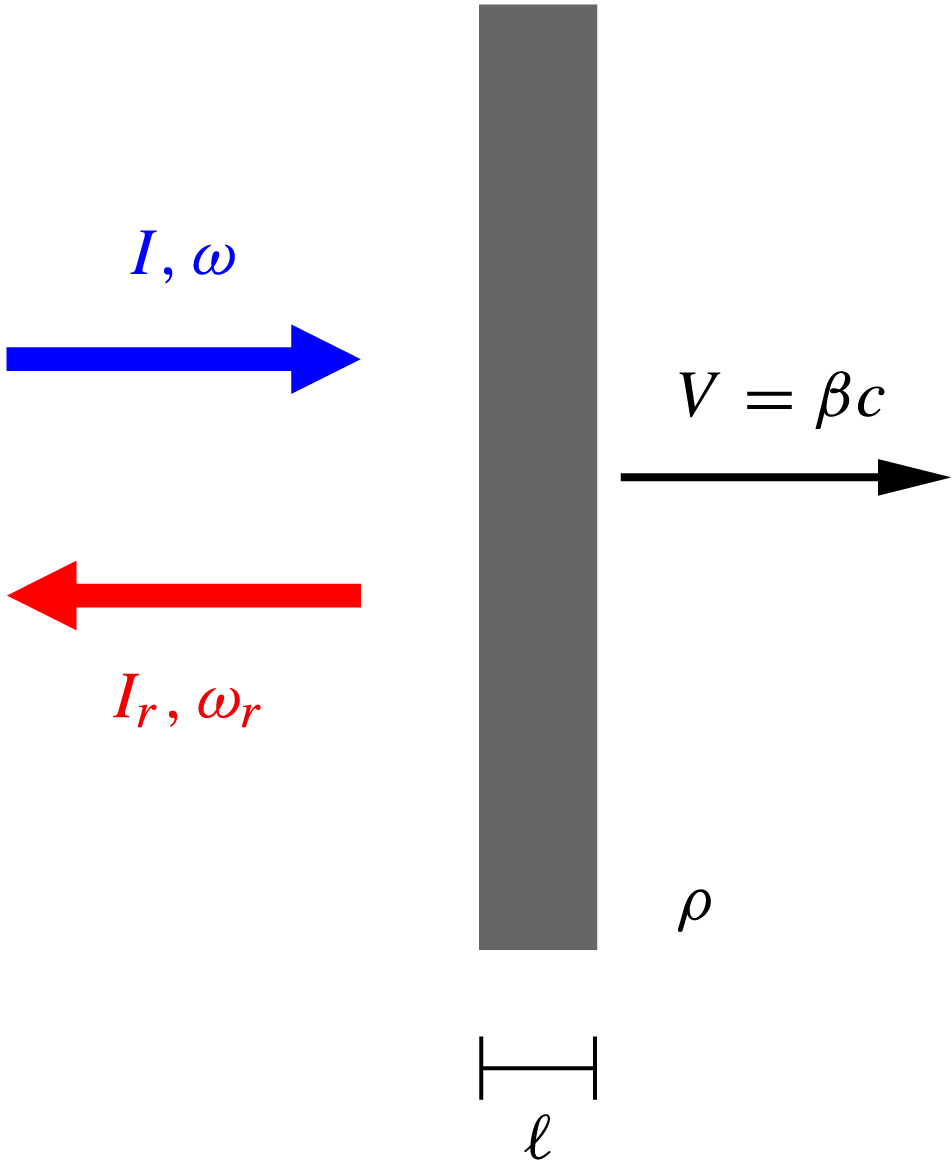
Figure 1. The light sail concept. The sail is modeled as a perfect mirror of surface density
![]() $\sigma =\rho \ell $
, with
$\sigma =\rho \ell $
, with
![]() $\rho $
the mass density and
$\rho $
the mass density and
![]() $\ell $
the thickness. The sail is pushed by a plane wave of intensity
$\ell $
the thickness. The sail is pushed by a plane wave of intensity
![]() $I$
and frequency
$I$
and frequency
![]() $\omega $
. Notice that the equations of motion for the sail given in (1) and the expression for the mechanical efficiency may be simply obtained by considering the Doppler shift of the reflected radiation [
$\omega $
. Notice that the equations of motion for the sail given in (1) and the expression for the mechanical efficiency may be simply obtained by considering the Doppler shift of the reflected radiation [
![]() $\omega _r=\omega (1-\beta )/(1+\beta )$
] and the conservation of the ‘number of photons’; see, for example, Ref. [Reference Macchi6].
$\omega _r=\omega (1-\beta )/(1+\beta )$
] and the conservation of the ‘number of photons’; see, for example, Ref. [Reference Macchi6].
In 2004, using particle-in-cell (PIC) simulations of the acceleration of a thin plasma foil by a laser pulse with intensity
![]() $I>10^{23}\ \mbox{W cm}^{-2}$
, Esirkepov et al.
[Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima9] showed that the motion of the foil was also well fitted by the above-mentioned equation, giving evidence that the foil was driven from radiation pressure. The scaling of the LS equations to foreseeable laser and target parameters showed the possibility of reaching the relativistic velocity of the foil, corresponding to an energy per nucleon above the GeV barrier. The coherent motion of the foil also implied an inherent mono-energetic spectrum, which would be crucial for most applications. Such features have then stimulated a strong interest in LS acceleration.
$I>10^{23}\ \mbox{W cm}^{-2}$
, Esirkepov et al.
[Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima9] showed that the motion of the foil was also well fitted by the above-mentioned equation, giving evidence that the foil was driven from radiation pressure. The scaling of the LS equations to foreseeable laser and target parameters showed the possibility of reaching the relativistic velocity of the foil, corresponding to an energy per nucleon above the GeV barrier. The coherent motion of the foil also implied an inherent mono-energetic spectrum, which would be crucial for most applications. Such features have then stimulated a strong interest in LS acceleration.
In this paper, we give a brief overview of the research on LS acceleration in the past decade, mostly focusing on theoretical aspects and open issues. A simple criterion for radiation pressure dominance at intensities around
![]() $5 \times 10^{20}\ \mbox{W cm}^{-2}$
is given, and the possibility for fast energy gain in the relativistic regime is pointed out. A more comprehensive presentation of experimental and simulation results may be found in recent review papers on laser-driven ion acceleration[Reference Daido, Nishiuchi and Pirozhkov10–Reference Fernandez, Albright, Beg, Foord, Hegelich, Honrubia, Roth, Stephens and Yin13].
$5 \times 10^{20}\ \mbox{W cm}^{-2}$
is given, and the possibility for fast energy gain in the relativistic regime is pointed out. A more comprehensive presentation of experimental and simulation results may be found in recent review papers on laser-driven ion acceleration[Reference Daido, Nishiuchi and Pirozhkov10–Reference Fernandez, Albright, Beg, Foord, Hegelich, Honrubia, Roth, Stephens and Yin13].
2. One-dimensional dynamics
For an arbitrary pulse profile
![]() $I(t)$
, the final value of
$I(t)$
, the final value of
![]() $\gamma $
is obtained from Equations (1) as
$\gamma $
is obtained from Equations (1) as
For a flat-top intensity profile, i.e., a constant value of
![]() $I$
between
$I$
between
![]() $t=0$
and
$t=0$
and
![]() $\tau _L$
, Equations (1) can be solved exactly. Here, we just give the limiting cases of
$\tau _L$
, Equations (1) can be solved exactly. Here, we just give the limiting cases of
![]() $\beta \ll 1$
and
$\beta \ll 1$
and
![]() $\beta \to 1$
, for which the integration is straightforward (notice that, for
$\beta \to 1$
, for which the integration is straightforward (notice that, for
![]() $\beta \simeq 1$
,
$\beta \simeq 1$
,
![]() $(1+\beta )/(1-\beta ) \simeq 4\gamma ^2$
):
$(1+\beta )/(1-\beta ) \simeq 4\gamma ^2$
):
where
![]() $\Omega =2I/\sigma _0 c^2$
. Equations (2) and (3) may be used to obtain the acceleration time and length in the laboratory for a given value of the final energy per nucleon
$\Omega =2I/\sigma _0 c^2$
. Equations (2) and (3) may be used to obtain the acceleration time and length in the laboratory for a given value of the final energy per nucleon
![]() ${\mathcal{E}}_{\max }=m_pc^2(\gamma _{\infty }-1)$
(notice that it would be incorrect to plug the pulse duration
${\mathcal{E}}_{\max }=m_pc^2(\gamma _{\infty }-1)$
(notice that it would be incorrect to plug the pulse duration
![]() $\tau _L$
in Equation (3) to obtain
$\tau _L$
in Equation (3) to obtain
![]() ${\mathcal{E}}_{\max }$
).
${\mathcal{E}}_{\max }$
).
It is evident that the energy gain is quite fast for
![]() $\beta \ll 1$
but becomes much slower in the relativistic regime as
$\beta \ll 1$
but becomes much slower in the relativistic regime as
![]() $\beta \to 1$
. In a realistic multi-dimensional scenario, this is a possible issue, because of laser pulse diffraction on distances larger than the Rayleigh length. Fortunately, as discussed below, the energy gain may be faster in three-dimensional (3D) geometry thanks to the target rarefaction.
$\beta \to 1$
. In a realistic multi-dimensional scenario, this is a possible issue, because of laser pulse diffraction on distances larger than the Rayleigh length. Fortunately, as discussed below, the energy gain may be faster in three-dimensional (3D) geometry thanks to the target rarefaction.
Obviously, the lighter the sail the higher the energy for a given laser pulse. However, if the foil target is too thin, then it becomes transparent to the laser pulse, and the radiation pressure boost drops down. Based on the simple model of a delta-like foil and purely transverse electron motion[Reference Vshivkov, Naumova, Pegoraro and Bulanov14, Reference Macchi15], the threshold for transparency due to relativistic effects is given by
where
![]() $a_0=(I/m_e n_cc^3)^{1/2}$
,
$a_0=(I/m_e n_cc^3)^{1/2}$
,
![]() $\zeta =\pi \sigma _0/(Zm_in_c\lambda )$
,
$\zeta =\pi \sigma _0/(Zm_in_c\lambda )$
,
![]() $n_c=\pi m_ec^2/(e^2\lambda ^2)=\pi /(r_c\lambda ^2)$
is the cut-off density, and
$n_c=\pi m_ec^2/(e^2\lambda ^2)=\pi /(r_c\lambda ^2)$
is the cut-off density, and
![]() $\lambda $
is the laser wavelength. Despite the very simplified underlying model, Equation (4) describes fairly well the onset of transparency and the breakdown of LS acceleration observed in 1D simulations[Reference Macchi, Veghini and Pegoraro16]. Actually, Equation (4) may be considered as slightly pessimistic, because, as the foil moves, the reflectivity increases, due to the decrease of the pulse frequency in the moving frame[Reference Macchi, Veghini, Liseykina and Pegoraro17]. The situation is more complex for finite-width pulses in multi-dimensional geometry, because the transverse expansion of the foil leads to a decrease of the surface density
$\lambda $
is the laser wavelength. Despite the very simplified underlying model, Equation (4) describes fairly well the onset of transparency and the breakdown of LS acceleration observed in 1D simulations[Reference Macchi, Veghini and Pegoraro16]. Actually, Equation (4) may be considered as slightly pessimistic, because, as the foil moves, the reflectivity increases, due to the decrease of the pulse frequency in the moving frame[Reference Macchi, Veghini, Liseykina and Pegoraro17]. The situation is more complex for finite-width pulses in multi-dimensional geometry, because the transverse expansion of the foil leads to a decrease of the surface density
![]() $\sigma $
in time.
$\sigma $
in time.
The above modeling considers the sail as a neutral rigid body with electrons comoving with ions. Indeed, charge separation effects are crucial in the ‘inner’ dynamics of LS acceleration. Figure 2 shows the initial stages of ion acceleration. Electrons are pushed into the target by the secular ponderomotive force per unit volume
![]() ${\bf f}_p=\left \langle {\bf J}\times {\bf B} \right \rangle $
, where the brackets denote a cycle average. The ponderomotive force sweeps and piles up the electrons, creating a charge depletion layer until
${\bf f}_p=\left \langle {\bf J}\times {\bf B} \right \rangle $
, where the brackets denote a cycle average. The ponderomotive force sweeps and piles up the electrons, creating a charge depletion layer until
![]() ${f}_p$
is exactly balanced by an electrostatic field
${f}_p$
is exactly balanced by an electrostatic field
![]() $E_x$
(this corresponds to the balance between
$E_x$
(this corresponds to the balance between
![]() $P_{\mathrm{rad}}$
and the electrostatic pressure on ions; see, for example, Refs. [Reference Macchi, Veghini and Pegoraro16, Reference Macchi, Veghini, Liseykina and Pegoraro17]). In turn,
$P_{\mathrm{rad}}$
and the electrostatic pressure on ions; see, for example, Refs. [Reference Macchi, Veghini and Pegoraro16, Reference Macchi, Veghini, Liseykina and Pegoraro17]). In turn,
![]() $E_x$
accelerates the ions as shown in Figure 1. In a first stage, the ions in the layer where the EM field penetrates are accelerated up to a velocity
$E_x$
accelerates the ions as shown in Figure 1. In a first stage, the ions in the layer where the EM field penetrates are accelerated up to a velocity
![]() $v_i$
within a time
$v_i$
within a time
![]() $t_c$
, given by[Reference Macchi, Cattani, Liseykina and Cornolti18]
$t_c$
, given by[Reference Macchi, Cattani, Liseykina and Cornolti18]
 $$\begin{eqnarray} \begin{array}{c} \frac {\upsilon _i}{c} \simeq \left (\frac {I}{\rho c^3}\right )^{1/2}= \left (\frac {Zm_en_c}{Am_pn_e}\right )^{1/2}a_0 , \\[1pc] t_c \simeq \frac {1}{\omega a_0}\left (\frac {Am_p}{Zm_e}\right )^{1/2}, \end{array}\label {eq:ionmotion} \end{eqnarray}$$
$$\begin{eqnarray} \begin{array}{c} \frac {\upsilon _i}{c} \simeq \left (\frac {I}{\rho c^3}\right )^{1/2}= \left (\frac {Zm_en_c}{Am_pn_e}\right )^{1/2}a_0 , \\[1pc] t_c \simeq \frac {1}{\omega a_0}\left (\frac {Am_p}{Zm_e}\right )^{1/2}, \end{array}\label {eq:ionmotion} \end{eqnarray}$$
where
![]() $\rho $
is the mass density (for simplicity we assume non-relativistic motion; see [Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei19] for relativistically corrected expressions). At
$\rho $
is the mass density (for simplicity we assume non-relativistic motion; see [Reference Robinson, Gibbon, Zepf, Kar, Evans and Bellei19] for relativistically corrected expressions). At
![]() $t=t_c$
, the accelerated ions have piled up at the position
$t=t_c$
, the accelerated ions have piled up at the position
![]() $x=x_s\simeq \upsilon _it_c$
. If this position coincides with the rear surface of the foil, the acceleration cycle may be repeated, and eventually the sequence of acceleration stages converges to the motion described by (1)[Reference Grech, Skupin, Diaw, Schlegel and Tikhonchuk20].
$x=x_s\simeq \upsilon _it_c$
. If this position coincides with the rear surface of the foil, the acceleration cycle may be repeated, and eventually the sequence of acceleration stages converges to the motion described by (1)[Reference Grech, Skupin, Diaw, Schlegel and Tikhonchuk20].
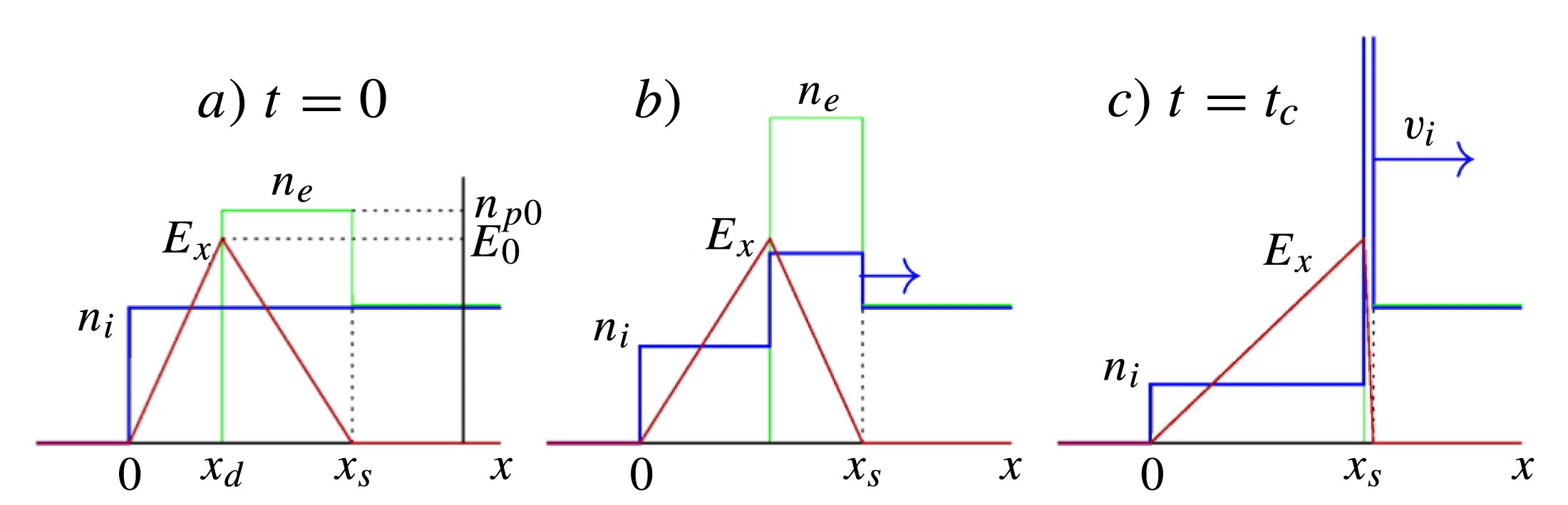
Figure 2. The first stage of ion acceleration driven by radiation pressure[Reference Macchi, Cattani, Liseykina and Cornolti18]. The densities of ions (
![]() $n_i$
) and electrons (
$n_i$
) and electrons (
![]() $n_e$
) are approximated by step-like functions. Ions initially in the
$n_e$
) are approximated by step-like functions. Ions initially in the
![]() $x_d<x<x_s$
layer are accelerated by the charge separation field
$x_d<x<x_s$
layer are accelerated by the charge separation field
![]() $E_x$
up to velocity
$E_x$
up to velocity
![]() $\upsilon _i$
at time
$\upsilon _i$
at time
![]() $t=t_c$
.
$t=t_c$
.
The correct balance of electrostatic and radiation pressure shows that only a fraction
![]() $F \simeq 1-a_0/\zeta $
of the ions is accelerated coherently as a sail, even if the motion of the latter is still described by Equation (1) with
$F \simeq 1-a_0/\zeta $
of the ions is accelerated coherently as a sail, even if the motion of the latter is still described by Equation (1) with
![]() $\sigma _0$
including the total mass of the foil[Reference Macchi, Veghini and Pegoraro16, Reference Macchi, Veghini, Liseykina and Pegoraro17]. During the motion, as long as the geometry is one dimensional, the electrostatic pressure on the sail depends only on the total charge behind the sail, while the radiation pressure decreases by a factor
$\sigma _0$
including the total mass of the foil[Reference Macchi, Veghini and Pegoraro16, Reference Macchi, Veghini, Liseykina and Pegoraro17]. During the motion, as long as the geometry is one dimensional, the electrostatic pressure on the sail depends only on the total charge behind the sail, while the radiation pressure decreases by a factor
![]() $(1-\beta )/(1+\beta )$
. Thus, to maintain the pressure balance, additional ions are progressively trapped in the sail[Reference Macchi, Veghini, Liseykina and Pegoraro17, Reference Eliasson, Liu, Shao, Sagdeev and Shukla21]. Applying the pressure balance as in Ref. [Reference Macchi, Veghini and Pegoraro16] with the velocity correction yields the final fraction of accelerated ions:
$(1-\beta )/(1+\beta )$
. Thus, to maintain the pressure balance, additional ions are progressively trapped in the sail[Reference Macchi, Veghini, Liseykina and Pegoraro17, Reference Eliasson, Liu, Shao, Sagdeev and Shukla21]. Applying the pressure balance as in Ref. [Reference Macchi, Veghini and Pegoraro16] with the velocity correction yields the final fraction of accelerated ions:
where
![]() $\beta _{\infty } = [(1+\mathcal{F})^{2}-1]/[(1+\mathcal{F})^2+1]$
. This shows that all ions are eventually accelerated in the relativistic limit.
$\beta _{\infty } = [(1+\mathcal{F})^{2}-1]/[(1+\mathcal{F})^2+1]$
. This shows that all ions are eventually accelerated in the relativistic limit.
3. Radiation pressure dominance
Since a thin plasma foil is not a perfect mirror, it is not trivial that irradiation by intense light should result in LS acceleration. In most accessible laser–plasma interaction conditions, strong heating of electrons occurs, and the resulting kinetic pressure exceeds the radiation pressure; in such a situation, the plasma foil expands and the resulting ion energy spectrum is very different from the LS case. The situation is somewhat reminiscent of the Crookes radiometer or light mill, where the vanes are white (reflecting) on one side and black (absorbing) on the other side: the mill rotates in the direction opposite to what would be expected from radiation pressure being higher on the white side than on the black side, because the effects of heating and thermal pressure dominate.
To find the conditions in which the radiation pressure
![]() $P_{\mathrm{ rad}}$
will dominate the acceleration, let us briefly recall the heating dynamics of electrons. At normal incidence, electrons are driven in the direction perpendicular to the target surface by the
$P_{\mathrm{ rad}}$
will dominate the acceleration, let us briefly recall the heating dynamics of electrons. At normal incidence, electrons are driven in the direction perpendicular to the target surface by the
![]() ${\bf v}\times {\bf B}$
force, which for linear polarization (LP) has an oscillating term at
${\bf v}\times {\bf B}$
force, which for linear polarization (LP) has an oscillating term at
![]() $2\omega $
(where
$2\omega $
(where
![]() $\omega $
is the laser frequency) in addition to the secular ponderomotive force. Heating of electrons occurs via oscillations across the laser–plasma interface driven by the oscillating term, which vanishes for circular polarization (CP)[Reference Macchi, Cattani, Liseykina and Cornolti18]. The use of CP pulses has then been proposed by several authors[Reference Zhang, Shen, Li, Jin and Wang22–Reference Robinson, Zepf, Kar, Evans and Bellei24] to obtain an efficient LS regime at ‘any’ intensity. Detailed 3D simulations in the relativistic regime[Reference Tamburini, Liseykina, Pegoraro and Macchi25] also showed that for CP pulses higher energies and better collimation of the ion beam are obtained with respect to LP pulses. Experiments performed so far, however, have shown a limited impact of the use of CP[Reference Henig, Steinke, Schnürer, Sokollik, Hörlein, Kiefer, Jung, Schreiber, Hegelich, Yan, Meyer ter Vehn, Tajima, Nickles, Sandner and Habs26–Reference Aurand, Kuschel, Jaeckel, Roedel, Zhao, Herzer, Paz, Bierbach, Polz, Elkin, Paulus, Karmakar, Gibbon, Kuehl and Kaluza29] and non-LS effects such as species separation in the spectrum[Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely, Osterholz, Prasad, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi28–Reference Steinke, Hilz, Schnürer, Priebe, Bränzel, Abicht, Kiefer, Kreuzer, Ostermayr, Schreiber, Andreev, Yu, Pukhov and Sandner30] (in the ideal LS regime, all species move at the same velocity; thus the energy per nucleon is independent on the mass number). These data suggest that tight focusing of the laser pulse and, possibly, imperfect conversion to CP may prevent efficient LS operation, at least in the intensity regime investigated so far, i.e.,
$\omega $
is the laser frequency) in addition to the secular ponderomotive force. Heating of electrons occurs via oscillations across the laser–plasma interface driven by the oscillating term, which vanishes for circular polarization (CP)[Reference Macchi, Cattani, Liseykina and Cornolti18]. The use of CP pulses has then been proposed by several authors[Reference Zhang, Shen, Li, Jin and Wang22–Reference Robinson, Zepf, Kar, Evans and Bellei24] to obtain an efficient LS regime at ‘any’ intensity. Detailed 3D simulations in the relativistic regime[Reference Tamburini, Liseykina, Pegoraro and Macchi25] also showed that for CP pulses higher energies and better collimation of the ion beam are obtained with respect to LP pulses. Experiments performed so far, however, have shown a limited impact of the use of CP[Reference Henig, Steinke, Schnürer, Sokollik, Hörlein, Kiefer, Jung, Schreiber, Hegelich, Yan, Meyer ter Vehn, Tajima, Nickles, Sandner and Habs26–Reference Aurand, Kuschel, Jaeckel, Roedel, Zhao, Herzer, Paz, Bierbach, Polz, Elkin, Paulus, Karmakar, Gibbon, Kuehl and Kaluza29] and non-LS effects such as species separation in the spectrum[Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely, Osterholz, Prasad, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi28–Reference Steinke, Hilz, Schnürer, Priebe, Bränzel, Abicht, Kiefer, Kreuzer, Ostermayr, Schreiber, Andreev, Yu, Pukhov and Sandner30] (in the ideal LS regime, all species move at the same velocity; thus the energy per nucleon is independent on the mass number). These data suggest that tight focusing of the laser pulse and, possibly, imperfect conversion to CP may prevent efficient LS operation, at least in the intensity regime investigated so far, i.e.,
![]() $I \simeq (2\times 10^{18}\div 2 \times 10^{21})\ \mbox{W cm}^{-2}$
.
$I \simeq (2\times 10^{18}\div 2 \times 10^{21})\ \mbox{W cm}^{-2}$
.
In view of future experiments at higher intensities and of possible technical difficulties for producing ultraintense CP pulses, it appears important to discuss possible conditions for radiation pressure dominance also for LP, when electron heating is important. Heuristically, the transfer of energy to ions via
![]() $P_{\mathrm{ rad}}$
can be efficient if it is ‘faster’ than the heating of electrons, which occurs on a laser halfcycle. Esirkepov et al.
[Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima9] suggested that ions should become promptly relativistic, i.e., reaching a velocity close to
$P_{\mathrm{ rad}}$
can be efficient if it is ‘faster’ than the heating of electrons, which occurs on a laser halfcycle. Esirkepov et al.
[Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima9] suggested that ions should become promptly relativistic, i.e., reaching a velocity close to
![]() $c$
within one cycle, so that they would ‘stick’ to electrons. To estimate the corresponding laser intensity for such a regime, let us assume
$c$
within one cycle, so that they would ‘stick’ to electrons. To estimate the corresponding laser intensity for such a regime, let us assume
![]() $\upsilon _i \simeq c/2$
in Equation (5): this gives
$\upsilon _i \simeq c/2$
in Equation (5): this gives
which for
![]() $n_e/n_c \simeq 100$
gives
$n_e/n_c \simeq 100$
gives
![]() $I\lambda ^2> 10^{23}\ \mbox{W cm}^{-2}\ \mu \mbox{m}^2$
, which is the typical intensity of the simulations in Ref. [Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima9]. These values are not currently available, although they may be reached in the laboratory within the next decade.
$I\lambda ^2> 10^{23}\ \mbox{W cm}^{-2}\ \mu \mbox{m}^2$
, which is the typical intensity of the simulations in Ref. [Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima9]. These values are not currently available, although they may be reached in the laboratory within the next decade.
Here, we propose a different condition, which leads to a more accessible intensity threshold. The above-defined ion acceleration time
![]() $t_c$
may be taken as the relevant temporal scale for energy transfer to ions. For electrons, acceleration occurs on a laser halfcycle being driven by the oscillating force at
$t_c$
may be taken as the relevant temporal scale for energy transfer to ions. For electrons, acceleration occurs on a laser halfcycle being driven by the oscillating force at
![]() $2\omega $
. Thus we suggest
$2\omega $
. Thus we suggest
![]() $t_c<\pi /\omega $
as the condition for energy transfer to ions being more efficient than to electrons. This leads to the threshold for the laser amplitude
$t_c<\pi /\omega $
as the condition for energy transfer to ions being more efficient than to electrons. This leads to the threshold for the laser amplitude
which is equivalent to
![]() $I\lambda ^2>5 \times 10^{20}\ \mbox{W cm}^{-2}\ \mu \mbox{m}^2$
, independently of the plasma density. This estimate is in qualitative agreement with LS signatures being observed in current experiments at similar intensities[Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely, Osterholz, Prasad, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi28]. A slightly greater intensity threshold of
$I\lambda ^2>5 \times 10^{20}\ \mbox{W cm}^{-2}\ \mu \mbox{m}^2$
, independently of the plasma density. This estimate is in qualitative agreement with LS signatures being observed in current experiments at similar intensities[Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely, Osterholz, Prasad, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi28]. A slightly greater intensity threshold of
![]() $10^{21}\ \mbox{W cm}^{-2}\ \mu \mbox{m}^2$
has been suggested by Qiao et al.
[Reference Qiao, Kar, Geissler, Gibbon, Zepf and Borghesi31] on a different basis, i.e., by comparing the ion energy gain due to the radiation pressure push with that in the fast electron sheath.
$10^{21}\ \mbox{W cm}^{-2}\ \mu \mbox{m}^2$
has been suggested by Qiao et al.
[Reference Qiao, Kar, Geissler, Gibbon, Zepf and Borghesi31] on a different basis, i.e., by comparing the ion energy gain due to the radiation pressure push with that in the fast electron sheath.
4. Fast gain regimes: ‘unlimited’ acceleration
In a realistic situation, the laser pulse has a finite width, and it drives a cocoon deformation and transverse expansion of the target. This unavoidable effect may lead to early breakthrough of the laser pulse and termination of the LS stage; thus the use of a smooth transverse profile to keep a nearly plane geometry was suggested by several simulation studies. In contrast, Bulanov et al. [Reference Bulanov, Echkina, Esirkepov, Inovenkov, Kando, Pegoraro and Korn32] suggested that the decrease of target density due to transverse expansion may lead, in proper conditions, to acceleration up to higher energies than in the planar case, at the expense of the number of accelerated ions. This has been named the ‘unlimited’ acceleration regime.
In the following, we give a brief and simplified account of the detailed theory developed by Bulanov et al. [Reference Bulanov, Echkina, Esirkepov, Inovenkov, Kando, Pegoraro and Korn33]. The basic modification of Equation (1) for the longitudinal motion of the sail is that the surface density now depends on time due to the transverse expansion,
where
![]() $\Lambda (t)$
describes the dilatation of the transverse position of a fluid element of the sail, i.e.,
$\Lambda (t)$
describes the dilatation of the transverse position of a fluid element of the sail, i.e.,
![]() $r_{\perp }(t)=\Lambda (t)r_{\perp }(0)$
, and
$r_{\perp }(t)=\Lambda (t)r_{\perp }(0)$
, and
![]() $D$
is the dimensionality of the system;
$D$
is the dimensionality of the system;
![]() $D=1$
corresponds to planar geometry (constant
$D=1$
corresponds to planar geometry (constant
![]() $\sigma $
),
$\sigma $
),
![]() $D=2$
to two-dimensional Cartesian geometry, and
$D=2$
to two-dimensional Cartesian geometry, and
![]() $D=3$
to three-dimensional geometry with cylindrical symmetry. Now, it is assumed that for a given element the motion is ballistic after an initial kick by the laser pulse delivering a transverse momentum
$D=3$
to three-dimensional geometry with cylindrical symmetry. Now, it is assumed that for a given element the motion is ballistic after an initial kick by the laser pulse delivering a transverse momentum
![]() $p_{\perp }=m_i\varpi _0r_{\perp }(0)$
, i.e., proportional to the initial position. This relation might be justified by observing that such kick comes from the transverse ponderomotive force, which is proportional to the gradient of the intensity and thus would be a linear function of position for a parabolic profile. It is further assumed that
$p_{\perp }=m_i\varpi _0r_{\perp }(0)$
, i.e., proportional to the initial position. This relation might be justified by observing that such kick comes from the transverse ponderomotive force, which is proportional to the gradient of the intensity and thus would be a linear function of position for a parabolic profile. It is further assumed that
![]() $p_{\perp } \ll p_{\parallel }$
, with
$p_{\perp } \ll p_{\parallel }$
, with
![]() $p_{\parallel }$
the longitudinal momentum. The transverse velocity thus decreases as a result of the increasing longitudinal momentum. This leads to the equation for
$p_{\parallel }$
the longitudinal momentum. The transverse velocity thus decreases as a result of the increasing longitudinal momentum. This leads to the equation for
![]() $\Lambda $
,
$\Lambda $
,
with the coupled equation for
![]() $p_{\parallel }=\gamma \beta _{\parallel }$
:
$p_{\parallel }=\gamma \beta _{\parallel }$
:
For further simplification, we consider the asymptotic ultrarelativistic limit, in which
![]() $\beta _{\parallel }\to 1$
and
$\beta _{\parallel }\to 1$
and
![]() $({1-\beta _{\parallel }})/({1+\beta _{\parallel }}) \simeq (2\gamma )^{-2}$
. In this limit, we find a solution
$({1-\beta _{\parallel }})/({1+\beta _{\parallel }}) \simeq (2\gamma )^{-2}$
. In this limit, we find a solution
with the time constants given for
![]() $D=1,2,3$
by
$D=1,2,3$
by
 $$\begin{eqnarray} \begin{array}{c} \tau _{1/3}=\left (\frac {3}{4\Omega }\right ) , \quad \tau _{2/4}=\left (\frac {1}{\Omega \varpi _0}\right )^{1/2} , \\[1pc] \tau _{3/5}=\left (\frac {48}{125\Omega \varpi _0^2}\right )^{1/3} . \end{array} \end{eqnarray}$$
$$\begin{eqnarray} \begin{array}{c} \tau _{1/3}=\left (\frac {3}{4\Omega }\right ) , \quad \tau _{2/4}=\left (\frac {1}{\Omega \varpi _0}\right )^{1/2} , \\[1pc] \tau _{3/5}=\left (\frac {48}{125\Omega \varpi _0^2}\right )^{1/3} . \end{array} \end{eqnarray}$$
Fast energy gain in this regime thus depends on the initial conditions via the parameter
![]() $\varpi _0$
. Assuming the initial transverse kick to be of the same order as the longitudinal one,
$\varpi _0$
. Assuming the initial transverse kick to be of the same order as the longitudinal one,
![]() $\varpi _0\simeq \Omega $
may be assumed for a quick estimate. For a given temporal profile
$\varpi _0\simeq \Omega $
may be assumed for a quick estimate. For a given temporal profile
![]() $I(t)$
, the final energy and surface density along the axis may be obtained by integrating Equations (10) and (11) with respect to the proper time
$I(t)$
, the final energy and surface density along the axis may be obtained by integrating Equations (10) and (11) with respect to the proper time
![]() $t'=t-X/c$
, with
$t'=t-X/c$
, with
![]() ${\mathrm{d}}t'=(1-\beta _{\parallel }){\mathrm{d}}t$
. Bulanov et al.
[Reference Bulanov, Echkina, Esirkepov, Inovenkov, Kando, Pegoraro and Korn33] also discuss ‘optimal’ pulse profiles to maximize the acceleration; heuristically, since the ‘unlimited’ mechanism is actually limited by the onset of transparency, one argues that the decrease of the density may be matched with the decrease of the pulse frequency in the sail frame to keep a constant reflectivity.
${\mathrm{d}}t'=(1-\beta _{\parallel }){\mathrm{d}}t$
. Bulanov et al.
[Reference Bulanov, Echkina, Esirkepov, Inovenkov, Kando, Pegoraro and Korn33] also discuss ‘optimal’ pulse profiles to maximize the acceleration; heuristically, since the ‘unlimited’ mechanism is actually limited by the onset of transparency, one argues that the decrease of the density may be matched with the decrease of the pulse frequency in the sail frame to keep a constant reflectivity.
5. 3D simulations
The above-outlined theory shows that, differently from other acceleration mechanisms[Reference Sgattoni, Londrillo, Macchi and Passoni34, Reference d’Humières, Brantov, Bychenkov and Tikhonchuk35], the energy gain may be higher in a realistic 3D geometry that with respect to a 1D plane case. Confirmation of this theory in numerical experiments thus requires fully 3D large-scale simulations, which are feasible on the most powerful present-day parallel supercomputers.
Simulations by Tamburini et al.
[Reference Tamburini, Liseykina, Pegoraro and Macchi25] (Figure 3(a)) have given a first evidence of the energy enhancement in fully 3D simulations. These simulations also indicated a baseline for LS operation in the relativistic regime, showing that the use of CP leads to higher energies and a more collimated beam with respect to the LP case, and also to negligible radiation friction effects. To evaluate the energy gain at the end of the acceleration stage, larger computational resources have been necessary to extend the simulation time by four times. In such simulations, the temporal dependence of maximum ion energy is in good agreement with the
![]() ${\sim } t^{3/5}$
scaling given by Equation (12), as shown in Figure 3(b))[Reference Macchi, Sgattoni, Sinigardi, Borghesi and Passoni12]. Ultimately, the acceleration is stopped by the onset of transparency. These simulations have been performed on the FERMI supercomputer at CINECA, Italy.
${\sim } t^{3/5}$
scaling given by Equation (12), as shown in Figure 3(b))[Reference Macchi, Sgattoni, Sinigardi, Borghesi and Passoni12]. Ultimately, the acceleration is stopped by the onset of transparency. These simulations have been performed on the FERMI supercomputer at CINECA, Italy.

Figure 3. 3D particle-in-cell simulations of thin foil acceleration. (a) Space and energy distribution of ions[Reference Tamburini, Liseykina, Pegoraro and Macchi25] (reproduced by permission of APS) at
![]() $t=20T$
from the acceleration start (
$t=20T$
from the acceleration start (
![]() $T=2\pi /\omega $
laser period). (b) Maximum ion energy versus time[Reference Macchi, Sgattoni, Sinigardi, Borghesi and Passoni12] (reproduced by permission of IOP Publishing). Both simulations have been performed for a
$T=2\pi /\omega $
laser period). (b) Maximum ion energy versus time[Reference Macchi, Sgattoni, Sinigardi, Borghesi and Passoni12] (reproduced by permission of IOP Publishing). Both simulations have been performed for a
![]() $9\lambda \times (10\lambda )^2$
pulse (FWHM values) with peak amplitude
$9\lambda \times (10\lambda )^2$
pulse (FWHM values) with peak amplitude
![]() $a_0=198$
and circular polarization, and a hydrogen plasma foil with surface density
$a_0=198$
and circular polarization, and a hydrogen plasma foil with surface density
![]() $\sigma =64m_pn_c\lambda $
, so that
$\sigma =64m_pn_c\lambda $
, so that
![]() $a_0\simeq \zeta $
. See the references for details.
$a_0\simeq \zeta $
. See the references for details.
6. Conclusions and perspectives
The laser-driven light sail concept, which was first studied as a visionary approach to interstellar travel, currently represents an implementation of Veksler’s coherent acceleration paradigm and a possible route towards a laser–plasma accelerator. Experiments are just entering the regime of intensities exceeding
![]() $5\times 10^{20}\ \mbox{W cm}^{-2}$
where, according to our discussion, the radiation pressure push is expected to be the dominant acceleration mechanism. Recent progress in both achieving extremely high-contrast pulses and manufacturing ultrathin targets has been crucial for light sail experiments[Reference Henig, Steinke, Schnürer, Sokollik, Hörlein, Kiefer, Jung, Schreiber, Hegelich, Yan, Meyer ter Vehn, Tajima, Nickles, Sandner and Habs26–Reference Steinke, Hilz, Schnürer, Priebe, Bränzel, Abicht, Kiefer, Kreuzer, Ostermayr, Schreiber, Andreev, Yu, Pukhov and Sandner30], and results such as the observation of the fast scaling of ion energy in the non-relativistic limit[Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely, Osterholz, Prasad, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi28] are promising. However, several open issues are apparent, such as achieving mono-energetic spectra, and the effect of parameters such as the laser pulse focusing and duration still needs to be completely understood and optimized.
$5\times 10^{20}\ \mbox{W cm}^{-2}$
where, according to our discussion, the radiation pressure push is expected to be the dominant acceleration mechanism. Recent progress in both achieving extremely high-contrast pulses and manufacturing ultrathin targets has been crucial for light sail experiments[Reference Henig, Steinke, Schnürer, Sokollik, Hörlein, Kiefer, Jung, Schreiber, Hegelich, Yan, Meyer ter Vehn, Tajima, Nickles, Sandner and Habs26–Reference Steinke, Hilz, Schnürer, Priebe, Bränzel, Abicht, Kiefer, Kreuzer, Ostermayr, Schreiber, Andreev, Yu, Pukhov and Sandner30], and results such as the observation of the fast scaling of ion energy in the non-relativistic limit[Reference Kar, Kakolee, Qiao, Macchi, Cerchez, Doria, Geissler, McKenna, Neely, Osterholz, Prasad, Quinn, Ramakrishna, Sarri, Willi, Yuan, Zepf and Borghesi28] are promising. However, several open issues are apparent, such as achieving mono-energetic spectra, and the effect of parameters such as the laser pulse focusing and duration still needs to be completely understood and optimized.
With the availability of next-generation lasers at extreme intensities, success of the light sail approach in producing relativistic ions will depend on the possibility of achieving and controlling the so-called ‘unlimited’ regime based on a suitable (and possibly self-regulated) transverse expansion of the target. On this route one expects technical challenges, such as clean circular polarization for ultraintense pulses, as well as other possible issues not considered in this paper, such as the target stability.
Acknowledgements
It is a pleasure to thank S. V. Bulanov and F. Pegoraro for scientific inspiration and enlightening discussions, and T. V. Liseykina, A. Sgattoni, S. Sinigardi, and M. Tamburini for hard simulation work. Support from the Italian Ministry of University and Research via the FIR project ‘SULDIS’ is acknowledged.