Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-17T18:40:33.561Z Has data issue: false hasContentIssue false
  • English
  • Français

Geostrophic adjustment with gyroscopic waves: stably neutrally stratified fluid without the traditional approximation

Published online by Cambridge University Press:  23 April 2014

G. M. Reznik
G. M. Reznik*
Affiliation:
P. P. Shirshov Institute of Oceanology, Russian Academy of Sciences, 36, Nakhimovskiy Prospekt, 117997, Moscow, Russia
*
†Email address for correspondence: greznikmd@yahoo.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine nonlinear geostrophic adjustment in a rapidly rotating (small Rossby number Ro) stably neutrally stratified (SNS) fluid consisting of a stratified upper layer with 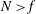$N>f$ (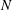$N$ is the buoyancy frequency, 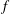$f$ the Coriolis parameter) and a homogeneous lower layer, the density and other fields being continuous at the interface between the layers. The angular speed of rotation is non-parallel to gravity; the traditional and hydrostatic approximations are not used. The wave spectrum in the model consists of internal and gyroscopic waves. During the adjustment an arbitrary long-wave perturbation is split in a unique way into slow quasi-geostrophic (QG) and fast ageostrophic components with typical time scales 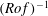$(Ro\, f)^{-1}$ and 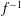$f^{-1}$, respectively. The QG flow is governed by two coupled nonlinear equations of conservation of QG potential vorticity (PV) in the layers. The fast component is a sum of internal waves and inertial oscillations (long gyroscopic waves) confined to the homogeneous layer and modulated by an amplitude depending on coordinates and slow time. On times 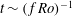$t\sim (\, f\, Ro)^{-1}$ the slow component is not influenced by the fast one but the inertial oscillations amplitude is coupled to the QG flow and obeys an equation practically coinciding with that in the barotropic case (Reznik, J. Fluid Mech., vol. 743, 2014, pp. 585–605). A non-stationary boundary layer with large vertical gradients of horizontal velocity develops in the stratified layer near the interface to prevent penetration of the inertial oscillations into the stratified fluid; an analogous weaker boundary layer arises near the upper rigid lid. At large times the internal waves gradually decay because of dispersion and the resulting motion consists of the slow QG component and inertial oscillations confined to the barotropic lower layer.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 747 , 25 May 2014 , pp. 605 - 634
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Badulin, S. I., Vasilenko, V. M. & Yaremchuk, M. I. 1991 Interpretation of quasi-inertial motions using Megapoligon data as an example. Izv. Atmos. Ocean. Phys. 27, 446–452.Google Scholar
Brekhovskikh, L. M. & Goncharov, V. 1994 Mechanics of Continua and Wave Dynamics, 342 pp. Springer.Google Scholar
Gerkema, T. & Shrira, V. I. 2005 Near-inertial waves in the ocean: beyond the traditional approximation. J. Fluid Mech. 529, 195–219.Google Scholar
Gerkema, T., Zimmerman, J. T. F., Maas, L. R. M. & van Haren, H. 2008 Geophysical and astrophysical fluid dynamics beyond the ‘traditional approximation’. Rev. Geophys. 46, RG2004.Google Scholar
van Haren, H. & Millot, C. 2005 Gyroscopic waves in the Mediterranean Sea. Geophys. Res. Lett. 32, L24614.CrossRefGoogle Scholar
Il’in, A. M. 1970 Asymptotic properties of a solution of a boundary-value problem. Math. Notes 8, 625–632.Google Scholar
Il’in, A. M. 1972 On the behaviour of the solution of a boundary-value problem when $t\to \infty $ . Math. USSR, Sb. 16, 545–572.Google Scholar
Kamenkovich, V. M. 1977 Fundamentals of Ocean Dynamics, 249 pp. Elsevier.Google Scholar
Kamenkovich, V. M. & Kamenkovich, I. V. 1993 On the evolution of Rossby waves, generated by wind stress in a closed basin, incorporating total mass conservation. Dyn. Atmos. Oceans 18, 67–103.Google Scholar
Kamke, E. 1976 Handbook of Ordinary Differential Equations. Chelsea.Google Scholar
Kasahara, A. 2003 The roles of the horizontal component of the Earth’s angular velocity in nonhydrostatic linear models. J. Atmos. Sci. 60, 1085–1095.Google Scholar
Kochin, N. E., Kibel, L. A. & Rose, N. V. 1964 Theoretical Hydromechanics. Wiley-Interscience.Google Scholar
LeBlond, P. H. & Mysak, L. A. 1978 Waves in the Ocean, 602 pp. Elsevier.Google Scholar
Miropol’sky, Y. Z. 2001 Dynamics of Internal Gravity Waves in the Ocean, 406 pp. Kluwer.Google Scholar
Pedlosky, J. 1979 Geophysical Fluid Dynamics, 624 pp. Springer.Google Scholar
Reznik, G. M. 2013 Linear dynamics of a stably-neutrally stratified ocean. J. Mar. Res. 71 (4), 253–288.Google Scholar
Reznik, G. M. 2014 Geostrophic adjustment with gyroscopic waves: barotropic fluid without traditional approximation. J. Fluid Mech. 743, 585–605.Google Scholar
Reznik, G. M., Zeitlin, V. & Ben Jelloul, M. 2001 Nonlinear theory of geostrophic adjustment. Part 1. Rotating shallow-water model. J. Fluid Mech. 445, 93–120.Google Scholar
Sedov, L. I. 1997 Mechanics of Continuous Media, Series in Theoretical and Applied Mechanics, vol. 4. 1368 pp. World Scientific.Google Scholar
Shrira, V. I. & Townsend, W. A. 2010 Inertia-gravity waves beyond the inertial latitude. Part 1. Inviscid singular focusing. J. Fluid Mech. 664, 478–509.Google Scholar
Shrira, V. I. & Townsend, W. A. 2013 Near-inertial waves and deep ocean mixing. Phys. Scr. T155, 1–12.Google Scholar
Timmermans, M. L., Melling, H. & Rainville, L. 2007 Dynamics in the Deep Canada Basin, Arctic Ocean, inferred by thermistor chain time series. J. Phys. Oceanogr. 37, 1066–1076.CrossRefGoogle Scholar
Young, W. R. & Ben Jelloul, M. 1997 Propagation of near-inertial oscillations through a geostrophic flow. J. Mar. Res. 55, 735–766.Google Scholar
Zeitlin, V., Reznik, G. M. & Ben Jelloul, M. 2003 Nonlinear theory of geostrophic adjustment. Part 2. Two-layer and continuously stratified primitive equations. J. Fluid Mech. 491, 207–228.Google Scholar